Chaos frees the Universe

Chaos seems to provide a bridge between the deterministic laws of physics and the laws of chance, implying that the Universe is genuinely creative and that the notion of free will is real

Paul Davies

All science is founded on the assumption that the physical world is ordered. The most powerful expression of this order is found in the laws of physics. Nobody knows where these laws come from, nor why they apparently operate universally and unfailingly, but we see them at work all around us: in the rhythm of night and day, the pattern of planetary motions, the regular ticking of a clock.

The ordered dependability of nature is not however, ubiquitous. The vagaries of the weather, the devastation of an earthquake, or the fall of a meteorite seem to be arbitrary and fortuitous. Small wonder that our ancestors attributed these events to the moodiness of the gods. But how are we to reconcile these apparently random "acts of God" with the supposed underlying lawfulness of the Universe?

The ancient Greek philosophers regarded the world as a battleground between the forces of order, producing cosmos, and those of disorder,which led to chaos. They believed that random or disordering processes were negative, evil influences. Today, we don't regard the role of chance in nature as malicious, merely as blind. A chance event may act constructively, as in biological evolution, or destructively, such as when an aircraft fails from metal fatigue.

Though individual chance events may give the impression of lawlessness, disorderly processes, as a whole, may still display statistical regularities. Indeed, casino managers put as much faith in the laws of chance as engineers put in the laws of physics. But this raises something of a paradox. How can the same physical processes obey both the laws of physics and the laws of chance?

Following the formulation of the laws of mechanics by Isaac Newton in the 17th century, scientists became accustomed to thinking of the Universe as a gigantic mechanism. The most extreme form of this doctrine was strikingly expounded by Pierre Simon de Laplace in the 19th century. He envisaged every particle of matter as unswervingly locked in the embrace of strict mathematical laws of motion. These laws dictated the behaviour of even the smallest atom in the most minute detail. Laplace argued that, given the state of the Universe at any one instant, the entire cosmic future would be uniquely fixed, to infinite precision, by Newton's laws.

The concept of the Universe as a strictly deterministic machine governed by eternal laws profoundly influenced the scientific world view, standing as it did in stark contrast to the old Aristotelian picture of the cosmos as a living organism. A machine can have no "free will"; its future is rigidly determined from the beginning of time. Indeed, time ceases to have much physical significance in this picture, for the future is already contained in the present. As Ilya Prigogine, a theoretical chemist at the University of Brussels, has eloquently expressed it, God is reduced to a mere archivist, turning the pages of a cosmic history book that is already written.

Implicit in this somewhat bleak mechanistic picture was the belief that there are actually no truly chance processes in nature. Events may appear to us to be random but, it was reasoned, this could be attributed to human ignorance about the details of the processes concerned. Take, for example, Brownian motion. A tiny particle suspended in a fluid can be observed to execute a haphazard zigzag movement as a result of the slightly uneven buffeting it suffers at the hands of the hands of the fluid molecules that bombard it.Brownian motion is the archetypical random, unpredictable process. Yet, so the argument ran, if we could follow in detail the activities of all the individual molecules involved, Brownian motion would be every bit as predictable and deterministic as clockwork. The apparently random motion of the Brownian particle is attributed solely to the lack of information about the myriads of participating molecules, arising from the fact that our senses are too coarse to permit detailed observation at the molecular level.

For a while, it was commonly believed that apparently "chance" events were always the result of our ignoring, or effectively averaging over, vast numbers of hidden variables, or degrees of freedom. The toss of a coin or a die, the spin of a roulette wheel-these would no longer appear random if we could observe the world at the molecular level. The slavish conformity of the cosmic machine ensured that lawfulness was folded up in even the most haphazard events, albeit in an awesomely convoluted tangle.

Two major developments of the 20th century have, however, put paid to the idea of a clockwork universe. First there was quantum mechanics. At the heart of quantum physics lies Heisenberg's uncertainty principle, which states that everything we can measure is subject to truly random fluctuations. Quantum fluctuations are not the result of human limitations or hidden degrees of freedom; they are inherent in the workings of nature on an atomic scale. For example, the exact moment of decay of a particular radioactive nucleus is intrinsically uncertain. An element of genuine unpredictability is thus injected into nature.

Despite the uncertainty principle, there remains a sense in which quantum mechanics is still a deterministic theory. Although the outcome of a particular quantum process might be undetermined, the relative probabilities of different outcomes evolve in a deterministic manner. What this means is that you cannot know in any particular case what will be the outcome of the "throw of the quantum dice" but you can know completely accurately how the betting odds vary from moment to moment. As a statistical theory, quantum mechanics remains deterministic. Quantum physics thus builds chance into the very fabric of reality, but a vestige of the Newtonian-Laplacian world view remains.

Along came chaos
Then along came chaos. As the previous articles in this series have discussed, the essential ideas of chaos were already present in the work of the mathematician Henri Poincaré at the turn of the century, but it is only in recent years, especially with the advent of fast electronic computers, that people have appreciated the full significance of chaos theory.

The key feature of a chaotic process concerns the way that predictive errors evolve with time. Let me first give an example of a non-chaotic system: the motion of a simple pendulum. Imagine two identical pendulums swinging in exact synchronism. Suppose that one pendulum is slightly disturbed so that its motion gets a little out of step with the other pendulum. This discrepancy, or phase shift, remains small as the pendulums go on swinging.

Faced the task of predicting the motion of a simple pendulum, one could measure the position and velocity of the bob at some instant, and use Newton's laws to compute the subsequent behaviour. Any error in the initial measurement propagates through the calculation and appears as an error in the prediction. For the simple pendulum, a small input error implies a small output error in the predictive computation. In a typical non-chaotic system, errors accumulate with time. Crucially, though, the errors grow only in proportion to the time (or perhaps a small power thereof), so they remain relatively manageable.

Now let me contrast this property with that of a chaotic system. Here a small starting difference between two identical systems will rapidly grow. In fact, the hallmark of chaos is that the motions diverge exponentially fast. Translated into a prediction problem, this means that any input error multiplies itself at an escalating rate as a function of prediction time, so that before long it engulfs the calculation, and all predictive power is lost. Small input errors thus swell to calculation-wrecking size in very short order.

The distinction between chaotic and non-chaotic behaviour is well illustrated by the case of the spherical pendulum, this being a pendulum free to swing in two directions (see New Scientist, "Chaos in the swing of a pendulum", 24 July 1986). In practice, this could be a ball suspended on the end of a string. If the system is driven in a plane by a periodic motion applied at the pivot, it will start to swing about. After a while, it may settle into a stable and entirely predictable pattern of motion, in which the bob traces out an elliptical path with the driving frequency. However, if you alter the driving frequency slightly, this regular motion may give way to chaos, with the bob swinging this way and then that, doing a few clockwise turns, then a few anticlockwise turns in an apparently random manner.

The randomness of this system does not arise from the effect of myriads of hidden degrees of freedom. Indeed, by modelling mathematically only the three observed degrees of freedom (the three possible directions of motions), one may show that the behaviour of the pendulum is nonetheless random. And this is in spite of the fact that the mathematical model concerned is strictly deterministic.

It used to be supposed that determinism went hand in hand with predictability, but we can now see that this need not be the case. A deterministic system is one in which future states are completely determined, through some dynamical law, by preceding states. There is thus a one-to-one association between earlier and later states. In computational terms, this suggests a one-to-one association between the input and the output of a predictive calculation. But now we must remember that any predictive computation will contain some because we cannot measure physical quantities to unlimited precision. Moreover, computers can handle only finite quantities of data anyway.

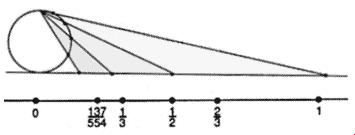The situation is represented geometrically in Figure above. The fan of straight lines establishes a one-to-one correspondence between points on the arc of the circle and points on the horizontal line. In the idealised case of perfect geometrical forms consisting of infinitesimally thin continuous lines and points of zero size, this correspondence is meaningful. But no real geometrical forms can be like this. As the top of the circle is approached, so points from a smaller and smaller arc are associated with a bigger and bigger segment of the horizontal line. (Think of points near the top of the arc as analogous to the initial conditions of a chaotic system, and points towards the right of the horizontal line as predicted values at later and later times.) The slightest uncertainty about one's position on the arc leads to a huge uncertainty about the corresponding point on the line segment. De one-to-one association becomes smudged into meaninglessness.

We might call this the fiction of the real line. The Ancient Greeks realised that points on a line could be labelled by numbers, according to their distance from one end. The Figure above shows a segment from 0 to 1. Fractions, such as 2/3 and 137/554, could be used to label the points in between. The Greeks called these numbers "rational" (as in ratio). By using enough digits in the numerators and denominators we can choose a fraction that marks a place arbitrarily close to any designated point on the line. Nevertheless, it is readily shown that continuous line segments cannot have all their points labelled this way. That requires not only all possible rational numbers, but all irrational numbers too. An irrational number cannot be expressed as one whole number divided by another. It may instead be expressed as a decimal, with an infinite number of digits.

The set of all rational and irrational numbers form what mathematicians call the real numbers, and they underlie almost all modern theories of physics. The very notion of continuous mechanical processes, epitomised by Newton's calculus which he formulated to describe them, is rooted in the concept of real numbers. Some real numbers, such as 1/2 = 0.5 or 1/3 = 0.3333..., can be expressed compactly. But a typical real number has a decimal expansion consisting of an infinite string of digits with no systematic pattern to it, in other words, it is a random sequence (New Scientist, "A random walk in arithmetic", 24 March 1990). It follows that to specify such a number involves an infinite quantity of information. This is clearly impossible, even in principle. Even if we were to commandeer the entire observable Universe and employ it as a digital computer, its information storage capacity would be finite. Thus, the notion of a continuous line described by real numbers is exposed as a mathematical fiction.

Now consider the consequences for a chaotic system. Determinism implies predictability only in the idealised limit of infinite precision. In the case of the pendulum, for example, the behaviour will be determined uniquely by the initial conditions. The initial data includes the position of the bob, so exact predictability demands that we must assign the real number to the position that correctly describes the distance of the bob 's centre from a fixed point- And this infinite precision is, as we have seen, impossible.

In a non-chaotic system this limitation is not so serious because the errors expand only slowly. But in a chaotic system errors grow at an accelerating rate. Suppose there is an uncertainty in, say, the fifth significant figure, and that this affects the prediction of how the system is behaving after a time, t. A more accurate analysis might reduce the uncertainty to the tenth significant figure. But the exponential nature of error growth implies that the uncertainty now manifests itself after a time 2t. So a hundred-thousand-fold improvement in initial accuracy achieves a mere doubling of the predictability span. It is this "sensitivity to initial conditions" that leads to well-known statements about the flapping of butterflies' wings in the Amazonian jungle causing a tornado in Texas.

Chaos evidently provides us with a bridge between the laws of physics and the laws of chance. In a sense, chance or random events can indeed always be traced to ignorance about details, but whereas Brownian motion appears random because of the enormous number of degrees of freedom we are voluntarily overlooking, deterministic chaos appears random because we are necessarily ignorant of the ultra-fine detail of just a few degrees of freedom. And whereas Brownian chaos is complicated because the molecular bombardment is itself a complicated process, the motion of, say, the spherical pendulum is complicated even though the system itself is very simple. Thus, complicated behaviour does not necessarily imply complicated forces or laws. So the study of chaos has revealed how it is possible to reconcile the complexity of a physical world displaying haphazard and capricious behaviour with the order and simplicity of underlying laws of nature.

Though the existence of deterministic chaos comes as a surprise, we should not forget that nature is not, in fact, deterministic anyway. The indeterminism associated with quantum effects will intrude into the dynamics of all systems, chaotic or otherwise, at the atomic level. It might be supposed that quantum uncertainty would combine with chaos to amplify the unpredictability of the Universe. Curiously, however, quantum mechanics seems to have a subduing effect on chaos (New Scientist, "Quantum physics on the edge of chaos", 19 November 1987). A number of model systems that are chaotic at the classical level are found to be non-chaotic when quantised. At this stage, the experts are divided about whether quantum chaos is possible, or how it would show itself if it did exist. Though the topic will undoubtedly prove important for atomic and molecular physics, it is of little relevance to the behaviour of macroscopic objects, or to the Universe as a whole. What can we conclude about Laplace's image of a clockwork universe? The physical world contains a wide range of both chaotic and non-chaotic systems. Those that are chaotic have severely limited predictability, and even one such system would rapidly exhaust the entire Universe's capacity to compute its behaviour. It seems, then, that the Universe is incapable of digitally computing the future behaviour of even a small part of itself, let alone all of itself. Expressed more dramatically, the Universe is its own fastest simulator.

This conclusion is surely profound. It means that, even accepting a strictly deterministic account of nature, the future states of the Universe are in some sense "open". Some people have seized on this openness to argue for the reality of human free will. Others claim that it bestows upon nature an element of creativity, an ability to bring forth that which is genuinely new, something not already implicit in earlier states of the Universe, save in the idealised fiction of the real numbers. Whatever the merits of such sweeping claims, it seems safe to conclude from the study of chaos that the future of the Universe is not irredeemably fixed. To paraphrase Prigogine, the final chapter of the great cosmic book has yet to be written.

Paul Davis is professor of mathematical physics at the University of Adelaide, and author of The Cosmic Blueprint. This is the last feature in the New Scientist series on chaos. The series will be published as a book next year.

Further Reading Autonomy of Free will and Determinism with a view to the Ontological Interpretation of Quantum Physics - Iraj Jafarian PhD