Mastering Chaos

It is now possible to control some systems that behave. Engineers can use chaos to stabilize lasers, chaotically electronic circuits and even the hearts of animals

by William L . Ditto and Louis M. Pecora

WILLIAM L.DITTO and LOUIS M. PECORA have pioneered methods for controlling the chaotic behavior of mechanical, electrical and biological systems. Ditto is assistant professor of physics at the Georgia Institute of Technology. He won the Office of Naval Research Young Investigator Award. Ditto and his collaborators were the first to control chaos in an experimental system. Since 1977 Pecora has been a research physicist at the U.S. Naval Research Laboratory and now heads a program in nonlinear dynamics in solid-state systems there. Pecora is in the process of patenting four devices that exploit chaos.

What good is chaos? Some would say it is unreliable, uncontrollable and therefore unusable. Indeed, no one can ever predict exactly how a chaotic system will behave over long periods. For that reason, engineers have typically dealt with chaos in just one way: they have avoided it. We find that strategy somewhat shortsighted. Within the past few years we and our colleagues have demonstrated that chaos is manageable, exploitable and even invaluable.

Chaos has already been applied to increase the power of lasers, synchronize the output of electronic circuits, control oscillations in chemical reactions, stabilize the erratic beat of unhealthy animal hearts and encode electronic messages for secure communications. We anticipate that in the near future engineers will no longer shun chaos but will embrace it.

In this time sequence,computed streamlines show how blood flows through the heart's mitral valve.

There are at least two reasons why chaos is so useful. First, the behavior of a chaotic system is a collection of many orderly behaviors, none of which dominates under ordinary circumstances. In recent years, investigators have shown that by perturbing a chaotic system in the right way, they can encourage the system to follow one of its many regular behaviors. Chaotic systems are unusually flexible because they can rapidly switch among many different behaviors.

SUDDEN DEATH One night in 1991, 26-year-old James Graham-Rowe died suddenly. There was no warning. He was generally fit and healthy. The coroner was so perplexed he ordered three post-mortems and eventually called James's parents to apologise for his failure to find a cause for their son's death. Twelve years later, the evidence suggests that James suffered from a genetic disease that affects the electrical activity of the heart but leaves the organ itself looking perfectly healthy. The first symptom of this condition is often the last: the heart simply stops beating properly. Scientists suspect that Brugada syndrome, as it is called, could be jeopardising clinical trails of a host of new drugs. It may even be behind some cases of cot deaths. [New Scientist]

Second, although chaos is unpredictable, it is deterministic. If two nearly identical chaotic systems of the appropriate type are impelled, or driven, by the same signal, they will produce the same output, even though no one can say what that output might be see "The Amateur Scientist," page 101].This phenomenon has already made possible a variety of interesting technologies for communications.

For more than a century, chaos has been studied almost exclusively by a few theoreticians, and they must be credited for developing some of the concepts on which all applications are based. Most natural systems are nonlinear : a change in behavior is not a simple function of a change in conditions. Chaos is one type of nonlinear behavior.The distinguishing feature of chaotic systems is that they exhibit a sensitivity to initial conditions. To be more specific, if two chaotic systems that are nearly identical are in two slightly different states, they will rapidly evolve toward very different states.

To the casual observer, chaotic systems appear to behave in a random fashion. Yet close examination shows that they have an underlying order. To visualize dynamics in any system, the Irish-born physicist William Hamilton and the German mathematician Karl Jacobi and their contemporaries devised, more than 150 years ago, one of the fundamental concepts necessary for understanding nonlinear dynamics: the notion of state space.

Any chaotic system that can be described by a mathematical equation includes two kinds of variables: dynamic and static. Dynamic variables are the fundamental quantities that are changing all the time. For a chaotic mechanism, the dynamic variables might be the position of a moving part and its velocity. Static variables, which might also be called parameters, are set at some point but then are never changed. The static variable of a chaotic mechanism might be the length of some part or the speed of a motor.

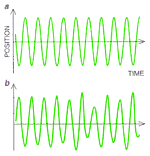
METALLIC RIBBON sways chaotically in a magnetic field whose strength fluctuates periodically. Recent advances make it possible to control such chaotic motions. The ribbon is made of a material whose stiffness depends on the strength of the field. The magnetic field changes at a rate of around one cycle per second. A strobelight flashes at the same frequency so that long-exposure photography captures the irregularities in be motion of the ribbon. A computer system analyzes the movement of the ribbon using a scheme developed by theorists at be University of Maryland. By making slight changes to the field, the computer system can transform the chaotic motions (top) to periodic oscillations of almost any frequency (bottom).

State space is essentially a graph in which each axis is associated with one dynamic variable. A point in state space represents the state of the system at a given time. As the system changes, it moves from point to point in state space, defining a trajectory, or curve. This trajectory represents the history of the dynamic system.

Chaotic systems have complicated trajectories in state space. In contrast, linear systems have simple trajectories, such as loops [see box on page 64]. Yet the trajectory of a chaotic system is not random ; it passes through certain regions of state space while avoiding , others. The trajectory is drawn toward a so-called chaotic attractor, which in some sense is the very essence of a chaotic system. The chaotic attractor is the manifestation of the fixed parameters and equations that determine the values of the dynamic variables.

So if one measures the trajectory of a chaotic system, one cannot predict where it will be on the attractor at some point in the distant future. The chaotic attractor, on the other hand, remains the same no matter when one measures it. Once researchers have obtained information about the chaotic attractor of a system, they can begin to use chaos to their advantage.

In 1989 one of us (Pecora) discovered that a chaotic system could be built in such a way that its parts would act in perfect synchrony. As is well known, isolated chaotic systems cannot synchronize. If one could construct two chaotic systems that were virtually identical but separate, they would quickly fall out of step with each other because any slight difference between the two systems would be magnified. In some cases, however, the parts of a system can be arranged so that they exhibit identical chaotic behavior. In fact, these parts can be located at great distances from one another, making it possible to use synchronized chaos for communications.

To build a chaotic system whose parts are synchronous, one needs to understand the concept of stability. A system is stable if, when perturbed somewhat, its trajectory through state space changes only a little from what it might have been otherwise. The Russian mathematician Aleksandr M. Lyapunov realized that a single number could be used to represent the change caused by a perturbation. He divided the size of the perturbation at one instant in time by its size a moment before. He then performed the same computation at various intervals and averaged the results.

This quantity, now known as the Lyapunov multiplier, describes how much, on average, a perturbation will change. If the Lyapunov multiplier is less than one, the perturbations die out, and the system is stable. If the multiplier is greater than one, however, the disturbances grow, and the system is unstable. All chaotic systems have a Lyapunov multiplier greater than one and so are always unstable. This is the root of the unpredictability of chaos.

The parts of a chaotic system must be stable if they are to be synchronized. This does not mean that the entire system cannot be chaotic. If two similar, stable parts are driven by the same chaotic signal, they will both seem to exhibit chaotic behavior, but they will suppress rather than magnify any differences between them, thereby creating an opportunity for synchronized chaos.

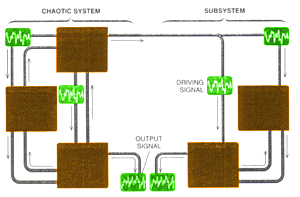
One design developed by Pecora and Thomas L. Carroll of the U.S. Naval Research Laboratory uses a subsystem of an ordinary chaotic system as the synchronizing mechanism. They first distinguished the synchronizing subsystem from other supporting parts and then duplicated the synchronizing subsystems [see illustrations on opposite page]. The supporting subsystem then supplied a driving signal for the original synchronizing subsystem and its duplicate.

If the synchronizing subsystems have Lyapunov multipliers that are less than one, that is, if these subsystems are stable, they will behave chaotically but will be in complete synchrony. The stability of the subsystems guarantees that any small perturbations will be damped out, and therefore the synchronizing subsystems will react to the signals from the supporting subsystem in practically the same way, no matter how complex the signals are.

To demonstrate synchronized chaos initially, Pecora created a computer simulation based on the chaotic Lorenz system, which is named after American meteorologist Edward N. Lorenz, who in 1963 discovered chaotic behavior in a computer study of the weather. The Lorenz system has three dynamic variables, and consequently the state-space picture of such systems is three-dimensional. Plotting the trajectory of the Lorenz system in state space reveals what is known as the Lorenz chaotic attractor [see "Chaos," by James P. Crutchfield, J. Doyne Farmer, Norman H. Packard and Robert S. Shaw; SCIENTIFIC AMERICAN, December 1986].

For the computer simulation. Pecora started with the three dynamic variables of the Lorenz system and chose one of them as the driving signal. The subsystem consisting of the two remaining dynamic variables was then duplicated. Although the subsystem and its duplicate were initially set up to produce different outputs, they quickly converged, generating chaotic signals in synchrony. In state space the two subsystems began at different points, caught up to each other and waltzed about on their chaotic attractors in a synchronized ballet.

Representing Chaos Conventionally, the motion of an object is represented as a "time series," a graph showing the change in position over time. Chaotic motions, however, can often be more conveniently visualized in "state space," a plot of the history of the changing variables, which are typically the position and velocity of the object. Consider, for example, the motion of the ball in the mechanism shown at the right (a). The ball is attached to a spring that gets stiffer as it is stretched or compressed. (In technical terms, the spring delivers a nonlinear restoring force.) As the board moves cyclically back and forth, the spring is pushed and pulled and causes the ball to move. Hence, the movement of the ball ultimately depends on the force with which the spring is pushed. If the force is weak, the ball moves in a simple trajectory, which repeats with each cycle of the force from the board (b). The state-space path (c) shows all the Information about the motion of the ball at each instant of time. Because the motion is periodic, the path will retrace itself with each board cycle. The state space reveals a so-called period-one attractor. The same kind of behavior would be observed if the ball were attached to an ordinary (linear) spring. The interesting behavior occurs as the driving force on the spring is increased. At a certain point, the ball can be made to move back and forth in a more complicated way for each oscillation of the board. Hence, the time series and state-space path change (d, e). Specifically, the previous period-one orbit becomes unstable, and the system produces a period-two attractor, that is, it takes two board cycles before the path retraces itself. If the force on the spring increases past some threshold, the ball moves chaotically. No pattern is apparent in the time series (f). The state space, on the other hand, reveals a chaotic attractor (g): the state-space path never retraces itself, yet it occupies only certain regions of state space. Indeed, a chaotic attractor can be considered a combination of unstable periodic orbits.

Until this discovery, scientists had no reason to believe that the stability of a subsystem could be independent of the stability of the rest of the system. Nor had anyone thought that a nonlinear system could be stable when driven with a chaotic signal.

Stability depends not only on the properties of the subsystem itself but on the driving signal. A subsystem may be stable when driven by one type of chaotic signal but not when driven by another. The trick is to find those subsystems that react to a chaotic signal in a stable way. In some cases, the stability of a subsystem can be estimated using a mathematical model, but in general such predictions are difficult.

Investigators have only begun to experiment with synchronized chaos. In 1989 Carroll built the first synchronized chaos circuit. By duplicating part of a circuit that exhibited chaotic behavior, he created a circuit in which the subsystem and its duplicate were driven by the same chaotic signal.These two subsystems generated voltages that fluctuated in a truly chaotic fashion but were always in step with each other.

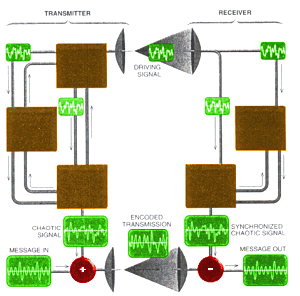
Carroll realized that his synchronized chaos circuit might be used for a private communications system. For example, imagine that Bill wants to send a secret message to Al. Bill has a device that generates a chaotic drive signal, and he has a subsystem that reacts to the signal in a stable way. Al has a copy of the subsystem. Bill translates his secret message into an electronic signal and combines it with the chaotic output of his subsystem. Bill then transmits the encoded message as well as the drive signal.

Anyone who intercepts these signals will detect only chaotic noise and will be unable to extract any information (unless, of course, he or she manages to get a copy of Bill's or Al's subsystem). When Al receives the drive signal , he sends it through his subsystem, which reproduces the chaotic output of Bill's subsystem. Al can then subtract this output from the encoded information signal to recover the secret message.

It is rather easy, as Carroll has demonstrated, to recover signals buried in chaos. To build a practical, secure communications system, however, engineers will probably need to develop sophisticated schemes in which the encoding process involves more than just adding chaos to message signals.

CHAOTIC SIGNALS produced by a system and a subsystem can be generated in complete synchrony. The important feature of the system is that the blue and green components are stable when driven by the chaotic signals from the red part. In other words, small changes in the initial settings of be blue and green parts have little or no effect on the behavior they eventually settle into. The subsystem consists of duplicates of the blue and green components of be system. Although the red, blue and green parts of the system send signals to one another, there is no feedback between be red component and the subsystem.

PRIVATE COMMUNICATIONS can be achieved using the scheme for synchronized chaos [see upper illustration on this page]. The transmitter adds a chaotic signal to a message signal; it then broadcasts be encoded signal and a drive signal. The drive signal is sent to two components in be receiver, causing them to generate a chaotic signal in synchrony with be signal produced in the transmitter. The chaotic signal is then subtracted from the encoded signal to yield the original information.

Researchers at the Massachusetts Institute of Technology, Washington State University and the University of California at Berkeley are building new combinations of chaotic subsystems for signal processing and communications. We have also continued our work and found a chaotic system that performs the same operations as a phase-locked loop-a device that, among other things, allows an FM radio receiver to track the changes in the transmitted signal.

Carroll and Pecora had such success with using chaotic signals to drive stable parts of chaotic systems that they suspected there might be an advantage to employing chaotic signals to drive stable periodic systems. Their intuition led them to another series of promising applications. Imagine two systems that are driven by the same periodic signal and  have the same nonchaotic period-two attractor. The term "period two" means that in two periods of the driving signal, the system travels around the attractor once. If two such systems are driven with the same signal but are initially at opposite ends of the attractor, they will cycle around the attractor and never catch up to each other. In other words, if the two systems start out of phase, they will remain out of phase forever.

By changing the periodic driving signal to a certain type of chaotic signal, workers have recently discovered that two systems can be coaxed to operate in phase. Yet not all types of chaotic signals will perform this task. Some such signals may cause the system themselves to behave chaotically, thereby eliminating any chance of getting them in phase. Engineers must therefore figure out what type of chaotic signal to use for each kind of system.

A good first choice is the signal produced by a system originally invented by Otto E.Rössler. The Rössler signal is nearly periodic and resembles a sine wave whose amplitude and wavelength have been randomized somewhat from one cycle to the next. Such signals, which have come to be known as pseudoperiodic, can be made, in general, simply by taking a periodic signal and adding chaos to it. If several identical systems whose attractors are all period two or greater are driven by the appropriate pseudoperiodic signal, they will all get in step.

This application was first demonstrated by Carroll in 1990. He built a set of electronic circuits that had period-two attractors and drove them with one of several pseudoperiodic signals, including the Rössler type. In each case, he found he was able to solve the out-of-step problem. Yet the circuits did get out of phase for short periods. That occurred because it is impossible to build several circuits that are exactly the same. Nevertheless, it is quite feasible to keep the circuits in phase 90 percent of the time.

Whereas some investigators have searched for uses of chaos, others have sought to control it. One key to this effort lies in the realization that a chaotic attractor is an infinite collection of unstable periodic behaviors. The easiest way to illustrate this point is to consider a system consisting of a weight, a "nonlinear" spring and a motor. One end of the spring hangs from the motor; the other is attached to the weight. The motor lifts the spring up and down with a force that can be adjusted. The dynamic variables of the system are the position of the weight and its velocity, and these define the state space. If the driving force of the motor is weak, the weight will move up and down once for each cycle of the motor. At the same time, the weight speeds up and slows down, and therefore the trajectory in state space is a single loop, or what is technically called a period-one orbit.

If the driving force of the motor is increased somewhat, the period-one orbit becomes an unstable behavior, and the weight will move up and down once for every two cycles of the motor. In state space the trajectory is now a double loop, or period-two orbit. If the driving force is increased again, the period-two orbit becomes unstable, and a period-four orbit will emerge. Indeed, if the driving force is sufficiently strong, all periodic orbits become unstable, and a chaotic attractor will appear. In a rigorous sense, the chaotic attractor is an ensemble of unstable periodic orbits.

Four years ago Edward Ott, Celso Grebogi and James A. Yorke of the University of Maryland developed a scheme in which a chaotic system can be encouraged to follow one particular unstable orbit through state space. The scheme can therefore take advantage of the vast array of possible behaviors that make up the chaotic system.

The method devised by Ott, Grebogi and Yorke (referred to as OGY ) is conceptually straightforward. To start, one obtains information about the chaotic system by analyzing a slice of the chaotic attractor. After the information about this so-called Poincaré section has been gathered, one allows the system to run and waits until it comes near a desired periodic orbit in the section. Next the system is encouraged to remain on that orbit by perturbing the appropriate parameter. One strength of this method is that it does not require a detailed model of the chaotic system but only some information about the Poincaré section. It is for this reason that the method has been so successful in controlling a wide variety of chaotic systems.

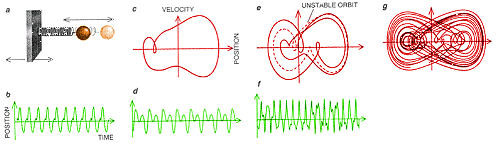
CHAOTIC ATTRACTOR consists of many periodic orbits-for example, the period-one orbit and the period-two orbit. This attractor represents a system whose velocity and position change along a single direction. One axis represents position, and the other is velocity. Attractors may be multidimensional because systems can have many different state-space variables, that is, positions and velocities that vary in three dimensions.

The practical difficulties of the OGY method involve getting the Poincaré section and then calculating the control perturbations. One of the simplest ways to obtain a Poincaré section is to measure, at some regular interval, the position of the state-space trajectory of the system. For example, the measurements could be made at the end of every cycle of the driving signal. This technique produces a map in which a period-one orbit appears as one point, a period-two orbit appears as two points and so on.

To calculate the control perturbations, one analyzes the Poincaré section to determine how the system approaches the desired orbit, or fixed point. This analysis requires three steps. First, one determines the directions along which the system converges toward or diverges away from the fixed point Second, one must obtain the rate of convergence or divergence-a quantity that is related to the Lyapunov multiplier. Last, one must figure out how much the orbit shifts in phase space if the control parameter is changed in one way or another. This three-step calculation provides the information necessary to determine the perturbations that will nudge the system toward the desired periodic orbit.

When the control parameter is actually changed, the chaotic attractor is shifted and distorted somewhat. If all goes according to plan, the new attractor encourages the system to continue on the desired trajectory. If the system starts to go astray, the control parameter is changed again, producing yet another attractor with the desired properties.

The process is similar to balancing a marble on a saddle. If the marble is initially placed in the center of the saddle, it tends to roll off one side or the other but is unlikely to fall off the front or back. To keep the marble from rolling off, one needs to move the saddle quickly from side to side. Likewise, one needs to shift the attractor to compensate for the system's tendency to fly off the desired trajectory in one direction or another. And just as the marble reacts to small movements of the saddle, the trajectory is very sensitive to changes in the attractor.

POINCARÉ SECTION is, more or less, a perpendicular slice through a chaotic attractor, in this case, a three-dimensional version of the attractor shown on the opposite page. The points of the Poincaré section represent different unstable periodic orbits. The period one orbit is a single point (red), and the period-two orbit is two points (blue). The determination of the Poincaré section is a key step in controlling chaos.

What is truly extraordinary about the work of Ott, Grebogi and Yorke is that it showed that the presence of chaos could be an advantage in controlling dynamic behavior. Because chaotic systems are extremely sensitive to initial conditions, they also react very rapidly to implemented controls. In 1990 one of us (Ditto), along with Mark L. Spano and Steven N. Rauseo of the Naval Surface Warfare Center, set out to test the ideas of Ott, Grebogi and Yorke. We did not expect things to work right away. Few theories ever survive initial contact with experiment. But the work of Ott, Grebogi and Yorke proved to be an exception. Within a couple of months we achieved control over chaos in a rather simple experimental system.

The experiment requires a metallic ribbon whose stiffness can be changed by applying a magnetic field. The bottom end of the ribbon is clamped to a base; the top flops over either to the left or right When the ribbon is exposed to a field whose strength is varied periodically at a rate around one cycle per second, the ribbon buckles chaotically. A second magnetic field served as the control parameter.

Our goal was to change the chaotic motion of the ribbon to a periodic one by applying the OGY method. We first needed to obtain the Poincaré map of the system's chaotic attractor. The map was created by recording the position of the ribbon once per drive cycle, that is, the frequency with which the magnetic field was modulated. A computer stored and analyzed the map; it then calculated how the control parameter should be altered so that the system would follow a period-one orbit through state space. We found that even in the presence of noise and imprecise measurements, the ribbon could easily be controlled about an unstable period-one orbit in the chaotic region. We were genuinely surprised at how easy it was to implement and exploit the chaos.

The ribbon remained under control without a failure for three days, after which we got bored and wanted to attempt something else. We tried to make the system fail by adding external noise, altering the parameters and demonstrating the system to visitors (a sure way to make any experiment fail). In addition, we succeeded in forcing the system to follow period-one, period-two and period-four orbits, and we could switch between the behaviors at will.

As often happens in science, discoveries lead in unexpected directions. Earle R. Hunt of Ohio University took notice of our experiments and decided to attempt to control chaos in an electronic circuit. Hunt's circuit was made out of readily available components. He was able to coax the system into orbits with periods as high as 23 and at drive frequencies as high as 50,000 cycles per second. Not only did he prove that chaos could be controlled in electronic circuits, but he also showed that scientific advances can be made on a low budget.

Hunt's chaos controller-which employs a variation of the OGY method- has the advantage that it eliminates the need to obtain a Poincaré section; information for the controller can be obtained directly from measurements of the chaotic behavior. Hunt's circuit enables the manipulation of chaos in rapidly changing systems. Armed with these results, Hunt attended, in October 1991, the First Experimental Chaos Conference, having solved a problem he did not know existed.

Hunt had unknowingly overcome a technological obstacle that had stymied Rajarshi Roy and his colleagues at the Georgia Institute of Technology. Roy had been studying the effects of a "doubling crystal" on laser light. The crystal doubles the frequency of the incident light or, equivalently, halves the wavelength. The laser used by Roy generated infrared light at a wavelength of 1,064 nanometers, and the crystal converted the light to green at a wave- length of 532 nanometers. The crystal did not work perfectly, however. If the doubling crystal was oriented in certain ways, the intensity of green light would fluctuate chaotically.
Roy was eager to control the chaos in the laser system, but he knew the OGY method would not work, because it was difficult and impractical to obtain the Poincaré section for the laser system. Furthermore, Roy was skeptical that a computer system could perform calculations fast enough to implement the OGY method. Fortunately, he had learned about Hunt's work at the conference. Less than two weeks later Roy constructed a prototype controller for their laser, and to their astonishment, it worked on the first try. Within days they were controlling periods as high as 23 and at driving frequencies of 150,000 cycles per second.

Roy demonstrated that he could control chaotic fluctuations in the laser intensity and could stabilize unstable high-period oscillations. The energy of the laser could therefore be dumped into desired frequencies instead of being distributed across a broad band of frequencies. (Roy has also employed this technique to eliminate almost completely intensity fluctuations in his laser system.) Consequently, investigators can design laser systems with more flexibility and stability than ever before.

The field of laser research has also benefited from other advances in chaos control. For example, the team of Ira B. Schwartz, Ioana A. Triandaf, Carroll and Pecora at the Naval Research Laboratory developed a method known as tracking to extend the range over which the control of chaos can be maintained. Tracking compensates for parameters that change as the system ages or that slowly drift for one reason or another.

In recent months, tracking has been applied to both chaotic circuits and lasers with astounding results. For example, the laser remains stable only for a very limited power range if the parameters of the control mechanism do not adapt. By using tracking, researchers can maintain control over a much wider power range, and amazingly, they find they can increase the output power by a factor of 15.

NONCHAOTIC SYSTEMS that are out of phase can sometimes be made to operate in phase if they are driven with chaotic signals. For example, if two period-two systems are driven with the same periodic signal (a) and start out of phase, they will remain out of phase. If the same two systems are driven with a Rössler signal (b), which is mildly chaotic, they can be coaxed to operate in phase.

One problem with the OGY method is that an unacceptable amount of time may elapse as one waits for the system naturally to approach the desired orbit in the chaotic attractor. Troy Shinbrot and his colleagues at the University of Maryland and the Naval Surface Warfare Center have demonstrated a technique that rapidly moves the chaotic system from an arbitrary initial state to a desired orbit in the attractor. When Shinbrot and his co-workers implemented their method in the magnetic-ribbon experiment, they were able to reduce the time needed to acquire unstable orbits by factors as high as 25.

Another collaboration that emerged from the First Experimental Chaos Conference led to the first technique for controlling chaos in a biological system. The team-which included Ditto, Spano, Alan Garfinkel and James N. Weiss of the School of Medicine, University of California at Los Angeles-studied an isolated part of a rabbit heart. We were able to induce fast, irregular contractions of the heart muscle by injecting a drug called ouabain into the coronary arteries. Once this arrhythmia started, we stimulated the heart with electric signals that were generated according to a scheme we adapted from the OGY method. These seemingly random signals were sufficient to establish a regular beat and sometimes reduced the heart rate to normal levels. On the other hand, signals that were random or periodic did not stop the arrhythmia and often made it worse.

Investigators have already begun to test whether variations of the OGY method could be used to control arrhythmias in human hearts. They suspect the technique might work for atrial or ventricular fibrillation, in which upper or lower chambers of the heart contract irregularly and cease to pump blood effectively. In the near future, it may be possible to develop pacemakers and defibrillators that take advantage of techniques for controlling chaos.

Scientists and engineers have just begun to appreciate the advantages of designing devices to exploit, rather than avoid, nonlinearity and chaos.Whereas linear systems tend to do only one thing well, nonlinear devices may be capable of handling several tasks. Nonlinear applications promise more flexibility, faster response and unusual behaviors. As we continue to investigate the nonlinearity inherent in natural and physical systems, we may learn not just to live with chaos, not just to understand it, but to master it.