 |
Shadows from Higher Dimensions
|
Ivars Peterson
THE CLASSIFICATION GAME
Like botanists, mathematicians suffer from the urge to classify. Unlike
botanists, who can never be sure that every plant species on earth has been
collected and categorized, mathematicians can sometimes prove that a
classification scheme for a given set of mathematical objects is complete.
They can formulate an ironclad guarantee essentially stating that no one
will ever discover an object that belongs to the set yet doesn't fit one
of the mandated categories. What keeps the game interesting, however,
is that such proofs are often elusive. To mathematicians, success or failure
in these classification efforts serves as a test of the power of their
mathematical methods.
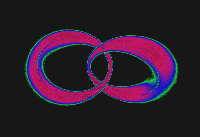 |
| FIGURE 4.10 Two linked toroidal energy-momentum surfaces for a pair of linear harmonic oscillators. |
One of the greatest classification quests in mathematics, which still isn't
over, is the search for a complete classification of geometric shapes. The
task was relatively easy centuries ago, in the days when the family of known
geometric forms encompassed familiar, well-defined, rigid figures: lines
and circles, triangles and cubes, assorted polygons and polyhedra. Then topology
reared its rubbery head, and flexibility became the rule. On top of that,
the spread of geometry into higher dimensions, from curves and surfaces into
manifolds, left mathematicians with an unruly zoo of geometric forms. Attempts
to classify these myriad shapes tended to lag behind discoveries of new ones.
It was as if a botanist, not yet finished with the earth, were faced with
a rapid succession of new worlds of exotic species, all defying easy
classification.
One of the major triumphs of nineteenth-century mathematics, and of topology
in particular, was the complete classification of two- dimensional surfaces
(two-manifolds). As outlined in the previous chapter, all surfaces, if they
are treated like plasticene sheets, can be bent, stretched, curved, or deformed
- so long as they are not torn or glued-until they match a set of basic forms.
Every conceivable surface, from the skin of a doughnut to the convoluted
exterior of a piece of coral, is equivalent to a sphere with a certain number
of attached handles and a certain number of "ends," or punctures, that penetrate
its skin. Because the number of handles (or genus) of a surface never changes
no matter how the surface is deformed, this quantity stands as a way to classify
surfaces. Hence, the surface of a coffee cup and the skin of a doughnut,
having the same genus, fit in the same category: a one-handled, or one-holed,
sphere.
Three-manifolds aren't quite so simple to classify. They're more difficult
to visualize, and four-space allows plenty of room for their strange, complex
forms. A human being in three-space would have the same trouble that a
nearsighted ant crawling on the surface of a rather large doughnut would
have in telling whether the doughnut has a hole. The ant can't stand outside
the surface and see the hole, and it can't step off the surface to fall into
it. The hole can be seen clearly only from a higher dimension. Similarly,
a human explorer wandering around on a three-manifold wouldn't see much out
of the ordinary. It needs a vantage point in four-space to detect holes and
other features of a three-manifold.
However, we can try some indirect approaches to the hole-detection problem.
An inquisitive ant, wondering whether its surface is a sphere, torus, or
some other exotic form, could detect a hole by taking circular tours around
the surface. The ant carefully notes the properties of these closed loops
as they shrink in size. Sometimes, the ant's path will form a closed loop
that happens to thread its way through a hole. In that case, the ant would
find that its circular path can't be shrunk beyond a certain point; it gets
snagged on the hole. Loops that don't thread a hole, however, can be shrunk.
If an ant finds that all possible closed loops on the surface can be shrunk,
then it knows it's on a sphere.
The ant's experiment can be turned into a useful mathematical procedure for detecting holes. This procedure forms the basis for an algebraic method, developed by Henri Poincaré at the turn of the century, to detect and study the pattern of holes in a topological surface. His strategy, like the ant's, depends on the shrinking properties of loops on a given surface.
All closed paths on a sphere can be continuously shrunk to a single point.
That sphere, then, is said to be simply connected. In contrast, there are
fundamentally different types of paths on a torus, only some of which can
be shrunk to a point (see Figure 4.11). Those winding through the center
hole differ from those winding around the center hole. And both are different
from the cyclic paths that loop through the center as they go around the
torus. Every surface other than a sphere contains some unshrinkable loops.
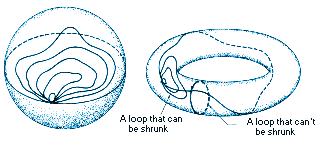 |
| FIGURE 4.11 Loops on a sphere and a torus: some loops can be shrunk to a point: others can't. |
Poincaré expressed his scheme in terms of an algebraic structure called
a group. In this context, a group is a kind of exclusive club whose
members obey a set of strict mathematical rules. It's also a way of expressing
compactly certain characteristics of mathematical objects; in this case,
the shrinking properties of loops on surfaces. Poincaré's fundamental
groups specify the way in which closed loops on a manifold may be deformed
into one another.
For a two-sphere, the fundamental group consists of a single member because
any loop lying on a sphere may be tightened like a noose until it is shrunk
to a point. For this and other reasons, topologists consider the two-sphere
to be the simplest of all surfaces - the one with the fewest topological
complications. A torus requires two winding numbers, which represent
the number of times a curve winds around the body of the torus (like the
stripes on a candy cane) and the number of times a curve winds around the
hole in the middle. Hence, the fundamental group for a torus consists of
a pair of generators for representing the two possible winding numbers.
This means that the two-sphere and the torus are associated with different
groups, reflecting the fact that the two surfaces are topologically distinct.
One can't be deformed into the other. In this way, all possible two-manifolds
can be labeled, and every surface fits into a particular category given by
its fundamental group. That labeling matches the classification scheme based
on the number of handles, or holes, a surface has. For a complicated shape,
calculating the Poincaré group provides a handy way of classifying
the object.
One consequence of this scheme is that for two-manifolds, any surface that
happens to have a one-member, or trivial (as mathematicians like to call
it), fundamental group must be topologically equivalent to a two-sphere.
A three-dimensional sphere also turns out to have a trivial fundamental group.
considering the family resemblance between two- spheres and three-spheres,
Poincaré conjectured that three-dimensional spheres behave just like
two-dimensional ones. Any three-manifold that is associated with a trivial
fundamental group should be deformable into a three-sphere. That is, any
three-manifold that behaves like a three-sphere is a three-sphere. There
are no fake spheres.
The Poincaré conjecture, still unproved despite numerous heroic efforts
over the last few decades, ranks as one of the most challenging and baffling
unsolved problems in mathematics. Whole fields of mathematics have been developed
in the course of testing, on a case- by-case basis, not only the conjecture
itself but also the extension of the conjecture to manifolds in higher
dimensions.
The central problem in proving the Poincaré conjecture is that, unlike
the two-manifold case, no one knows a classification scheme for three-manifolds.
There is no list of all possible surfaces that can be checked one by one
to make sure that all nonspheres contain unshrinkable loops. Even worse,
attempts to classify three-manifolds seem to depend on knowing that the
Poincaré conjecture is true. The only way out is to develop totally
new methods that bypass the unsolved classification problem.
Ironically, the first major advances toward proving the Poincaré
conjecture occurred not for three-manifolds but for higher-dimensional manifolds.
One important tool for the study of higher-dimensional manifolds, developed
in the early 1960s, was the technique of surgery: systematically studying
the effect of removing certain pieces of a manifold, then gluing them back
with a specific twist (see Figure 4.12). In 1961, Stephen Smale developed
and used just such a surgical method to break manifolds into digestible,
bite-size pieces that could be easily moved around. His work led to a
far-reaching theorem, one of whose consequences was the truth of the
Poincaré ' conjecture for five- and higher-dimensional manifolds.
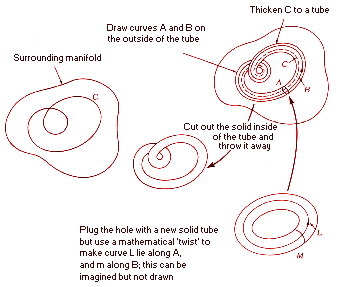 |
| FIGURE 4.12 An example of topological surgery: removing a tube and then gluing a new one back in with a "twist." |
These higher-dimensional manifolds turn out to be easier to classify than
three- or four-manifolds, but even spheres, the lowliest of higher-dimensional
manifolds, sometimes display unexpectedly bizarre properties. For example,
John Milnor in 1959, doing a kind of multidimensional plumbing- cutting holes
here and there, connecting them by various tubes, then deforming the result
into a new kind of sphere-stunned the mathematical world by showing that
the seven-dimensional sphere can be made into a smooth, or "differentiable,"
manifold in 28 different ways. Milnor's result means that Poincaré's
scheme of representing the solutions to differential equations on manifolds
would, in dimension seven, encounter 28 different versions of the sphere.
After a spurt in the 1960s, efforts aimed at proving Poincaré's conjecture
stalled. Two cases remained: three-manifolds and four- manifolds. That left
mathematicians with the feeling that something unusual happens in spaces
of dimensions four and five. In both, the number of dimensions is high enough
to allow complicated behavior, but too small to leave sufficient room for
mathematical maneuvering to eliminate those complications.
Four-manifolds finally fell into place in 1982. Using a system of flexible
handles, Michael Freedman of the University of California at San Diego
blended loops, surgery, and boundaries to solve several major problems in
four-dimensional topology and to give a complete classification of all simply
connected, or spherelike, four-dimensional manifolds. His basic idea was
to start with a four-dimensional disk and build up a given four-manifold
by adding handles one by one. One consequence was a proof of the Poincaré
conjecture for four-manifolds. In addition, Freedman's extraordinary work
unearthed several previously unknown examples of four-manifolds and many
unsuspected connections between known manifolds.
In proving the conjecture, Freedman also took a big step toward classifying
all four-manifolds. These manifolds fall into two types. Differentiable
manfiolds change smoothly, one feature blending into the next.
Topological manifolds, a broader category that encompasses differentiable
manifolds, also include surfaces that sometimes resemble earthquake-torn
globes, having tortuous, jagged landscapes that change abruptly from place
to place. Freedman proved that although every differentiable manifold is
also a topological manifold, not all topological manifolds are differentiable.
This phenomenon first occurs in four dimensions.
Furthermore, Freedman constructed a particular topological four-dimensional
manifold called E8, which has eight two-dimensional holes and is so convoluted
that it can't be smoothed. Freedman's proof that such a manifold exists led
to the astonishing discovery, by Oxford mathematician Simon Donaldson, of
a new four-dimensional space. Donaldson's result sharpened the view of many
mathematicians that four-dimensional geometry is truly more interesting and
complicated than initially they had any right to think.
What makes Donaldson's surprising discovery particularly intriguing is that
it concerns four-dimensional space - a space that is clearly of physical
importance and a space that is not particularly abstract. Physicists now
suddenly face the mind-boggling prospect of having more than one mathematical
way to construct what they conceive of as ordinary four-dimensional space-time.
The geometric rules governing the two four-spaces are the same, but their
structures are different.
Perhaps this new four-dimensional structure has no physical meaning, or
perhaps it means that the universe we inhabit has a more peculiar structure
than anyone ever imagined. In fact, the universe could be as convoluted as
a tangled loop of string. Or there may be space-time universes, organized
in different ways but coexisting with ours, with which we can't communicate
in any way. Donaldson's startling mathematical result has provided physicists
with much food for thought.
Freedman's work left just the original Poincaré conjecture unsolved - the case for three-minifolds. Mathematical surgery suggests why the three- manifold case is so complex. Surgery makes it possible to construct a three-manifold from any tangled loop of string, no matter how knotted or convoluted the tangle. As in knot theory, that's like confronting two separately snarled masses of fishing line and trying to determine whether or not the two piles of line are tangled in the same way. Unless it's possible to classify such tangles of line in a systematic way, there seems to be no hope that three- manifolds can be analyzed either. Solving one problem would solve the other.
Yet even the three-manifold case may be within reach. In 1982, Princeton
University's William P. Thurston
set forth a program that could lead to the
classification of three-dimensional manifolds and a resolution of the original
Poincaré conjecture. Thurston's approach uses surgery to reduce complex
manifolds to simple cases in much the same way that factoring reduces large
composite numbers to products of primes.
Thurston found a geometric pattern that may turn out to encompass all possible
three-manifolds. The pattern involves a surprising connection between
three-manifolds and the curved spaces of noneuclidean geometry. A century
ago, topologists believed that only two- manifolds can be described as being
flat (having zero curvature), spherical (positively curved), or saddle-shaped
(hyperbolic or negatively curved). Three-manifolds look too complicate to
fit into such simple categories. Unlike a two-manifold, which can be specified
and listed according to its genus, every three-manifold, like a tangled loop
of string, seems to have its own distinctive properties and to resist fitting
into any larger pattern.
The example of two-manifolds suggests possible ways to tame the unruly
three-manifolds. Two-manifolds can be represented as many- sided, or polygonal,
figures whose edges are glued together in a particular way. For instance,
a Flatlander moving on a square may find that when he moves off the top edge
of the square, he reappears at the bottom. When the creature moves off the
right edge, it reappears at the left. Many video games operate on the same
principle to keep a figure on the screen. Such movements can occur if, in
some sense, the top of the square is glued to the bottom, and the right edge
to the left. What does the resulting surface look like? The first gluing
creates a cylinder; the second curves the cylinder into a doughnut. The doughnut
and the square topologically count as the same abstract manifold: a two-torus
(see Figure 4.13).
This gluing trick turns out to be useful in bringing geometry back into the
study of three-manifolds, making many manifolds more easy to visualize. A
three-manifold, for example, can be generated from a rectangular block, such
as the space inside a room. It's a matter of abstractly gluing the front
wall to the back wall, the left wall to the right wall, and the floor to
the ceiling. If we actually made these gluings, the result would be a room
that has to bend around and join itself in the fourth dimension. But all
that is needed for the description of the manifold is given by the procedure
for abstract gluing. A human being living in such a house would probably
find its geometry quite disconcerting-walking through one wall and ending
up on the opposite side of the room, going through the ceiling to come up
through the floor, disappearing at one wall and reappearing at another. Because
such motion is strikingly similar to a Flatlander's motion on a two-torus,
this particular three-manifold is called a three-torus. Abstract gluing shows
the close tie between curved three-manifolds and polyhedra such as the
rectangular block.
However, at least two major differences hold between the geometry of two-manifolds and the geometry of three-manifolds. First, whereas two-manifolds can have three types of local geometry (flat, spherical, and hyperbolic), three-manifolds can be given five additional types of local geometric structure. The additional geometries are conceivable because in three or more dimensions a curvature is defined for each two-dimensional slice that passes through a point. Second, it is possible to combine three-manifolds in such a way as to yield new three-manifolds that cannot be given a locally homogeneous geometry. Fortunately, topologists know how to split a three- manifold into primitive pieces by purely topological methods.
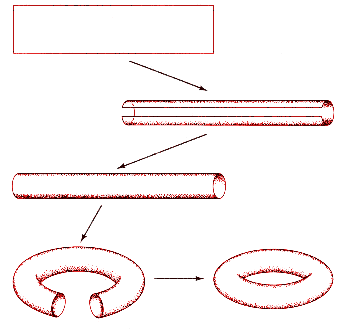 |
| FIGURE 4.13 A torus is topologically equivalent to a rectangle: gluing the opposite edges of a rectangle turns it into a cylinder; joining the free pair of edges turns the cylinder into a torus. |
In 1980, Thurston proved that most three-dimensional shapes fit into the
hyperbolic category and that many exceptions fit into one of seven other,
rarer classes of geometric forms. He conjectured that by looking at small
pieces or neighborhoods within a manifold, topologists can put each piece
of the manifold into one of eight categories, based on the geometric shape
of the neighborhood. It's like having eight basic sets of clothing that fit
anybody in the world. In a sense, mathematicians impose a geometric structure
on a manifold by cutting it into a polyhedron that can then be abstractly
glued back together in one of the eight basic geometric types. The trick
is to prove that the eight geometric categories suit all conceivable
three-manifolds.
Thurston's conjecture has been proved for wide classes of three- manifolds,
and it has been tested by experiment on many other examples, either by hand
or with the aid of a computer. So far, Thurston's scheme has never failed,
and many mathematicians think it's unlikely a counterexample will be found.
But no one knows yet for sure.
Thurston's insight has also brought some rigidity back into topology. Normally,
topologists study properties that don't change when a shape is deformed.
Thurston showed that sometimes it helps to impose a rigid geometric form
to pin down topological structures. It makes classification, at least for
three-manifolds, easier.
The lack of a proof for the Poincaré conjecture hasn't stopped
mathematicians, however. They work around the conjecture by scrupulously
avoiding hypotheses that depend on the truth of the Poincaré conjecture.
Such caution is typical of mathematicians. Although most believe that the
conjecture is true, a definitive proof is necessary before it can become
part of the structure of mathematics. Moreover, as a result of this caution,
when a proof finally comes, it won't directly affect much of the work topologists
have already done. But the proof itself will likely involve new mathematical
methods that turn out to be useful elsewhere.
