 |
Shadows from Higher Dimensions
|
Ivars Peterson
LINEAR GYMNASTICS
The Too-Good-To-Be-True Bakery is famous for its best-selling bran muffins
and carrot cakes. The shop sells a dozen muffins at a profit of $2.50 and
a carrot cake at a profit of $1.50. With high demand and an unlimited supply
of ingredients, the baker's choice is clear. Baking more muffins means earning
a greater profit. One day, the baker notices that she has only a limited
amount of flour on hand. Eggs are scarce. Her supply of honey is about to
dry up. Because the recipes for bran muffins and carrot cake call for different
proportions of these ingredients, the path to maximum profit is no longer
quite so clear- cut. A dozen bran muffins require more flour than a carrot
cake. Baking only muffins would use up all the flour and may let too much
of the other ingredients go to waste. Perhaps baking a combination of both
muffins and cakes would use up more of the ingredients and net a higher return.
The baker's plight is a simple, hypothetical example of a type of mathematical
problem that involves finding the best solution among many possible answers.
The mathematical techniques invented to solve such problems allow managers
and planners to establish optimal strategies for allocating time, money,
or supplies to keep costs down, profits up, or projects on schedule. To use
these techniques, planners must be able to express the main features of their
real-world problems in mathematical terms, without overlooking essential
details and without excessively distorting reality.
Linear programming (where "programming" means planning) was invented
to make such choices easier. "Linear" refers to the type of equations used
to express the constraints bracketing a given situation. In making muffins,
for example, the amount of each ingredient needed is assumed to be proportional
to the number of muffins produced. Doubling the number of muffins doubles
the amount of flour consumed; it also doubles the profit from the sale of
muffins.
In the bakery problem, suppose that it takes 2 cups of flour to make a dozen
muffins and only 1 cup to make a carrot cake. The total amount of flour
available, 50 cups, limits the number of muffins and cakes that can be produced.
That constraint can be expressed as an equation in terms of two variables.
If B represents the dozens of bran muffins to be produced and C the number
of carrot cakes, the constraint equation is simply 2B + C = 50. It says that,
considering only flour supplies, the baker can choose to make 25 dozen muffins
and no carrot cakes, or 50 carrot cakes and no muffins, or any one of innumerable
other possibilities, just so long as the total amount of flour consumed is
never more than 50 cups. Similar equations express other constraints, such
as the limited supplies of honey and eggs.
With just two variables, all the equations can be drawn as straight lines
on a two-dimensional graph (see Figure 4.14). Each line divides the plane
into two regions. One half encompasses the area where every point (B, C)
represents a possible answer; the other half is a forbidden zone. The complete
collection of straight-line constraints fences in an area the shape of an
irregular polygon within which the optimal answer must be found.
Which is the best of all possible answers? One way to find out is to compute
for each pair of allowed values what the profit would be and then select
the pair that gives the largest profit. But mathematics provides a convenient
shortcut through this tedious procedure. In general, the optimal answer lies
at one particular corner, or vertex, of the polygon. The coordinates of that
vertex (B, C) provide values of B and C for which the total profit will be
highest.
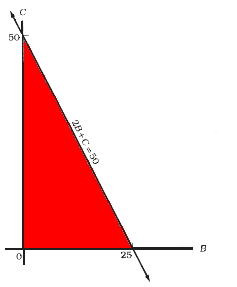 |
| FIGURE 4.14 solving the bakery problem. Because B and C can't be negative, possible answers lie within the shaded area. Other constraints further restrict the area in which feasible values lie. |
Real-world business problems - from routing telephone calls to scheduling
airline flights and allocating tasks to a work force - may involve hundreds
or even thousands of variables and constraints. For these problems, the
constraint equations form a complicated nest of hyperplanes in a high-dimensional
space. As in the simpler two-variable case, each hyperplane cuts this enormous
space in half. On one side of the surtace are points corresponding to feasible
plans of action; on the other side lie infeasible points, which violate the
constraint represented by the surface. Together, the intersecting hyperplanes
create a multidimensional polyhedron called a polytope, which encloses all
the feasible solutions. In this case, too, the best answer lies at a vertex.
Solving a linear programming problem is something like climbing to the top
of an elaborate, irregular geodesic dome. Step by step, the appropriate
mathematical algorithm steers the climber through a space that may be thousands
of dimensions in extent to the peak of the polytope. What's needed is an
efficient way to close in on the right corner.
The simplex method, introduced in 1947 by George B. Dantzig of Stanford
University, navigates toward the answer by mathematically hopping from one
vertex to an adjacent vertex across the polytope's surface, always taking
the branch that leads "uphill," toward the "peak" vertex, which represents
the optimum values for the given set of variables (see Figure 4.15). Using
the simplex method effectively is virtually an art. Theoretically, because
the number of vertices to be visited may be immense, a computer could take
practically forever to reach the right corner. In practice, the simplex method
is surprisingly efficient, and years of work have refined it considerably.
While just about any programmer can state the method's essence in a computer
program of about two dozen lines, actual programs run to more than 50,000
lines. These elaborate steering mechanisms are replete with clever programming
ploys that drive the algorithm to Its goal more quickly. Only rarely, In
a few pathological cases, is the method slowed down significantly because
practically every vertex has to be visited before the peak vertex is at last
attained.
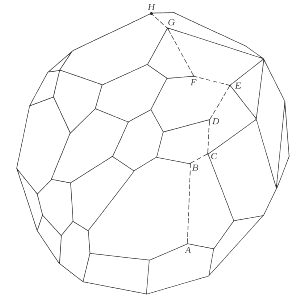 |
| FIGURE 4.15 Starting at A. the simplex method proceeds from vertex to vertex until it reaches an optimal value at H. |
Over the years, the simplex method has gradually been improved and has now
reached the stage where one or another of its many variants can process problems
with 15,000 to 20,000 constraints. Beyond this, the simplex algorithm generally
becomes prohibitively slow and cumbersome. Unfortunately, many of today's
business problems - especially those in the telecommunications industry -
have far more than 20,000 constraints and variables.
In 1979, Russian mathematician L. G. Khachian introduced a method that seemed
to overcome some of the simplex method's limitations. Khachian's method requires
the construction of high-dimensional ellipsoids (in two dimensions, they
would be ellipses) around the entire structure. These enveloping,
high-dimensional balloons "slide" sideways under the influence of the polytope's
constraining surfaces, so that the centers gradually close in on the optimal
solution. This procedure guarantees that a computer will complete its job
within what computer scientists call polynomial time, whereas the simplex
method, at its worst, runs in exponential time. The same kind of time constraints
are important for evaluating methods for factoring numbers.
The difference between polynomial time and exponential time is like the
difference between x3 and 3x Say x
is 10; then x3 is 1,000 and 3x is
59,049. As the value of x (for example, the number of variables in
a linear programming problem) increases, exponential time quickly becomes
astronomical. On worst-case problems for the simplex technique, when the
problem size is doubled, the time required to process such a problem is squared.
For the ellipsoid method, when the problem size doubles, the processing time
for a worst-case problem goes up by a smaller factor.
However, the Russian algorithm proved disappointing: in practice, it turns
out to be far slower than the simplex method for most everyday problems and
has an advantage only with very large numbers of variables. Except in certain
pathological cases, the simplex method completes the job in about as many
steps as there are variables. The worst case, in which every vertex must
be visited, rarely comes up. The ellipsoid method, however, shows no such
convenient behavior.
In the last few years, a new, remarkably efficient method, discovered by
Narendra K. Karmarkar of AT&T Bell Laboratories, has taken the spotlight.
Karmarkar's algorithm boldly jumps away from the concept of a surface path
zigzagging from vertex to vertex on a polytope of fixed shape. Instead,
Karmarkar's algorithm plunges into the polytope's interior and works from
the inside, guided by step-by-step transformations of the polytope's shape.
Karmarkar's search for the peak starts with a point that lies within the
polytope. The first iteration twists the polytope, according to the rules
of projective geometry, into a new shape centered around the starting point.
From this newly established, central vantage point, the algorithm takes a
step, following the path of steepest ascent or descent, to the next approximate
solution point within the poly tope's interior. That's done by inscribing
a sphere within the polytope (like blowing up a balloon inside a box until
it just fits without being scrunched) and selecting a new point near the
sphere's surface in the direction of the best solution. Then the polytope
is warped again to bring the new point to the center. Successive applications
of these projective transformations have the effect of magnifying the parts
of the feasible region close to the optimal vertex. In only a few steps,
Karmarkar's method converges on the optimal solution.
Bounds, called performance guarantees, strictly limit how long an
algorithm takes to do its job in the worst possible case and are important
in theoretical computer science. Like the ellipsoid method, Narendra Karmarkar's
scheme also runs in polynomial time, but the exponent governing how long
his method takes is smaller than the exponent governing the ellipsoid method.
The bound on Khachian's algorithm grows as n6, rendering
it impractical for large problems involving thousands of variables. Karmarkar's
method grows as n3.5, a significant improvement over the
previous polynomial-time algorithm. As a result, when the number of variables
in a problem increases, the running time for Karmarkar's method doesn't rise
as rapidly as it does for the ellipsoid method. Moreover, the new method,
when cleverly implemented in a computer program, in many cases seems to perform
significantly faster than the simplex algorithm.
Speed does make a difference. The old joke that it takes 3 days of calculations
to predict tomorrow's weather pinpoints the crucial problem. Using known
methods and algorithms, many complex problems take too long to solve. Although
the simplex method was, for a long time, the best technique known for solving
linear programming problems, it had its limits. Karmarkar's method pushes
up the number of variables and constraints that can be handled within a
reasonable time. Such a vast increase in the number of variables that can
be handled in a linear programming problem may reshape many theories in economics
and perhaps other sciences. Problems that people once avoided because there
was no method for solving them may be now within reach.
