
 |
How it works : Relativity |
RELATIVITY
The theory of relativity is divided into special and general relativity, and involves corrections to some of the laws of 'classical' or Newtonian physics where very high velocities are concerned; a relationship between mass and energy; and a theory of gravitation. Historically, the Special Theory of relativity came first, in 1905, followed in 1916 by the General Theory.
 |
Henri Poincaré (1854 - 1912) the true originator of
theory of relativity. He coined the term in 1904, and had already
pointed out the consequence that nothing can travel faster than light.
|
The Special Theory was developed independently by Henri Poincaré in Paris and Albert EINSTEIN in Zürich. During the few years before 1905 it was becoming clear that the old ETHER theory of electric and magnetic fields was becoming inadequate. The Michelson-Morley experiment had failed to detect the Earth's motion relative to the supposed ether, which was thought to be the medium which transmitted the vibrations of light and radio waves. If this was so, then the difference in the speed of light caused by the Earth's motion through the ether ought to have been detectable. The Michelson-Morley experiment's very failure provided a startling piece of evidence: it showed that the speed of light is the same, even if the source of the light is moving towards or away from the observer at a large fraction of that velocity. This observation led to the even more surprising predictions of relativity.
Hendrik Lorentz in Amsterdam was able to show that the motion through the ether could not be detected, and Poincaré claimed that indeed it could never be detected. He introduced the principle of relativity: 'the laws of physical phenomena must be the same for a fixed observer as for an observer who has a uniform motion of translation relative to him so that we have not and cannot possibly have any means of discovering whether we are being carried along in such a motion.' During the next year Poincaré developed this new physics, while at the same time Albert Einstein, then an unknown clerk in the Swiss Patent Office, was pursuing a critical analysis of the measurement of space and time that led to the same results, the theory we now call special relativity. Today the analysis of Einstein is the one normally given in the text books and is the one to be followed here.
Synchronizing clocks
Einstein began by asking how we can say that two events took place at
the same time. This is important because it takes time for light to travel
from an event to us so that the time when we see something happening is later
than when it actually happened. Of course, for nearby events this correction
is normally insignificant but for very distant events it is crucial.
One way of transferring our local measurement of time is simply to use our own clock and to send out light signals to be reflected back to us from any distant object; this is known as the radar method. Alternatively, we could arrange for a network of clocks to be arranged throughout space, each clock synchronized to agree with our own, and note the time on the clock situated at the same place as the event whose time is to be recorded. But in order to follow this method, we have to synchronize the clocks to make sure they agree with our clock, and again we have to use light signals to set these clocks.
This is done by sending out a signal which is reflected back by the distant clock and returns to the original clock. The distant clock is then synchronized with our clock if the time on the distant clock when it received the signal is half way between the time of emission and the time of reception on our clock. If a signal was emitted at 01.00 on our clock and returned at 03.00 on our clock then the distant clock is synchronized if it read 02.00 when it received the signal. In making this rule, or Einstein convention as it is called, for setting clocks we are requiring the velocity of light to be a constant, the same in both outward and return journeys. Besides setting clocks by this radar method it is also possible to measure distance in terms of time and the value of the velocity of light, 186,000 miles per second (300,000 km/s) which is normally written as c. This is done by:
distance = (time of reception - time of
emission)´ c
2
and is expressed in light seconds, or light hours, but can easily be turned into other units. In the example we have just used, the distance is one light hour or 669,600,000 miles (1,130 million km-in the solar system, this is equal to the distance between the Earth and a point between Jupiter and Saturn).
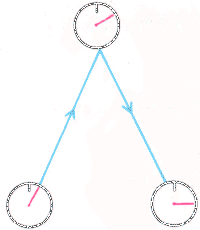 |
Light takes an hour to travel from one clock to the other. The distance is measured by multiplying half the round trip travel time by the velocity of light |
Combining these rules for distance and time measurement with the principle of relativity, that the laws of physics should be the same for all uniformly moving observers, Einstein was then able to show that clocks synchronized for one observer were not synchronized for another moving past him with a uniform velocity; that is, synchronization is relative, not absolute. Time as measured by a moving observer must go at a different rate to that measured by a stationary observer.
To see this, imagine that an observer O has his own clock and at the moment he passes an observer A he sets it to zero to agree with A's clock. From A a light signal is sent out when A's clock reads 1 second. Suppose this reaches O when his clock reads 2, and it is then reflected back to A, then back to O . This situation is best understood with the help of a space-time diagram, showing the change of distance with time:
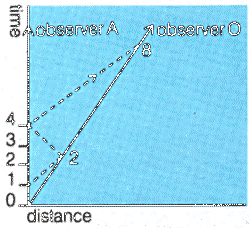 |
A graph of time against distance travelled. An object travelling at an unvarying speed is represented by a straight sloping line: its slope indicates the speed |
The principle of relativity can now be used to find the time of arrival of the signal back at A. The time between O and A being together and A sending out the signal was one second, and the time between O and A being together and O receiving the signal is twice this or two seconds. But any relationship between O and A is equally true the other way round: a signal sent from O one second after A and O were together reaches A at twice this or two seconds. The signal that leaves O at two seconds on O 's clock reaches A at twice this or four seconds on A's clock. By the Einstein rule A says that the signal reached O halfway between emission and reception or at a time of two and a half seconds. This is the time that would be on a clock at the reflection that was synchronized with A. But O's clock reads 2 at this reflection, so O and A associate a different time to the reflection by O.O's time is four-fifths of A's time. Using the same signals we can calculate the velocity of O relative to A. Since A finds the round trip travel time to be three seconds the signal travelled a distance of 1½ light seconds or 1½c from A to O and it got there at a time of 2½ seconds. O therefore travelled 1½c in 2½ seconds so his velocity is
| velocity | = | distance | = | 1½c | = | 3c |
| time | 2½ | 5 |
that is, 3/5 the velocity of light.
At first sight it seems strange that O's time is slower than
A's, since by the principle of relativity what is true between
A and O is equally true between O and A. This
is indeed so, for if the light signal reaching A at four seconds is
reflected back to O it reaches him at time 8 on O's clock (again
the factor of two), so O calculates the time of arrival of the signal
at A by taking it halfway between emission at two seconds on
O's clock, and reception at eight seconds on O's clock, namely
five seconds, but A's clock reads four seconds or 4/5 of O's
time just as it was the other way round. For both experimenters, the moving
experimenter's clock goes slow compared to the time assigned by himself.
It has often been claimed that this is a paradox, for how can O be
slower compared to A, and A slow compared to O ? There
is no paradox since we are not comparing O and A's clocks,
but rather O 's clock with A's assigned time or synchronized
clocks in the first case, and A's clock with O's assigned time
or synchronized clocks in the second. The relativity principle requires that
the relationship between A and O be symmetrical and it is.
While we have just calculated a particular example for a velocity of
3/5c it is possible to work out the results for any velocity v.
Signals emitted one second apart are then received by the other observer
at intervals given by
| 1+v/c | secs | |
| 1-v/c |
For v/c = 3/5 this is just the factor of two that we found. The time assigned by the stationary clock and the time measured by the moving clock are found to be related by the expression
| time measured on moving clock = | 1 |
| time assigned by stationary clock | Ö1-v2/c2 |
Evidence
There is now a wealth of experimental data that supports the slowing
down of moving clocks, or time dilation as it is called. The simplest
comes from particles called mu mesons, which are produced about six
miles (to km) up in the Earth's atmosphere where particles from outer space
known as cosmic rays hit the atoms of the atmosphere. These mu mesons are
well known from laboratory experiments and they are unstable, only living
about two millionths of a second before they split up into other particles.
Even travelling at the speed of light they could only travel about one third
of a mile before decaying, yet we see them at the Earth's surface. But as
they do travel with velocities close to the velocity of light, their aging
is slowed down. If their speed were 3/5c they would live for 20% longer,
but if they were moving at 99.9% of the speed of light they would live for
over twenty times longer, enough for them to penetrate down to the Earth's
surface.
 |
Mu mesons can reach the Earth's surface despite their short lives because their high speed makes time run slower for them |
Lorentz transforms
The fundamental result of special relativity is known as
the Lorentz
transformation, which relates the measurements of distance as well
as time by two observers moving with any speed v. We can understand
this by a similar calculation to the one that gave the time dilation, where
we have two observers A and O moving relative to each other
with velocity v, and having set their clocks to zero when they passed
each other. A now sends out a signal to be reflected back to him from
an event E. On its route the signal passes O, is reflected
by E, passes O on the way hack and finally reaches A
again. A calculates the distance and time, say l and t of
E by the standard radar convention using his clock readings. O
does a similar calculation using his clock and obtains values L and T,
but since the rate of O 's clock is known if the velocity is known,
L and T can be expressed in terms of l and t. If
this is done we find that
| L= | l - vt | T= | t-vl/c2 |
| Ö1-v2/c2 | Ö1-v2/c2 |
These are the Lorentz transformations, which were first developed by Poincaré who corrected an error in earlier calculations by Lorentz.
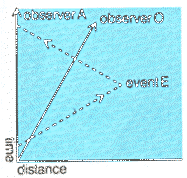 |
Observer O travels at a fraction of the speed of light (the slope of the dotted line). When A and O compare their timings of the light travelling to E and its reflection, they will differ. The relationship between the measurements is called the Lorentz transformation |
Another important result is the addition of velocities. Both Poincaré and Einstein realized that the addition law of velocities had to be changed so that the result of adding velocities below the velocity of light always gave a velocity less than that of light. For imagine that besides observer A there is observer O moving with 3/5c in one direction and observer Q moving with 3/5c in the opposite direction. If simple addition were correct Q would be moving with a velocity 6/5c relative to O but this cannot be the case since a light signal travelling at speed c can pass from O to A, and the same signal can pass from A to Q, so O can communicate with Q. He could not do this if their separation velocity were 6/5c as the light signal would not reach him. The velocity of O relative to Q is calculated by considering a signal that leaves O at time 1 on O's clock, reaches A at time 2, goes on to Q getting there at time 4 on Q's clock, getting back to A at 8 and on to O at time 16 on O's clock. O now calculates the distance and time of the reflection at Q as
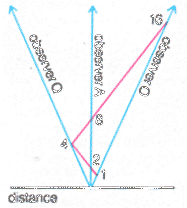 |
The times shown are those on O's clock, but his only way of knowing the time of the reflection at Q is to take the average of the starting and final times. Although the observers are separating at more than the speed of light, light signals can still travel between them |
| distance = | 16-1 | c | = | 15 | c, | time= | 16+1 | = | 17 | ||
2 |
2 |
2 |
2 |
The velocity of Q relative to O is therefore given by dividing the distance by the time, giving 15/17c.
In general if A has a velocity v relative to O , and Q has a velocity V relative to A, the velocity of Q relative to O is
| U = | V + v |
| 1 + vV/c2 |
a result first discovered by Poincaré and independently by Einstein.
 |
| The penetration, and hence momentum, of the shell is the same for both observers. But to the rocket observer the shell has moved slower, since his clocks run slower. He concludes that the shell is more massive as a result of its velocity relative to him |
Since velocities do not simply add together as in the pre relativistic Newtonian physics, some correction to this theory is necessary; because the continued application of a force cannot accelerate a body to beyond the speed of light. In Newton's theory the momentum of a body (its mass multiplied by its velocity) is what changes when a force acts, and if the velocity is not to increase beyond c, then the mass must vary with velocity becoming larger and larger as the speed approaches that of light. A simple way of seeing this is to consider a shell being fired into armour plating and measuring how far it penetrates. This penetration is the same for an observer standing with the gun as for another observer moving with a large velocity perpendicular to the line of fire. The moving observer does not measure the same velocity for the shell, however. His clocks are slowed down so he measures a velocity lower by the factor Ö1 - v2/c2. But the penetration depends on the momentum or mass ´ velocity and is the same, so the mass must be larger by the same factor, and so increase with increasing velocity.
It also follows from the correction to Newtonian physics that mass and energy ate not separate quantities but are essentially the same thing. This relation is usually expressed by the formula
E = mc2
The energy E is the mass (which varies with velocity) multiplied the square of the velocity of light.
Mass is converted into energy inside the Sun and stars; to keep the Sun shining, 44 million kilogrammes of mass are turned into energy every second. In most cases only a small fraction of mass can be converted into energy as the reactions are very inefficient, but when the elementary particles, electrons and positrons, collide they can turn completely into energy with 100% efficiency (see MASS-ENERGY EQUIVALENCE).
 |
 |
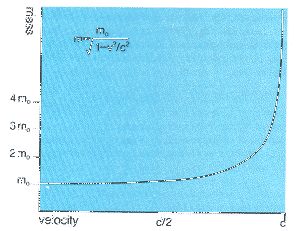
| As the velocity increases so does the mass
(m0 = rest mass). Although negligible at speeds below half that of light, the correction then increases rapidly |
By launching a rocket containing the most accurate clock available, a hydrogen maser, and comparing its rate by radar signals with a similar ground based clock, the gravitational redshift, or slowing down of clocks, can be measured. This experiment is currently being carried out |
General relativity
The General Theory of relativity, published in 1916, is a theory of
gravitation developed by Albert Einstein with the help of his mathematician
friend Marcel Grossman. Einstein realized that a gravitational field produced
effects equivalent to acceleration, and by studying the effect of acceleration
in special relativity was led to generalize the theory to include gravitational
fields. As acceleration affects the measurement of time and distance in special
relativity, so too do gravitational fields. As a result of this the geometry
found near gravitating bodies is not quite the classical geometry of the
ancient Greeks, called Euclidean geometry. For example, Pythagoras'
theorem (see MATHEMATICS) is no longer
exactly true due to the distortion of the measuring rods by gravitation.
Light rays no longer follow straight lines: a gravitational field causes them to bend and this bending of light from stars and radio sources has been measured, supporting Einstein's theory and defying the older theory of Newton. The slowing down of clocks in a gravitational field has also been checked and again is in good agreement with the prediction of general relativity. This prediction can be tested to very great accuracy by sending a clock up into space on a rocket and comparing its time with a similar clock on Earth. The theory also predicts slight changes in the motion of the planets in the solar system, particularly for the closest planet, Mercury, which again agrees with observations.
| Right: the most startling consequences of relativity theory are to be found deep in space. Some scientists believe that the violent disturbances observed in the centres of giant galaxies such as this one, M82, are the result of black holes or of relativistic motions. |  |
One of the more startling predictions of general relativity is that some stars will eventually collapse, becoming so small and having such a strong gravitational field that even light cannot escape from them. These black holes could then only be detected by the effect of their gravitational field and for all we know there could be very many such invisible objects in the Universe.
Reproduced from HOW IT WORKS p1963