
 |
How it works : Sine Wave |
The sine wave is a very important wave shape used extensively by both scientists and engineers. It is the waveshape observed in the simple harmonic motion executed by such devices as PENDULUMS and OSCILLATORS. Also it is closely associated with the properties of a circle and right angled triangles situated within a circle from which the sine and cosine of an angle can be determined (see MATHEMATICS).
A quality or property of something that alternates in the manner of a sine wave is said to he sinusoidal. The prongs of a tuning fork oscillate with sinusoidal motion, and the voltage waveform of the household mains supply is sinusoidal.
From circular to linear motion
The piston on a steam locomotive moves backwards and forwards with
near-sinusoidal motion because the piston is linked to the perimeter of the
drive wheel. With the train travelling at constant speed, the piston undergoes
reciprocal motion -speeding towards its central position, overshooting and
slowing down as it reaches the end, reversing and speeding back towards the
centre again, and so on.
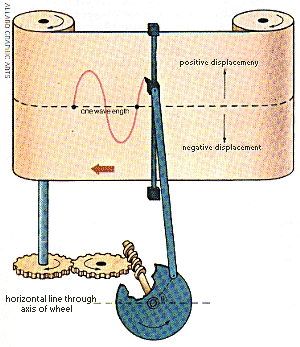 |
Consider a wheel and piston arrangement with a pen attached to the piston and touching a roll of paper that moves, via gears, according to the motion of the wheel. The shape produced on the paper is a sinusoid. With the pivot point on the wheel horizontally to the right of the wheel axis there is no vertical displacement of the pivot and the pen is at the centre of the paper. Turning the wheel anticlockwise moves the pivot upwards and to the left. The pivot and the pen are now displaced above their central positions. The pen recording is therefore a plot of vertical displacement against the angle of turn of the wheel (or distance along the paper). For the first 180° the displacement is above the line and labelled positive displacement; from 180° to 360°(completing the circular motion) the pivot is below the line and labelled negative.
After a 360° turn the pivot (and the pen) is back where it started and, continuing to turn the wheel, the pen recording waveform is repeated-that is, the basic sine wave shape is repeated. The sine wave is therefore said to be a periodic function and the length of one complete sine wave as measured on the paper is called the wavelength.
If the wheel is set spinning at constant speed the pen is said to be moving with simple harmonic motion. If the wheel is spinning at 10 revolutions per second (10 rps) then there are 10 repetitions of the basic sine wave shape per second. The frequency of oscillation of the pen is then 10 cycles per second-usually written as 10 hertz (10 Hz).
Sine and cosine functions
Mathematicians have given the sine wave its own function which labels and
describes its shape-this is the sine function. If the pivot on the
wheel is displaced by q from its original (zero
displacement) position then its vertical displacement is sin
q (assuming that the wheel has unit radius-for
example, one metre).
| The wave shape of sin and cos functions is repeated every 360° and the maximum displacement from the centreline is equal to the radius of the circle generating them. although,q is shown here measured in degrees it is more common to express angles in radians.360° is 2pradians (6.2832 radians). | 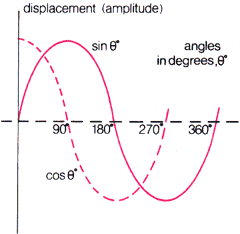 |
Plotting sin q on the vertical axis of a graph against increasing values of q (horizontally) produces a sine wave. The cosine of an angle q , cos q , produces an identical shape when plotted on a graph but the shape is shifted to the left by 90°; sin q and cos q are therefore complementary functions.
The relationships between sine and cosine functions can be more easily seen from the properties of a right angled triangle- which is where such functions are usually first encountered.
But the full significance of these functions is best demonstrated by placing this triangle inside a circle such that the hypotenuse (r) is a radius of the circle. Then x represents a horizontal displacement from the centre of the circle and y the vertical displacement.
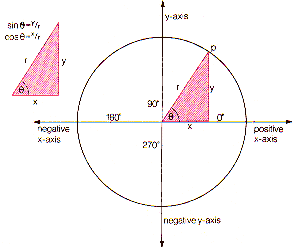 |
Clearly when q ° = 0, then y = 0 and sin 0° = 0 - a but at this same moment x = r and cos 0° = 1. When q = 90°, y = r so Sin 90° = 1, but x = 0, so cos 90° = 0. By suitable labelling of the axes as positive in one direction and negative in the opposite direction, sin q and cos q can be described for angles up to 360° .So, sin 180° = 0 and cos 180° = -1, sin 270° =-1 and cos 270° = 0 and finally sin 360° = sin 0 ° = 0 and cos 360° = cos 0° = 1. All values in between correspond to the shape of the sine wave.
From Pythagoras' theorem, the sides of a right angled triangle are related by the expression r2 = x2 + y2 . Dividing both left and right hand sides of this expression by r2 gives
1= (x/r)2 +(y/r)2
But x/r = cos q and y/r= sin q , and so
1= (cos q )2 + (sin q )2
This expression completely relates the sine and cosine values of an angle q °.
Reproduced from HOW IT WORKS p2110