Mathematics

Finding the fractal solution

Fractals are the abstract made gloriously visible. And now they're becoming useful shrinking images,diagnosing madness,even finding gold. It turns out that fractals are the very stuff of the universe

Naming the abstract: Benoit Mandelbrot
The man who lent his name to the most familiar of all fractals - the Mandeldbrot set - is a 70-year-old French mathematician and information theorist. He published his first work on fractals in 1977;the Set's subsequent popularity catapulted Mandelbrot from obscurity to international fame

A couple of years ago they were merely a craze, appearing everywhere from art galleries to T-shirts. Their intricate multicoloured whorls and spikes, at once bizarre yet strangely familiar, adorned album covers, posters and book jackets.
These extraordinary images were fractals, patterns within patterns within patterns, ad infinitum. They inspired artists to create images of alien landscapes and sent mathematicians soaring into exotic flights of theory to uncover their secrets and ramifications.
But now they are much more than just a buzzword for a bizarre abstract image. Their unique properties are being put to use in an astonishing range of applications.
Detectives are using them to track down stolen antiques. Geologists employ them to predict earthquakes and reveal buried minerals. Astronomers see them as a key to cosmic mysteries. Even psychiatrists are turning to fractals, believing that they may cast new light on mental illnesses.
Each of these applications focuses on the fundamental property of fractals: they are generated by repeating a simple pattern over and over again .Take the most famous of all fractals the so-called Mandelbrot Set, named after IBM mathematician Benoit Mandelbrot. Sometimes described as the most complicated object ever discovered the Mandelbrot Set has a literally infinite amount of detail - look closely, and you embark on an endless journey through spirals, spikes and zigzags. Yet all this detail can he summed up in a single, simple mathematical recipe Zn + 1 = Zn x Zn + C.
It takes some work to turn such a formula into an image, but with lateral thinking, you can convert it into a major moneyspinner. For example, if a small mathematical routine can be used to generate extremely detailed images, then extremely detailed images can be turned into a small mathematical routine.


The Mandelbrot Set is an infinite object that always looks similar but never repeats


And anyone with a computer knows the advantages of that. Just one full-colour image can easily mop up a megabyte of storage on a hard disk. Moving images are worse: one second of video can account for 30 megabytes. Compacting all this information has become one of the biggest challenges facing the computer industry. Which is where fractals come to the rescue. Virtually all raw data can be boiled down to some extent: the phrase "I sw a gd ftbll mtch n Strdy" is still recognisable, despite being "compressed" by over 25 per cent. The reason is that information invariably contains superfluous data which can be chopped out without any loss of content. In text, vowels can be removed. In images, repeated patterns can be identified.
For black and white pictures and text, data compression algorithms - that is, sequences of mathematical operations - find such patterns and change them into a shorthand form. Matching decompression algorithms can then be used to turn the shorthand back into the original.

Zn + 1 = Zn x Zn + C: the Mandelbrot secret

The simple mathematical equation above is responsible for the amazing, indeed neverending nature of the Mandelbrot Set - the infinite detail of which is apparent above as each picture zooms in on the last The equation is an "iterative" process - that is, an ongoing calculation in which each step is calculated from the previous step. In the case of the Mandelbrot Set, the numbers concerned are "complex" - ie, made up of two parts: a "real" part (eg, 1,2,3,4...), and an "imaginary" part (a real number multiplied by the square root of -1)
 If real numbers form a line (1,2,3, 4...) then complex numbers extend this line into a flat plane; this plane forms the canvas on which the Mandelbrot Set is painted. To draw a Set, take any complex number as a starting point. Run that number through the sequence above (where Zn is the complex number and C is a constant number). If the sequence heads toward zero, colour the point black. If its values bob about unpredictably, paint it another colour. And if it gets larger and larger, use yet another colour. Repeat for every point on the canvas, and the Mandelbrot Set will materialise before you.

Not only are cauliflowers, brains and landscapes fractal - the entire universe is too

Colour images are more problematic: there is a far wider range of colours than there are shades of grey. As a result, colour image compression algorithms so far developed either lose some information from the original or do not compress very tightly. In the late 1980s, however, British mathematician Mike Barnsley discovered fractals to be particularly good at capturing the essence of images.

Using maths to store pin-sharp pictures

Gecko

 These pictures of a gecko illustrate the advantages of "fractal" compression. 1: full size. 2: close-up of a conventional bitmap. 3: the more realistic close-up of a fractal image
Pictures stored on a computer are made up of thousands of individual dots, the colour of each defined by up to four data channels. As a result, storing a picture can take several megabytes. All image compression algorithms work by finding patterns which can be stored in a smaller space. For example, JPEG pictures are divided into areas containing different patterns. Fractal compression looks for fractal patterns, and stores only the mathematical description of each fractal, saving huge amounts of space.

Gecko Zoom

As mathematical recipes for fractals use far less memory than the original data, the images can be compressed by huge amounts - a factor of 100 or more. Better still, although working out the right fractals to compress a particular image might take a while, decompressing the image would be fast, as fractals are just mathematical formulae - bread-and-butter work to any computer. Thus no super-sophisticated hard- ware or software would be needed to "unpack" a fractal image.
But best of all, Barnsley saw that fractally stored images have an almost magical quality:just like the famous Mandelbrot Set, they can be magnified closely without losing detail; the formulae just go on generating image detail. Users of Microsoft's well-known Encarta CD-ROM encyclopaedia have Barnsley to thank for the compression of its 7000 images, reducing the CDs required from ten to two.
Fractal image compression is becoming commonplace. The Scottish Prisons Service is using it to store mugshots of thousands of prisoners in a computer database. If a prisoner escapes, the resulting fractal image is small enough to be sent to police forces via the ordinary telephone network and stored on a laptop computer. Meanwhile the Queen Mother Library of Aberdeen University recently used fractal compression to shrink a collection of 44,000 historic photographs down on to a single CD- ROM - a somewhat handier format than the five tonnes of magic lantern glass plates on which the images were originally stored.

Fractals may soon be used to expand the world's supply of oil and minerals. Geologists have found them to be a handy way of determining the extent to which layers of rock are broken up - a task which may prove invaluable for finding buried riches. At the heart of this technique is a feature again highlighted by Benoit Mandelbrot: fractals' curious "dimensionality". The term may be unfamiliar, but the concept isn't: a point is an object with no dimensions, while a line has one dimension, an area has two, and a solid has three. A fractal, in contrast, is an object occupying a strange hinterland between these whole-number dimensions. The greater the fractal dimension, the greater the "jaggedness" and convolution. Mandelbrot created a formula for calculating the dimensionality of a given fractal, along with some intriguing examples of its use. For example, the "jaggedness" of a coastline can be summed up by its fractal dimension: for the coast of Britain, it is around 1.25, while for the much smoother edges of South Africa it is around 1.0.
Geologists are now applying this fractal dimension to features such as faulting and veining, which have long served as clues to the existence of hidden deposits.

Vista Pro
How fractal landscapes repeat patterns of the natural world
Coastlines are jagged, their rocks are similarly jagged, and so on, all the way down to a grain of sand - and the same is true of all other natural phenomena. So the natural world is fractal. Because of this, programs using fractal mathematics can create extraordinarily realistic natural images; we produced the one above with a software package called vista Pro. A comparison with a scene from the "real world" (right) shows how close to reality fractally generated images are becoming

IRL

For example, a high level of quartz veins in drill cores have been linked to good quality gold seams. By counting the varying thickness of veins in such cores, David Sanderson and colleagues at Southampton University have been able to work out the fractal dimension of the veining - and link it to the likely concentration of gold in the area. They discovered that the lower the fractal dimension. the better the gold deposit.The explanation,they suspect, is that the thicker veining implied by the low fractal dimension has larger gaps through which water can flow. More water means a greater chance of tiny gold particles being carried in and trapped.

If this is true, measuring the fractal dimension of core samples may help exploration companies find other resources; the Southampton University team is currently using the same techniques in the search for tin and tungsten.
On a grander scale, fractal dimensions may also help seismologists give more reliable estimates of earthquake risks. In the 1930s, seismologists Beno Gutenberg and Charles Richter showed that the frequency of earthquakes follows a law: roughly speaking. big earthquakes are rare. medium ones fairly common, and feeble ones happen all the time. Earthquakes follow a "fractal" law and. just as the harder you look at the Mandelbrot Set the more detail you find, so the more sensitive your detection equipment the more earthquakes you will find.

By analysing earthquake data, scientists at the US Geological Survey have worked out the fractal dimension for quakes in the Los Angeles area. Publishing their results recently in Science, they concluded that there should be around six powerful quakes of magnitude 6.6 about every 250 to 300 years. The bad news for LA is that historical records suggest the area is behind on its quota... Fractals are even finding applications in deep space.

Cauliflower Vegetable Head
A cauliflower and a brain look remarkably alike- despite the fact that they develop in completely different environments and are made from different proteins.The reason? A fractal process underlies the growth of both
Nature grows fractal
You can find a fractal in your kitchen (or in your head). Take a close look at a cauliflower - perhaps slice it in two - and you will see a branching structure: each floret is like a miniature cauliflower - and if you look even more closely each floret is made up of still tinier replicas of itself. Similar self-repeating structures are found in the membrane of the brain - and in this case, how fractal the structure is appears to be linked to brain malfunctions like schizophrenia. other fractal geometries underlie most natural forms.		 Brain scan

Fractals suggest that Los Angeles is behind on its quota of earthquakes

Astronomers have found that galaxies tend to be gathered into clusters, and that these are themselves arranged into superclusters. In other words,the entire universe is fractal in nature - its fractal dimension is, apparently,about 1.2.
But fractals are also giving astronomers headaches. Many planets, stars and galaxies are known to have magnetic fields and for years astronomers thought they knew why. The rotation of these giant bodies swept up charged particles. so the theory went, with the swirling motion generating the magnetic field through a dynamo effect. Now this simple picture is threatened by the discovery that the loops of electromagnetic energy in galaxies may be fractal - that is, riddled with ever tinier twists which stop the magnetic field from building up. If true, astronomers will have to think again about the origin of cosmic magnetism.
Of all the new applications of fractals, the most surprising comes from Dr Ed Bullmore and his team at the Institute of Psychiatry in London. They have been measuring the fractal nature of the human brain - and found links with depression and schizophrenia.
The idea that the brain's shape may be connected to behaviour is not new. In the late 18th century, the Austrian physician Franz- Joseph Gall suggested a link between personality and skull shape. Known as phrenology, his was a nice idea, spoiled only by the fact that there is no correlation between the shape of the skull and any feature of the brain.
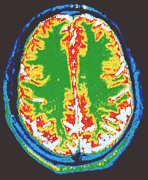
But the advent of medical scanning has breathed new life into Gall's idea. Scanning technology has been used to study the outer grey matter and the inner white matter of the brain. By measuring the fractal dimension ("jaggedness") of this boundary in dozens of patients. the team found that patients who suffer from manic depression have a more "jagged" grey-white matter boundary than normal people. In contrast. those with schizophrenia seemed to have particularly smooth boundaries.
The explanation behind this modern "phrenology" is a mystery, but it may yet prove useful. If so, it will be another triumph for the mathematical enigma whose properties were for so long just a toy.
Robert Matthews

INDEX

 Jul95