Mathematical Recreations

by Ian Stewart

The Topological Dressmaker

The floor was littered with bits of paper pattern, pins and snippets of cloth. Jemima Duddlepuck whistled as she worked on her new summer dress, while in a corner her dog, Pucci - who was rather lazy and very fat-snored happily. It was the first time Jemima had ever tried to make a dress with a lining. All that remained was to sew the two together, so that the seams ended up inside, between lining and dress, invisible from the outside.

She looked at the instructions. "Turn the lining inside out. Slip it over the dress. Machine around the neck and armholes. Turn the completed dress the right side out." Ever so gingerly, she machined around the armholes and the neck. The hems, of course, were left unattached. Done! Oh, it was going to be really nice. Jemima began to turn it inside out.

Funny. Was something stuck? No, if she turned it hack to the start, then everything seemed okay. But that final twist eluded her. Half an hour later she hurled the balled-up wad of material into the corner of the room and burst into tears. All that work for nothing.Then, having vented her frustration, she sat down to think the matter through. Jemima believed in learning from mistakes.

Had she made some parts the wrong shape? No, that wasn't likely. If you couldn't turn a slightly distorted dress inside out, then you couldn't turn a perfectly made one inside out either. Whether or not you could turn something inside out was a topological question-the answer didn't change if the object was continuously deformed. That meant two things. First, there was something wrong with the instructions in the pattern book-because whatever mistakes she'd made, they had to be very small ones. Second, there had to be a topological reason why the instructions were wrong.

What could she remember about topology? Well, there was the idea of topological equivalence. Two objects are "the same," or topologically equivalent, if one can be deformed continuously into the other. You can bend them and stretch them and shrink them and twist them, but you cannot cut them or tear them or glue bits together that weren't glued together to begin with. That was the basic idea-but what kind of things did topologists study? There was a lot of stuff about Klein bottles and Möbius strips, surfaces with only one side. But that wasn't likely to be relevant to problems about things with two sides. Then there was some other stuff about surfaces with holes. That was more likely to be useful.

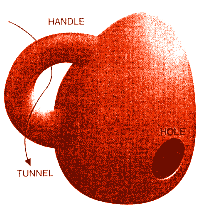
She recalled that "hole" is a rather ambiguous word in topology. For instance, people usually say that a donut - or torus - has a hole in it. But the hole isn't really in the donut at all. It's just a place where the donut isn't. Whereas if you take a car inner tube-also a torus - and cut out a patch of rubber, then you really do get a hole.

Some topological terminology

All right, she thought, I'll call the kind of hole you cut out with scissors a hole, and the kind where the surface just isn't I'll call a tunnel. One way to create a tunnel is to add a handle to a simpler surface [see illustration left]. By adding handles one at a time to a sphere, you first get a torus, with one tunnel through the middle. And then there's the two- handled torus, the three-handled torus and so on. She knew these were often called the two-holed torus and so on, but she wasn't keen to use the "hole" terminology without being very careful indeed what she meant.

Now, the instructions were to turn the lining inside out, so that its outside was on the inside; machine the neck and armholes; and then turn both lining and dress inside out so that the inside of the lining was next to the inside of the dress-no, the outside of the inside of the... no, the inside-out lin-. Oh, heck. Terminology for sides was going to be at least as much a problem as terminology for holes.

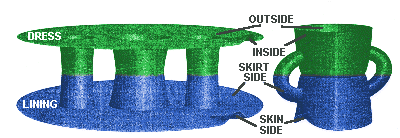
Start again. The dress has two sides: the outside, which is what everyone sees when you wear it, and the inside, which is what they don't see. The lining also has an inside and outside, but those are confusing words. So call the side of the lining that fits next to the skin the skin- side and the other side of it the skirt- side because it goes next to the dress. Well, as mnemonics go, those weren't too bad. It reminded her of George A. Strong's parody of Hiawatha :

When he killed the Mudjokivis,
Of the skin he made him mittens,
Made them with the fur side inside,
Made them with the skin side outside,
He, to get the warm side inside,
Put the inside skin side outside.

So the sides of the material, reading outward, have to end up in this order: skinside, skirtside, inside, outside And they had to be machined so that the stitches around the armholes and the neck were hidden between skirt- side and inside.

Topologically, both the dress and lining were equivalent to disks with three holes. The rim of each disk was the hem, and the holes were the two armholes and the neckhole. What the pattern book said was to place the disks so that the skinside was next to the outside; machine all three holes so that the stitches were on the skirtside/inside surfaces [see left illustration below] and then turn the whole ensemble inside out.

So the question was, what happened? Well, she thought, you can deform the whole ensemble topologically until it becomes a two-handled torus with two holes cut in it. (To see why, imagine sliding both ends of the two armhole tubes onto the neckhole tube and then bending the dress hem up and the lining hem down and shrinking them [see right illustration below].) So the problem becomes: Can you turn a two-handled torus inside out if there are two holes in it?

DRESS PLUS LINING is topologically equivalent to two disks, each with three holes, sewn together along three edges (left). This configuration in turn is topologically equivalent to a two- handled torus with two holes, hems of dress and lining (right).

It was kind of hard to think about, so Jemima started with something simpler.
Can you turn an ordinary torus inside out when one hole is cut in it? And the answer, of course, was yes. The idea was to flip the entire thing through the hole, but then the handle was like a tunnel bored into a sphere rather than a handle stuck on the outside. But you could imagine sticking a finger into the tunnel and straightening it. Then the part of the surface "outside" the tunnel is a rather distorted handle, which can be tidied up to look like a neater one. Then you got something that looked just like a torus again [see illustration below].

How to turn a torus inside out through one hole

So topologically, there was no difficulty.
She realized she could play the same game on the two-handled torus, too. She sketched a series of pictures of the process. First, turn the whole thing inside out through its holes, rather like reversing a sock (or in this case an ankle warmer because of the two holes). Then the two handles on the outside became two tunnels on the inside [see illustration below]. But then you can stick your finger into each in turn and pull it out to create a handle on the outside. And then all you have to do is twist each handle around, and you end up with the original ensemble, but turned inside out.

Hmm. You could do it topologically, then. Strange, because when she tried it with an actual dress, it didn't work.
Why not? Dresses, unlike topological spaces, can't be stretched or shrunk. They can be crumpled up and twisted around, though. It was possible that the material nature of the dress changed the answer, but she had a feeling that something both simpler and more fundamental was involved. She picked up the ruined mess from where she had flung it and smoothed it out. She could wriggle her arm between the various surfaces, and it really did seem as if there were three handles. But near the armholes and neckhole everything was confused, as if the lining and the dress were getting mixed up. There were three handles, all right, but they just weren't in the right places.

TO TURN the ensemble inside out, reverse the whole thing. Pull the tunnels out to form handles. Twist the handles into correct position. Note, however, where seams end up.

Aha! She'd forgotten to think about the seams. They had to end up in the right places, neatly separating dress from lining. But did they?
She drew the seams on her pictures. No, they didn't. When the surface was stretched, to create the handles from the tunnels, and then twisted to put the handles in the right place, all three seams ended up in completely the wrong places. (E. C. Zeeman of the University of Oxford has proved that there is no way to make them end up in the right places.) So that was the topological obstruction to turning the ensemble inside out. You couldn't do it if the seams had to end up where they started.

And that gave her another idea. Maybe the ensemble wasn't ruined after all. She could unpick the stitches and try to find some other method of making the seams. She would be on her own, though - obviously, the instructions on the pattern were crazy.
Jemima unpicked one armhole, then the other. She was about to start on the neck when she had another thought. Topologically, each hole was just as good as the others. You had to start by machining some seam. The neck was as good a place to start as any.
Let's experiment, she mused. She pulled the lining inside the dress, skin- side inside, then skirtside next to inside of dress, then the outside of the dress- well, outside.

Great! She even found that she could poke the arms of the lining down the arms of the dress, just where they ought to end up. The only trouble was, she couldn't machine around the seam; the stitches would be on the outside.
So turn just the arm inside out. She pulled the arm of the lining inside the dress, turning it inside out like a sock. Then she did the same with the arm of the dress. She burrowed into the ensemble from the hem end, flashlight in hand. It certainly looked as if the arm could be restored to its correct position. All she had to do was push the sewing machine up inside the ensemble and then-

Stupid. Sheepishly, she backed out of the heap of crumpled cloth. She reached in through the neck and pulled the sleeve out into the open. She ran the seam through the machine, then turned it inside out and back to its proper position. Now the dress really was finished. She tried it on and pirouetted in front of the mirror. Brilliant!

I ought to write a book about this, she reflected. Topology for Tailors. I could throw in all the party tricks, like taking off your vest without removing your jacket.
By now her mind was in overdrive. Suppose you were a Martian with 17 arms. How many hems would be needed to make a Martian ensemble, dress plus lining? Seventeen? No, just two. Use the same trick of machining the neck only and then dealing with each arm in turn by pulling it through the neckhole, inside out. Unfortunately, there weren't any Martians. So she wouldn't get to try it out-"Pucci, stop that, your nose is all wet!" She pushed the little dog gently away.

Say, Pucci had four "arms," and its tail could poke out through the hems. Jemima took the dog's measurements, tut-tutting at the figures for the waist- line. She cut shapes from remnants of the cloth, whistled, sewed, twisted and turned. Yes, even with four "arm" holes, the method worked fine. Now to see if the dress fitted the dog.
It fitted, in the sense that the measurements were okay. But fat dog into small hole won't go.
In the real world, there are nontopological constraints.

SCIENTIFIC AMERICAN July 1993 File Info: Created  2/5/2001 Updated 17/10/2000 Page Address: http://www.fortunecity.com/emachines/e11/86/klein2.html