by Ian Stewart
Counting the Cattle of the Sun
Some problems are too big to solve by trial and error
In his 1917 book Amusements in Mathematics, English puzzle maker Henry Ernest Dudeney described a fanciful problem based on the Battle of Hastings, the famous confrontation in 1066 between the Saxons under King Harold and the Normans under William the Conqueror. According to Dudeney, an ancient chronicle of the battle stated:
 |
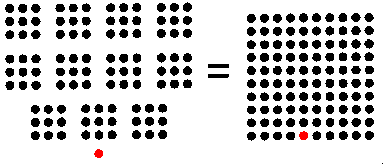| SMALLEST SOLUTION: Army of 99 soldiers (black dots) and King Harold (red dot) can be arrayed in 11 squares led by Harold (left) or in one big square including Harold (right). |
"The men of Harold stood well together, as their wont was, and formed sixty and one squares, with a like number of men in every square thereof.... When Harold threw himself into the fray the Saxons were one mighty square of men." What, asked Dudeney, is the smallest possible number of men in King Harold's army?
Mathematically, we want to find a perfect square that, when multiplied by 61 and increased by 1, yields another perfect square. That is, we want integer solutions of the equation y2 = 61x2 + 1. This is an example of a Pell equation, mistakenly named after an obscure 17th-century English mathematician whose contributions to the field were not original. Equations of this general kind-in which 61 can be replaced by any nonsquare positive integer-always have infinitely many solutions. The technique for calculating the solutions is called the continued-fractions method, which can be found in most number theory textbooks.
As a warm-up, let's take a look at the lesser-known Battle of Brighton, where King Harold's men formed 11 squares, all else being unchanged [see illustration above]. Now the equation is y2 = 11x2 + 1. A little trial and error reveals the smallest solution: x = 3, y = 10.
Trial and error, though, will not solve Dudeney's puzzle-except perhaps on a computer-because the smallest solution is x = 226,153,980, y = 1,766,319,049. Solutions of the Pell equation y2 = Dx2 + 1 vary wildly with D, the positive non- square coefficient. The "difficult" values of D below 100-that is, those that yield a smallest solution for x that is greater than 1,000-are D = 29, 46, 53, 58, 61, 67, 73, 76, 85, 86, 89, 93, 94 and 97. By far the most difficult value is 61, 50 Dudeney chose wisely. With a bit of effort you should be able to find out what happens for D =60 and D =62, on either side of Dudeney's cunning 61 (the answers are provided at the end of the column).
Mind you, Dudeney could have made the puzzle a lot harder: with D = 1,597, the smallest solutions for x and y are ap proximately 1.3 x 1046 and 5.2 x ~ And D = 9,781 is even worse.
The
Pell equation is also the key to solving a much more famous puzzle called
the Cattle of the Sun. In 1773 German dramatist Gotthold Ephralm Lessing
discovered a manuscript containing the problem, which was expressed in the
form of a poem: 22 elegiac couplets supposedly written by Greek mathematician
Archimedes of Syracuse around 250 B.C. and sent in a letter to Eratosthenes
of Cyrene, the chief librarian at Alexandria. It begins, "If thou art diligent
and wise, O stranger,compute the number of cattle of the Sun,
who once upon a time grazed on the fields of the Thrinacian isle of Sicily."
The cattle of the sun are mentioned in Homer's Odyssey. The epic poem claimed that there were 350, but Archimedes had a larger figure in mind. According to his puzzle, the herd is divided into white bulls (W), black bulls (B), yellow bulls (Y) and dappled bulls (D), together with the corresponding varieties of cows (w b, y and d). The number of cattle is specified by seven easy-to-satisfy conditions and two difficult ones. The easy conditions can be expressed as seven equations relating the eight variables [see illustration on left]. The first difficult condition is that the total number of white and black bulls (W + B) must be a perfect square. The second is that the total number of yellow and dappled bulls (Y + D) must be a triangular number-that is, it must equal a sum l+2+3+...+m, where m is a positive integer.
The first seven conditions boil down to a single fact: all eight unknowns are proportional to one another by fixed ratios. Unraveling the equations, we find that the solutions are (for any integer n):
W =10,366,482n, B = 7, 460,514n,
Y = 4,149,387n, D = 7,358,060n,
w = 7,206,360n, b = 4,893,246n,
y =5,439,213n, d = 3,515,820n
The challenge now is finding the smallest n that satisfies the two difficult conditions. In 1830 German mathematician J. F. Wurm solved a simpler version of the problem, which ignored the condition that W + B be a perfect square. The condition that Y + D be a triangular number leads, after some algebra, to the requirement that 92,059,576n + 1 be a square. If we plug in the smallest value of n that fulfills this requirement, the total number of cattle is a mere 5,916,837,175,686.
Wurm's equation, however, has infinitely many solutions for n, and among them we can seek the smallest that also satisfies the condition that W + B be a perfect square. In 1880 A. Amthor -another German mathematician-proved that n must equal 4,456,749m2, where m satisfies a Pell equation: 410,286,423,278,424m + 1 = a perfect square. The continued-fractions method can now be used to find the smallest such m. The calculations were too intractable for Amthor to complete, but he determined that the total size of the herd is a number with 206,545 digits, the first four of which he was able to identify. Between 1889 and 1893 the Mathematical Club in Hilisboro, Ill., calculated the first 32 digits, 30 of which turned out to be correct. The first complete solution was found in 1965 by mathematicians at the University of Waterloo in Ontario. The list of all 206,545 digits was published in 1981 by Harry L. Nelson. He used a CRAY-1 supercomputer, and the calculation took 10 minutes.
There, until recently, the matter rested. Today's mathematicians, however,
have ultrafast computers that can do arithmetic to hundreds of thousands
of digits in the blink of an eye.Ilan Vardi of Occidental College found that
the computer algebra package called Mathematica could redo all the above
analysis in a few seconds. Pushing a little harder, he discovered that
Mathematica could also produce an exact formula for the size of the herd;
previously, mathematicians had not suspected that such a formula existed.
On a Sun work station-an appropriate choice given the owner of the cattle-the
computation took an hour and a half. The details are described in Vardi's
arti le "Archimedes' Cattle Problem," in American Mathematical Monthly
(April 1998). The upshot of all this is that the total number of cattle
is the smallest integer that exceeds (p/q)(a + b
Ö4,729,494)4,658, where
p = 25,194,541
q= 184,119,152
a = 109,931,986,732,829,734,979,866, 232,821,433,543,901,088,049
b = 50,549,485,234,315,033,074,477,819, 735,540,408,986,340.
Scholars debate whether Archimedes actually posed this problem. The consenus view is that he did, although he may not have written the poem. What is more certaln is that Archimedes could not have solved the problem-it is simply too big. Calculation by hand would have taken far too long. Did Archimedes even know that a solution existed? Probably not. He was certainly clever enough to figure out that some type of equation was required, but it seems unlikely that he could have known that such an equation would always have a solution. The moral of the story: Beware of Greeks bearirig puzzles.
ANSWERS:For D = 60, x = 4, y = 31
For D = 62, x= 8, y= 63
READER_ FEEDBACK |
 |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
SCIENTIFIC AMERICAN April 2000 File Info: Created 12/10/2005 Updated 5/5/2009 Page Address: http://members.fortunecity.com/templarseries/cattle.html