

by Ian Stewart
Tales of a Neglected Number
Last month I described the mathematical sculptures of Alan St. George, who
often makes use of the well known
"golden number". The catalogue of his Lisbon
exhibition mentions a less glamorous relative, referring to a series of articles
in which "the architect Richard Padovan revealed the glories of the 'plastic
number.' "
The plastic number has little history, which is strange considering its great
virtues as a design tool, but its provenance in mathematics is almost as
respectable as that of its golden cousin. It doesn't seem to occur so much
in nature, but, then, no one's been looking for it.
 |
| A Pearly Nautilus and it's logarithmically spiral shell. [Image:"Life on Earth" D.Attenborough p46] |
For purposes of comparison, let me start with the golden number: q =1 + 1/q
= 1.618034, approximately. The golden number has close connections with the
celebrated Fibonacci
numbers. This series can be illustrated by a spiralling system of squares
[see upper illustration on this page]. The
initial square (in gray) has side 1, as does its neighbour to the left. A
square of Side 2 is added above the first two, followed in turn by squares
of side 3, 5, 8, 13, 21 and so on. These numbers, each of which is the sum
of the previous two, form the Fibonacci series.
The ratio of consecutive Fibonacci numbers tends to the golden number. For
example, 21/13 = 1.615384.
This fact is a consequence of the rule for generating Fibonacci numbers:
for large numbers, it leads to the equation q=1 + 1/q . If a quarter circle
is added inside each square, the arcs fit together into an elegant spiral.
This spiral is a good approximation to the so-called logarithmic spiral often
found in nature, such as in the shell of a
nautilus mollusc. [Ref: I.Stewart "Nature's Numbers"
p88] Successive turns of the spiral grow at a rate approximately equal to
the golden number.

That's the golden tale: now for the plastic one. We start with a similar
diagram, but composed of equilateral triangles [see lower
illustration on this page]. The initial triangle
is marked in gray; successive triangles are added in a clockwise direction.
The spiral generated is again roughly logarithmic. In order to make the shapes
fit, the first three triangles all have side 1. The next two have side 2;
then the numbers go 3, 4, 5, 7, 9, 12, 16, 21 and so on. Again there is a
simple rule of formation: each number is obtained by skipping the previous
one and adding the two before that. Let me call this sequence the Padovan
Sequence in honour of Richard Padovan. (It is curious that Padova is the
Italian form of Padua, and Fibonacci was from Pisa-roughly 100 miles from
Padua.)
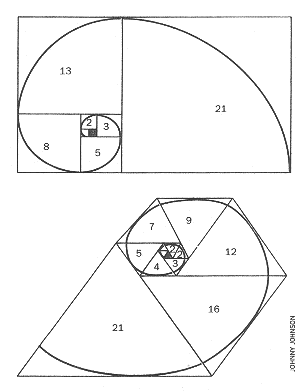 |
| SPIRALING SYSTEMS illustrate the Fibonacci numbers (top) and the Padovan sequence (bottom) |
In algebraic form the generating rules for the Fibonacci sequence F(n) and
the Padovan sequence P(n) are given as follows:
F(n+ 1) = F(n) + F(n - 1) where F(0) = F(1) = 1,
and
P(n + 1) = P(n - 1) + P(n - 2) where P(0) = P(1) = P(2) =1.
The family resemblance is very apparent. The plastic number, which from now
on I shall call p and whose approximate value is 1.324718, arises as the
limit of the ratio of successive Padovan numbers-just as the golden number
arises from the Fibonacci sequence. The formation rule leads to the equation
p = 1/p + 1/p2, or equivalently p3 - p - 1 = 0; the
number p, is the unique real solution of this equation.
The Padovan sequence increases much more slowly than the Fibonacci sequence,
because p is smaller than q. There are many interesting patterns in the Padovan
sequence. For example, the figure shows that 21 = 16 + 5, because adjacent
triangles on the same edge have to fit together. Thus, an alternative rule
for deriving more terms for the sequence is P(n + 1) =P(n) + P(n - 4).
Some numbers, such as 3, 5 and 21, are both Fibonacci arid Padovan. Are there
others? If so, how many, and is that count finite or infinite? Some Padovan
numbers, such as 9, 16 and 49, are perfect
squares-are there others? The
square roots here are 3, 4 and 7-also
Padovan numbers. Is this a coincidence or a general rule? These and many
other questions deserve further study.
Another way to generate the Padovan numbers is to mimic the use of squares
for Fibonacci numbers, but with cuboid structures, boxes with rectangular
faces. Now we get a kind of three-dimensional spiral of boxes
[see illustration]. Start with a cube of
side 1, placing another adjacent to it. The result is a 1 x 1 x 2 cuboid.
On the 1 x 2 face, add another 1 x 1 x 2, getting a 1 x 2 x 2 cuboid. Then
on a 2 x 2 face, add a 2 x 2 x 2 cube, to form a 2 x 2 x 3 cuboid overall.
To a 2 x 3 face, add a 2 x 2 x 3 to get a 2 x 3 x 4 overall, and so on. Continue
the process, always adding cuboids in the sequence east, south, down, west,
north and up. At each stage the new cuboid formed will have as its sides
three consecutive Padovan numbers.
Moreover, if you connect successive square faces of the added cuboids by
straight lines, you get a spiral. It even turns out that this spiral lies
in a plane. St. George has based a sculpture on this construction, made from
rigid rods connected by drilled balls at their corners. (What diagram does
the intersection of the system of cuboids with this plane form?)
A sequence with the same rule of formation, but starting with different values,
was studied in 1876 by the French mathematician Édouard Lucas. In
1899 his ideas were further developed by R. Perrin, and the sequence is now
known as the Perrin sequence A(n). The Perrin numbers differ from the Padovan
numbers in that A(0) = 3 ,A(1) =0 and A(2) = 2. Again the ratio of consecutive
Perrin numbers tends to become p, but Lucas noticed a more subtle property.
Whenever n is a prime number it
divides A(n) exactly. For example, 19 is prime, A(19) = 209 and 209/19 =
11.
This theorem provides a curious test for a number to be composite-that is,
not prime. For instance, when n = 18, we have A(18) =158 and 158/18 = 8.777,
which is not a whole number. Therefore, 18 must be composite. So we can use
Perrin numbers to test for nonprimality: any number n that does not divide
A(n) is composite.
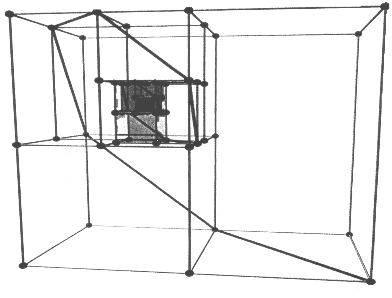 |
SPIRALING CUBOIDS also form Padovan numbers |
If n divides A (n), must n always be prime? This does not follow from Lucas's
theorem-any more than "if it rains, then I get wet" implies if I get wet,
then it rains." (I might have fallen into a pond on a perfectly dry day.)
Still, it is a fascinating open question. Nobody has ever found a composite
n that divides A(n), but nobody has shown that such numbers-known as Perrin
pseudoprimes do not exist. In 1991 Steven Arno of the Supercomputing Research
Center in Bowie, Md., proved that Perrin pseudoprimes must have at least
15 digits. I would be delighted to hear of any more recent progress.
The conjecture that no Perrin pseudoprimes exist is important, because the
remainder on dividing A(n) by n can be calculated very rapidly. If the conjecture
is true, this remainder will be 0 if and only if n is prime, thereby providing
a speedy primality test. (Indeed, in 1982 William W. Adams and Daniel Shanks
of the University of Maryland found a way to calculate this remainder in
log n steps.) Thus, the conjecture should have useful applications to
secret codes, which nowadays often hinge on properties
of large primes.
Just like its glittering golden cousin, the plebeian plastic number generates
rich spirals of ideas.
Home-grown sea shells reveal nature's trick
THE world's smallest beach is in a laboratory in Canada. Chemists at the University of Toronto have found a way to create tiny shells with dimensions about the thickness of a human hair. These shell mimics could help to explain how marine organisms turn minerals from the sea into the beautiful whorls and spirals of their hard body parts. Sea creatures use calcium carbonate dissolved in seawater to make their shells. They cement these mineral building blocks together with organic polymers such as proteins, polysaceharides and phospholipids on the membranes of their cells. The organic polymers act as templates for the crystallisation process, but it is still a mystery how animals produce shells that follow mathematical functions such as logarithmic and Archimedean spirals. Chemists interested in biomineralisation have been able to synthesise shell-like materials for a decade or more ("Crystal engineering: the natural way", New Scien tist, 10 March 1990, p 42). But producing the three-dimensional structure of shells is more difficult. Now Geoffrey Ozin and his colleagues at the University of Toronto and Neil Coombs of Imagetek Analytical Imag ing, also in Toronto, report creating a ran dom collection of tiny shells on a synthetic beach (Advanced Materials, vol 9, p 662). The Canadian team used tetraethyl silicate, a material based on silica-the stuff of sand-in place of calcium carbon ate, and a soap-like surfactant called cetyltrimethylammonium chloride instead of the organic polymer templates. They mixed these in water with a little hydrochloric acid to catalyse the reaction and, over the course of a week, shell-like structures emerged spontaneously. With help from Fred Neud, also at the University of Toronto, the scientists took scanning electron micrographs of the shells as they formed. Their pictures reveal numerous spirals and what Ozin describes as "gyroid" structures, where two spirals are joined base to base. The images also show that the synthetic shells have corrugated ridges, channels and protuberances- much like their natural counterparts. "We have the first recorded synthetic examples of shell shapes and a good idea of how they form," says Ozin. He believes each tiny shell begins life as a hexagonal, cylindrical liquid crystal which then evolves into a spiral or gyroid form as the silica-based molecules are cemented together with varying degrees of curvature. The early stages of real shell growth could be seeded from similar structures, says Ozin. Steven Mann from the University of Bath, who is also working on creating inorganic structures, thinks the work could be very important. "Inorganic compounds usually form regular geometrical crystalline shapes," he says. "Ozin seems to have succeeded in making a huge range of shapes from inorganic compounds." Mann believes that Ozin's technique has the potential to create chemicals with specific shapes rather than random grains of powder. This would revolutionise areas as far afield as catalysis and separation of bacterial cells for analysis. It could even make surgical implants more biocompatible. |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
SCIENTIFIC AMERICAN June 1996 File Info: Created 18/6/2000 Updated 15/03/2007 Page Address: http://members.fortunecity.com/templarseries/padovan.html