Survival of the Fittest Bits
RICK L. RIOLO
In Darwinian terms, life is a struggle in which
only the fittest survive to reproduce. What has proved successful to life
is also useful to problem solving on a computer. In particular, programs
using so-called genetic algorithms find solutions by applying the strategies
of natural selection. The algorithm first advances possible answers. Then,
like biological organisms, the solutions "cross over," or exchange "genes,"
with every generation. Sometimes there are mutations, or changes, in the
genes. Only the "fittest" solutions survive so that they can reproduce to
create even better answers [see"Genetic Algorithms"
by John Holland].
One way to understand how genetic algorithms work is to implement a simple
one and use it in some experiments. I chose the C language for my algorithm,
but any other computer language would do as well. It took me two days to
complete the version described here. I spent the most time by far writing
the utilities to make the program easy to run, to change parameter settings
and to display the population and statistics about its performance.
I recommend developing a genetic algorithm in two steps. First, write utilities
(some are described below) to track the population's average fitness and
the most fit members of each generation. Your version should generate random
populations of individuals and have subroutines to assign fitness. The program
should also display the individuals and their fitnesses, sort by fitness
and calculate the average fitness of the population. Second, add subroutines
to implement the genetic algorithm itself. That is, your program should select
parents from the current population and modify the offspring of those parents
through crossover and mutation.
In writing a genetic algorithm for the first time, I found it best to use
a simple problem for which I know the answer. This approach made it easier
to debug and to understand the algorithm. Adjusting it for more complex problems
is not too difficult.
I chose the problem of finding the optimum value of the function f(x)=
x+ sin |(32x) |. I limited the values of x (the domain)
to between 0 and p (I am working in radians,
where p = 180 degrees.) Thus, this
function has 32 regular oscillations added to the straight line f(x)=
x[see illustration below]. Because f(x) is always positive,
it can be used directly as a measure of fitness. The goal is to find an
individual string (a value of x) that yields the largest f(x).
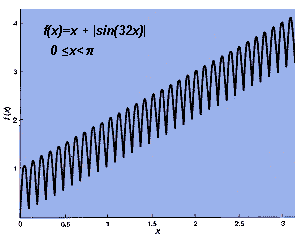 |
| FITTEST SOLUTION of f(x)= x+ sin |(32x)| is the value of x that yields the highest f(x). The answer is x = 3.09346401 (in radians), represented by 1111110000010100 |
The first step is deciding how to represent structures from
the domain in a form your genetic algorithm can process. I represented the
values of x as binary strings, as described in Holland's article.
For my initial experiments, I chose the length, L, of my strings to be 16
bits (L= 16). I thus have 2L= 216= 65,536 possible
values of x. (Increasing the length of the string improves the precision
of the solution.) I assigned these 2L string values to values
of x: I let the string 0000000000000000 represent x= 0,
0000000000000001 to be x = 1(p
/2L), 0000000000000010 to be x =
2(p /2L), and so on, all the
way to 1111111111111111, which represents the maximum value of the domain,
x= (2L - 1) (p /2L)
=p - p/
2L . (The value of p itself
is excluded because there is no string left to represent it.) To test your
intuition, what value of x does the string 1000000000000000
represent?
In short, the binary strings represent 2L values of x that are
equally spaced between 0 and n. Hence, as the algorithm searches the space
of binary strings, it is in effect searching through the possible values
of x. The C fragment (the mapping
algorithm) shows one way to implement this mapping from a binary string,
which is stored as a char array in C. For example, it will map 1000000000000000
onto (approximately) p/2. The fitness of
an individual binary string S is just f(x), where x =
MapStringToX(S).
Given this mapping from binary strings to the domain of f(x), it is
instructive to map schemata, or target regions, as specified by Holland.
For example, the schema 0*************** consists of all the strings that
start with 0. The * is the "don't care" place holder: it does not matter
whether it is 0 or 1. The schema 0********** maps into the first half of
the domain-that is, between 0 and p/2.
The schema 1*************** corresponds to the other half, between
p/2 and
p. For the function f(x), the average
value of f(x) over 1*************** is greater than that over
0************** Thus, in a random population of strings, you should find
that the average fitness of individuals in the former region is greater than
that of members in the latter.
My implementation includes some subroutines that track individuals in any
schemata specified by the user (for example, all strings that start with
1 or all that end in 001 and so forth). At each generation, the program will
count the number of individuals in the population that are members of each
region. It will also calculate the average fitness of those individuals,
thus explicitly estimating the fitness of the regions.
To further hone your intuition, try mapping some other schemata into the
domain x and examine the random individuals that fall into those regions.
Can you specify schemata that partition each oscillation in f(x) into
eight contiguous regions? What is the average fitness of individuals in each
region?
Once you are confident the first version of your program is working, you
should add the subroutines that implement the heart of the genetic algorithm.
The algorithm I used appears on the next page.
The EvaluatePopulation subroutine simply loops over all the individuals in
the population, assigning each an f(x) value as a measure of fitness.
The DoTournamentSelection subroutine conducts a series of tournaments between
randomly selected individuals and usually, but not always, copies the fittest
individual of the pair (i,,j) to NewPop. A sample tournament selection algorithm
appears on the next page. In the algorithm, URand01 returns a (uniformly
distributed) random value between 0 and 1. The net effect is that more fit
individuals tend to have more offspring in the new population than do less
fit ones. You may find it useful, nonetheless, to copy the fittest individual
into the new populations every generation.
Note that if URand01 is greater than 0.75, the selective pressure will be
greater (it will be harder for less fit strings to be copied into NewPop),
whereas a smaller value will yield less selective pressure. If 0.5 is used,
there will be no selective pressure at all.
The ModifyPopulation subroutine should randomly perform the crossover operation
on some of the pairs in NewPop), a typical crossover rate is 0.75 (that is,
cross 75 percent of the pairs). I used the "single point" crossover operation
described in Holland's article. My version also mutates a small, randomly
selected number of bits in the individual strings, changing the value from
1 to 0, or vice versa. A typical mutation rate is 0.005 per bit-in other
words, each bit has a 0.005 chance of being mutated.
Once the implementation is complete, you can begin to run experiments. Try
starting the system with a random population of 200 individuals and run it
for 50 generations, collecting statistics on how the average fitness changes
and noting the highest individual fitness found at each generation. You might
compare the results you get with different population sizes and with crossover
and mutation rates. I found it best to compare average results from several
runs started with different seeds of the random number generator.
One especially useful experiment for understanding the dynamics of how
populations evolve is to track the individuals in the eight regions that
partition the 32 oscillations of f(x), to which I referred earlier. The regions
are defined by the schemata *****000********, *****001********and so on,
to *****111********. Notice that *****0111******** and *****100******** occupy
the center part of each peak, which includes the points of highest fitness.
In an initially random population, there should be approximately equal numbers
of individuals in each of the eight schemata. As the genetic algorithm runs,
you should see, on average, more individuals in the two center schemata than
in the other six. This result happens even though many members of the center
schemata map into low values of x and so have low fitnesses. The reason
is that the average fitness in the center schemata is higher than that in
the others.
Using these eight schemata, I tried to track how well the algorithm can bias
its search for individuals of higher fitness. I set up my program to record
at each generation the number of individuals in each schema, the average
fitness of the individuals in those regions and the average fitness for the
population as a whole. The theorems mentioned in Holland's article predict
that the number of individuals in regions with an estimated average fitness
above the population average should increase and the number of those in regions
having below-average fitness should decrease.
For a population of 400, a crossover rate of 0.75 and a mutation rate of
0.001, the program confirmed the predictions about 67 percent of the time.
I found that the greater the mutation and crossover rates and the smaller
the population size, the less frequently the predictions were confirmed.
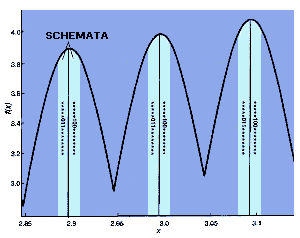 |
| TWO SCHEMATA occupy the central regions of each peak in f(x). They include the points of highest fitness. Only the last three peaks are illustrated. |
These results make sense, I think, because higher mutation
and crossover rates disrupt good "building blocks" (schemata) more often,
and, for smaller populations, sampling errors tend to wash out the predictions.
After your genetic algorithm has run for many generations, you will probably
notice that most of the population consists of very similar, if not identical,
strings. This result is called convergence and occurs because the genetic
algorithm pushes the population into ever narrower target regions. Often
the population will converge to an individual that is not the optimal one.
Essentially, the algorithm has gotten stuck on a local optimum. Convergence
can he particularly debilitating, because it means that crossover will not
contribute much to the search for better individuals. Crossing two identical
strings will yield the same two strings, so nothing new happens.
Finding ways to avoid inappropriate convergence is a very active area of
research. One possible mechanism involves biasing the selection process to
keep the population diverse. In essence, these mechanisms encourage individuals
to occupy many different regions in the domain in numbers proportional to
the average value associated with those regions, much as different species
inhabit niches in natural evolution.
Of course, you can apply the genetic algorithm to problems other than optimizing
functions. It took me about four hours to modify the program described here
to create a version in which the individuals represent strategies for playing
a form of the Prisoner's
Dilemma. In this game, two prisoners face a choice: cooperate with the
other (by remaining silent about the crime) and receive a three-year sentence,
or try to get off free by "defecting," or squealing. Unfortunately, you do
not know what the other player is going to do: if you cooperate and he defects,
then you get a 10-year sentence and he goes free. If you both defect, then
you both get seven years.
My modified genetic algorithm explored the strategies involved in playing
the game many times with the same opponent. Each individual's binary string
represents two numbers (p, q), where p is the probability the individual
will cooperate if the opponent cooperated on the previous play and q is the
probability of cooperation if the opponent had defected. For instance, the
strategy (1,0) is tit for tat, and (0.1,0.1) is approximately the "always
defect" approach.
The genetic algorithm generates some very interesting dynamics in the evolution
of populations of such strategies, especially if each individual's binary
string also contains some bits that specify an arbitrary "tag." Another set
of bits could then indicate the propensity of the individual to play only
with those that have a similarly tagged string. In effect, the population
can evolve individuals that recognize external "markings" (the tags) associated
with tit-for-tat players. Thus, they can prosper by looking for cooperative
individuals and by avoiding defectors.
From relatively simple gene structures, complicated evolutionary dynamics
may emerge. For instance, mimicry and other forms of deception may evolve:
a defector could have a tag associated with cooperators. With some imagination,
you can construct other simple gene structures and use the genetic algorithm
to coax complex evolution out of your computer.
For a copy of the optimization program (written in C language), please
write to: The Amateur Scientist, Scientific American, 415 Madison Avenue,
New York, NY10017-1111.
MAPPING ALGORITHM-allows binary strings
to represent values of x
(Note: the compiler defines M_Pl as p)
double scalefactor = (double) M_Pl / pow ((double) 2.0,(double) L);
double MapStringToX (char *S)
{/* put bits from S in rightmost end of r and move them left */
int i, r;
> for ( i = r = 0; i < L; ++i, ++S){
r << = 1: /* shift bits left, place 0 in right bit */
if ( *S == '1') /* if S has a 1,then... */
++r; /* change rightmost bit to 1 */
}
return ((double) r * scalefactor );
}
BASIC GENETIC ALGORITHM-performs crossover, mutation and selection
operations repeatedly
/* create structure to store the populations */
struct PopStr {
char Genome[L + 1]; double Fitness;
}Pop[PopSize], Newpop[PopSize];
/* implement algorithm */
GenerateRandomPopulation ( Pop);
EvaluatePopulation ( Pop );
while ( Not_Done ) {
DoTournamentSelection ( Pop, NewPop);
ModifyPopulation (NewPop);
Switch ( Pop, NewPop);
EvaluatePopulation ( Pop);
}
TOURNAMENT SELECTION ALGORITHM-selects for and copies the more fit
individuals into the next generation
while ( NewPopNotFull ) {
/* pick two individuals from Pop at random */
i = random ()% PopSize; j = random ()% PopSize;
/* return a random value between 0 and 1 */
if (URand01()<0.75)
copy the most fit of Pop[i], Pop[j] to NewPop
else
copy the least fit of Pop[i], Pop[j] to NewPop
}