When electrons go with the flow
|
Remove the obstacles that create electrical resistance, and you get ballistic
electrons and a
quantum surprise
Peter Main
At its most basic level, a computer is little more than a
box of interconnected switches. Its speed of operation, which in turn governs
the amount of information it can handle, is determined by the speed at which
an electrical signal can be transferred between the switches and the speed
of the switches themselves. The search for ever faster computers has led
to an inexorable decrease in the size of electronic components; modern techniques
allow the routine fabrication of devices and interconnections on scales less
than one millionth of a metre, smaller than the wavelength of light. Even
at this level, though, size is unimportant in terms of the physics controlling
devices. The operation of a transistor a millimetre in size is unchanged
if it is scaled down a hundredfold.
But even the ancient Greeks knew that things cannot be made
smaller indefinitely. Eventually, if components are made sufficiently small,
it is no longer valid to think of the electrons which carry the electric
current in Newtonian terms, as a mass of tiny
billiard balls. If we consider a device so small that it contains only one
or two electrons, we have to treat the electrons as
quantum mechanical particles which behave in
counter-intuitive
ways. Far from being a problem, this raises the possibility of using
properties such as the quantum character of the
electrons to develop a whole new regime of electronics based on a completely
different physics. The vast amount of research devoted to this aim over the
past decade or so, driven by the fabrication technology; has also forced
physicists to rethink the way they look at the conduction of electricity.
In 1827 the German scientist Georg Simon Ohm made the first
step in understanding electrical conduction in solids with the formulation
of his famous Ohm's law. The law, familiar to anyone who has studied physics,
expresses the linear relation between the current flowing in a conductor
and the voltage applied to it- the ratio of the voltage to the current being
called the resistance. Alternatively, the linearity can also be expressed
in terms of the conductance-the ratio of the current to the voltage. So familiar
is the law that it seems almost common sense, yet in many ways it is very
subtle indeed. We know that the electrical current is due to the flow of
electrons and the voltage is due to the presence of an electric field. It
follows that a steady current is a steady flow of electrons. However, the
definition of an electric field means that it exerts a force on any charged
particle such as an electron, so Newton's laws of motion would predict that
the electrons would accelerate. How then is it possible for a steady current
to flow?
The answer to this question was supplied by another German
physicist, Paul Drude, in the early years of the century. The picture he
introduced was of an electron being accelerated by the applied electric field
and then undergoing a collision which "scrambles" its motion before it is
accelerated again to another collision and so on. The net result is that
the electrons acquire, on average, a drift velocity of a few millimetres
per second superimposed on their much higher speed of random motion of a
few hundred kilometres per second. It is the average drift which is the current,
so the resistivity of a material depends principally on the number of electrons
free to move and how far they call go on average before undergoing a collision
which alters their momentum. This distance is called the elastic mean free
path and it is a measure of the quality of a conductor. In a typical metal
say copper at room temperature, it is only 30 nanometres. An electron will
undergo many millions of collisions while travelling the length of an ordinary
piece of wire.
Making electrons move in mysterious ways |
||||
| MOLECULAR beam epitaxy is the growth of layers of material
by firing beams of atoms or molecules at a suitable substrate.The process
takes place in an ultra high vacuum to remove impurities and collisions with
air molecules. Amazingly, provided the substrate temperature is carefully
controlled, the molecules stick to the surface but remain sufficiently mobile
to form very high- quality crystalline layers. It is, therefore, possible
to grow crystals atom by atom (typical rates are around 1 micrometre per
hour) with complete control of composition.
Two compound semiconductors, gallium arsenide (GaAs) and aluminium
arsenide (AlAs),are particularly attractive for this sort of layered growth.
Not only do they have the same crystal lattice structure, but the spacing
between atoms in both structures is also almost identical. Successive layers
of each; or intermediate alloys (AlGa)As; can be grown in a
heterostructure,introducing the minimum of atomic misalignment.
An electron moving in a semiconductor has a minimum kinetic
energy; known as the conduction band minimum. In (AlGa)As this minimum is
higher than in GaAs. The conduction band minimum can be thought of as the
potential energy of an electron in a given layer. However, the situation
is usually more complicated in a heterostructure because an individual electron
feels the electrostatic effect of all the other electrons, plus the positive
charge due to impurity atoms ("dopants") which have been introduced to increase
the electron density.
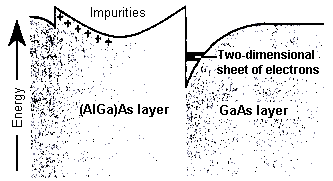
Because of the different conduction band minima, electrons
are confined within a plane in the GaAs layer, very,close to its junction
with the (AlGa)As layer. They sit in the area of lowest potential energy;
called the triangular region (left). The spatial extent of the region is
tiny-comparable with the wavelength of the electrons, which consequently
form a standing wave. All the mobile electrons in the heterostructure have
this standing wave character but are free to move in the other two directions.
Such electrons are called a two-dimensional electron gas or 2DEG. Their motion
is confined quantum mechanically to a plane perpendicular to the growth direction
of the heterostructure.
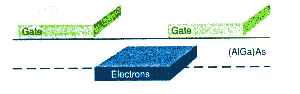
Further confinement of the electrons can be introduced by
evaporating thin metallic strips, or "gates", to the top surface of the
heterostructure. A negative voltage applied to the gate raises the potential
energy of the electrons locally beneath the gate. Sufficient voltage can
raise the potential energy enough to reduce the electron concentration to
zero. However, if there is a gap in the metal strip forming the gate, then
immediately beneath the gap there will still be some electrons. These split
gates, first developed by Mike Pepper's group at the University of Cambridge,
enable the creation of narrow conducting channels in the 2DEG between the
gates. If the channel is made narrow enough, standing waves may be set up
across the width of the channel to force the electrons into one-dimensional
motion along the wire. |
Drude's theory treated the electrons as if they were classical
particles, simply obeying Newton's laws. But we now know that classical mechanics
is usually insufficient to describe electrons. For example, it is completely
impossible to understand the physics of electrons in atom without invoking
quantum mechanics, in which the electron is considered to be a wave analogous
to light or water waves. The important parameter here is the wavelength of
the electron wave, which depends on its energy. In a typical metal this is
only a few times larger than the spacing of atoms in the crystal and is much
smaller than the electron mean free path. In such situations, where the electron
wavelength is very small compared to other lengths in the system, the classical
description of the electron motion is a good approximation. This is why Drude's
theory worked so well.
To see quantum effects, or for the
classical approximation to break down, it is necessary to do two things.
First, the size of a device must be made small enough to he comparable to
the electron wavelength. Secondly the material must be made pure enough to
remove the effect of collisions. The first condition is almost impossible
to achieve in a metal where the electron wavelength is very small,but it
is far more plausible in a semiconductor in which the electrons may have
much smaller momentum. Since the electron wavelength depends inversely on
momentum, the wavelength may he considerably larger than in a metal. With
modern technology it is possible to produce devices which are smaller than
the elastic mean free path and comparable with the electron wavelength.
But the second condition - to remove the effect of collisions
- must also be met. To see how this can be done, it is necessary to
consider what causes the collisions in the first place. Collisions are caused
by imperfections in the periodicity of the crystal. These can be due either
to vibrations of the atoms, just like masses on springs, or to permanent
imperfections such as dislocations or impurities. It is relatively easy to
remove the vibrations by lowering the temperature. To remove the impurities
and dislocations requires both high-quality crystal growth and very pure
material.
One of the best ways to achieve these dual goals is to grow
a very pure crystal with alternate layers of two semiconductors. This so-called
semiconducting heterostructure (see Box) is
made using molecular beam epitaxy (see "A quantum leap to smaller chips",
New Scientist, 12 January 1991). The epitaxial growth technique creates
almost perfect crystals by the deposition of atoms one at a time. Paradoxically
it is necessary to add impurity atoms to the heterostructure to provide the
electrons. [So worshipping "pure crystals" negates the fact that physically
impurities sometimes need to be introduced to obtain an effect -LB]
Without them, the material would not be able to conduct
electricity. But the impurity atoms are physically separated from the electrons,
and the probability of the two colliding is much reduced. Mean free paths
of a tenth of a millimetre are possible, thousands of times longer than in
copper at room temperature. So if the device is smaller than this, the electrons
can move ballistically, that is, in straight lines without collisions, and
an electrical signal may be transmitted much more quickly.
Another feature of the electrons in a heterostructure is that
they move strictly in a plane (see Box) and
for this reason the electrons are said to form a two-dimensional electron
gas or 2DEG. This allows the energy of a ballistic electron to be conserved,
because in a 2DEG the frictional process that is equivalent to air resistance
for a projectile in air is negligible.Hörst Stormer and his colleagues
at AT&T Bell Laboratories, New Jersey, have used this property to develop
a ballistic switch.
Just like light
If an electron passes through a region where its potential energy is increased,
then its kinetic energy will be reduced and it will slow down. It is relatively
easy to introduce regions of higher potential energy electrostatically by
applying voltages to metallic layers, or "gates", fabricated on the surface
of the heterostructure in which the 2DEG is embedded. The slowing of the
electron under one of these gates is analogous to the slowing of a ray of
light as it passes into glass. The electron trajectories are equivalent to
the rays in ray optics, and by suitable choices of the shape of the gates,
electron prisms and lenses can be constructed-as Stormer and his colleagues
have shown. Of course, it is very easy to change the "refractive index" in
this system because the speed of the electron depends on the magnitude of
the electrostatic potential. Such prisms and lenses have been used in the
laboratory to deflect electron beams, creating very fast switches. The major
drawback to commercialisation is that they require very low operating
temperatures-around one degree above absolute zero.
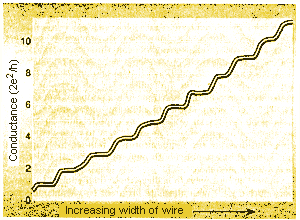 |
| When electrons move ballistically in a wire, the resistance is not zero. Instead, the conductance increases in a stepwise way as the width of the wire increases. Each step corresponds to an increase in the number of one-dimensional conduction channels in the wire. |
To a physicist, such ballistic switching devices are an excellent
example of how we can use Newton's laws to describe the motion of the electrons.
But they also lead to the question: "What is the resistance of a wire in
which the electrons undergo no collisions?" Bearing in mind Drude's model,
many scientists believed that the resistance would be zero. They turned out
to be wrong - for reasons intimately related to the quantum mechanical character
of the electrons. The unravelling of the unexpected results has led to a
new way of thinking about the conduction of electricity in small devices.
In the mid-1980s, Mike Pepper and his group at the University
of Cambridge pioneered fabrication techniques which could be used to form
just about any shape of conductor from a 2DEG, including narrow wires. Both
the length and width of the wire are much shorter than the mean free path.
In 1988, such devices were first studied simultaneously at Cambridge and
also in the Netherlands in a collaboration between Delft University of Technology
and Philips Research. Far from having zero resistance, or equivalently infinite
conductance, the conductance of the wire jumped from one constant value to
another as the width of the wire was increased (see
Figure).
This was surprising enough, but the values of the conductance
on these plateaus were all equal to an integer multiplied by a constant.
That constant was precisely equal to 2e2/h where e is the charge
of the electron and h is Planck's constant. This was a staggering result.
It meant that the resistance of a wire in which the electrons had no collisions
was not zero but took on discrete ("quantised") values which depended only
on fundamental constants of nature and was independent of the length of the
wire and the material from which it was made. Such wires became known as
quantum point contacts (QPC).
Quantised conductance is best understood by using ideas developed
in the mid-1980s at IBM's Thomas J. Watson Research Center at Yorktown Heights
in New York state, by Joe Imry, Rolf Landauer and, most notably, Marcus Buttiker.
The central concept is one familiar to quantum mechanics-that the measurement
perturbs the system. Although the wire itself contains nothing that impedes
the electrons, any external apparatus such as an ammeter, current source
or voltmeter, must be connected to the wire via electrical contacts which
do contain lots of defects and impurities with which the electrons can collide.
These contacts act as "reservoirs" which will accept electrons impinging
upon them and, also, will inject electrons into the wire. So the idea is
that the wire itself really does have little or no resistance but that as
soon as any electrical leads are attached, as is always necessary in a
measurement, collisions are introduced and a non-zero resistance is measured.
This explains why the resistance is non-zero and also why the resistance
is independent of the length of the wire.
But it does not explain why the resistance takes on discrete
values. This is a direct consequence of the quantum mechanical character
of the electrons. With wires of such small dimensions, comparable with
the electron wavelength, the electron motion is strictly one-dimensional,
with electrons forming standing waves across the width of the channel
(see Box). By increasing the width of the wire,
several one- dimensional (1D) states will result, each corresponding to a
particular standing-wave in the channel. These 1D states can be considered
as independent provided that there is no possibility of an electron transferring
from one state to another along the length of the wire-which will be the
case if the electrons are travelling ballistically. In each 1D state, the
ability to carry current, or the conductance, depends on the number of electrons
and how fast they are travelling.
Generally both the number of electrons and their speed depend
on the material through which the electrons are travelling. But in 1D, and
only in 1D, the properties of the material cancel out when the number and
the speed are multiplied together. So the conductance of a 1D state depends
only on fundamental constants. The conductance of the wire will then be the
conductance of a 1D state multiplied by the number of 1D states in the wire.
This number is determined by the number of electron half-wavelengths that
can be fitted in the width of the wire. Therefore, the conductance of the
wire depends on its width and not on any property of the material.
The potential application of QPCs to digital electronics is
this: in principle, simply by applying a known voltage to a gate, one would
be able to regulate the resistance of the device between rigidly defined
quantised values, to act as a logic element in a computer or a voltage-controlled
resistor. There are, unfortunately some very serious problems, most notably
the stability of the devices, and the requirement for temperatures near to
absolute zero. This seems to be fundamental, so it is highly unlikely we
shall ever see a commercial device based on a QPC even in a very specialised
electronic application.
Single electrons
In the devices described above, and indeed in Drude's basic theory, the electrons
are treated successfully as independent, non-interacting particles. At first
sight, this is most surprising because, in a vacuum, electrostatic forces
due to the electron charge mean that electrons strongly repel each other.
However, a solid is made from neutral atoms, and for each negatively charged
electron there is a positively charged ion. The positively charged ions
compensate most of the effect of the electron charge. This screening allows
electrostatic forces between electrons to be largely ignored in a normal
solid. However, the new microfabrication technology has enabled construction
of a new class of device in which these forces cannot be ignored.
These microscopic devices, made from metals or semiconductors,
were pioneered in the late 1980s by Hans Mooij's group in Delft University
of Technology, Michel Devoret in Saclay France, and others. They have a very
small capacitance (c) and are sensitive to the presence of a single electron.
Capacitance is the ability of a system to store electrical charge. Mooij's
capacitors have a capacitance so small that the addition of a single electron
causes an appreciable rise in the voltage across the device. The single-electron
transistor is a charge- sensitive device which can detect the presence of
an excess charge equivalent to that of one electron.

Another similar and equally fascinating structure is the "electron
turnstile". This relies on the fact that the electron possesses a discrete
charge (e), so that any movement of charge through a circuit involves at
least this amount of charge. If an electron is to pass between the plates
of a microscopic capacitor, the energy provided by the voltage difference
across the capacitor must exceed the minimum charging energy
(e2/2c). (The charging energy is inversely proportional to the
capacitance, so it is negligible in the larger capacitors found, for example,
in a transistor radio.) By adjusting the voltage drop across the microscopic
capacitor it is possible to control the passage of electrons one at a time.
Konstantin Likharev at the Massachusetts Institute of Technology has suggested
that this might be the basis for electronics in which a "bit" of information
might be carried by a single electron-the ultimate in digital technology.
The electron turnstile has another application that is interesting
at the most fundamental level. By applying a gate voltage that is oscillatory,
the current (I) through the turnstile is given by the charge on the electron
(e) multiplied by the frequency at which the voltage (V) is altered. Since
the application of a voltage step to the gate allows one electron through
the device, an alternating voltage will allow a steady flow of electrons,
one by one, and hence an electrical current. The current through the turnstile
is then just the charge on the electron multiplied by the frequency with
which the gate voltage is altered. Currents are very small-a frequency of
10 MHz only gives a current of 1.6 picoamperes-but scientists involved with
measuring fundamental constants, including Tony Hartland at the National
Physical Laboratory, Middlesex, are excited that this might enable an independent
current standard where the ampere is defined in terms of fundamental constants
of nature. As well as being useful in its own right, such a device might
also resolve a puzzling anomaly in the determinations of the ratio
e2/h, where e2 is the square of the charge on the electron,
and h is Planck's constant. High-precision calculations of the fine structure
constant, which is proportional to e2/h and relates to the differing
energy states of the atom, yield one result, while measurement of quantised
conductance in the quantum Hall effect, analogous to that seen in a QPC,
yields another. The two values disagree by a margin much greater than the
experimental errors in their measurement.
The development of ultra-small capacitance circuits as well
as the other ballistic and quantum devices has stretched existing theories
of electrical conduction beyond their limits. Scientists can routinely fabricate
structures which rely for their operation on the quantum character of the
electrons or the fixed charge. As yet, manufacturers show little or no interest.
To break that barrier, physicists will need to find a way to make these devices
work at about room temperature and, just as important, with a degree of
reliability that has not been achieved to date.
On a more fundamental level, it is likely that the physics
will continue to be driven by technology. As fabrication techniques improve
until perhaps one can control small groups of atoms, or even single atoms,
then the distinction between physical manipulation and chemical reaction
will be blurred. There is the prospect of a truly molecular electronics.