

by Ian Stewart
Arithmetic and Old Lace
Who is a mathematician? Some years ago, in a rare flash of insight, it dawned on me that a mathematician is somebody who sees an opportunity for doing mathematics where others might not. Consider shoelaces. The potential for extracting significant mathematics from shoelaces is not widely recognized. That it exists was made clear to me by the article "The Shoelace Problem," by John H. Halton, who is in the computer science department of the University of North Carolina at Chapel Hill. It appeared in the Fall 1995 issue of the Mathematical Intelligencer.
There are at least three common ways to lace shoes [see illustration below]:
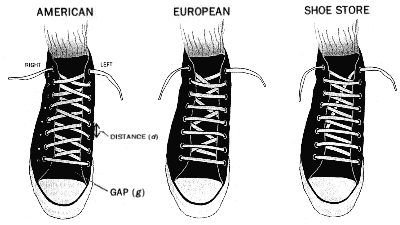 |
| LACING PATTERNS on a sneaker can have different complexities and lengths. Which of these patterns requires the least lace? |
American zigzag, European straight (from which the term "straitlaced" is derived, though perhaps by way of garments rather than shoes) and quick-action shoe store. To the purchaser; styles of lacing can differ in their aesthetic appeal and in the time required to tie them. To the shoe manufacturer; a more pertinent concern is which type of lacing requires the shortest-and therefore cheapest-laces. In this month's column I shall ask the shoe manufacturer's question.
To find the amount of lace, I will focus only on the length represented by straight line segments. The amount of extra lace required to tie an effective bow is the same for all methods of lacing, so it can be ignored.
My terminology will refer to the lacing as seen by the wearer, so that the "top" row of eyelets in the figure lies near the ankle. I will also idealize the lace to be a mathematical line of zero thickness and the eyelets to be points. Using a brute-force attack, one can then calculate the length of the lace in terms of three parameters:
· The number n of pairs of eyelets
· The distance d between successive eyelets
· The gap g between corresponding left and right eyelets
With the aid of Pythagoras's theorem (one wonders what the great man would have made of this particular application), it is not too hard to show that the lengths for the lacings are as follows:
· American: g +2(n - 1)Ö(d2 + g2)
· European: (n - 1)g + 2Ö(d2 + g2) + (n - 2)Ö(4d2 + g2)
· Shoe store: (n -1)g + (n -1) x Ö(d2 + g2) + Ö((n -1)2 d2 + g2)
Which is the smallest? Suppose, for the sake of argument, that n = 8, as in the figure, d = 1 and g = 2. Then the lengths are:
· American: 2 + 14Ö5 = 33.305
· European: 14 + 2Ö5 + 6Ö8 = 35.443
· Shoe store: 14 + 7Ö5 + Ö53 = 36.933
But can we be certain that American is always the shortest? Some careful high school algebra shows that if d and g are nonzero and n is at least 4, then the shortest lacing is always American, followed by European, followed by shoe store. If n = 3, American is still shortest, but European and shoe-store lacings are of equal length. If n = 2, then all three lacings are equally long, but only a mathematician would worry about such cases!
Still, this algebraic approach is complicated and offers little insight into
what makes different lacings more or less efficient. Halton instead observes
that a clever geometric trick makes it completely obvious that American lacing
is the shortest of the three. The idea owes its inspiration to optics, the
study of paths traced by rays of light.
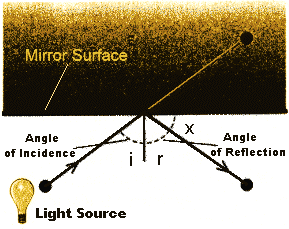 |
| FERMAT'S PRINCIPLE for deriving the path of a light ray reveals that the angle of reflection equals the angle of incidence. |
Mathematicians discovered long ago that the geometry of light rays can be made more transparent (so to speak) by applying carefully chosen reflections to straighten out a bent light path. For example, to derive the classical law of reflection-"angle of incidence equals angle of reflection "Consider a light ray that hits a mirror and bounces off. If you reflect the second half of the path about the plane of the mirror [see illustration at top left], the result is a path that passes through the mirror and enters Alice's world behind the looking glass.
According to the principle of least time, a general property of light rays enunciated by Pierre de Fermat, such a path must reach its destination in the shortest time-which in this case implies that it is a straight line. Draw a line perpendicular to the mirror at the point of incidence. Then the angle marked m in the figure is equal to the angle of incidence i; further, the two angles marked x are equal. But ni + x = 90°, and if r is the angle of reflection, r + x = 90° as well. So m = r = i.
Halton derives geometric representations of all three types of lacing by
an extension of this reflection trick. He draws a diagram [see illustration
at bottom right] made of 2n columns of eyelets spaced distance
d apart in the vertical direction. Successive rows are spaced distance
g apart horizontally. (To shrink the diagram, we have reduced
g; the method works for any values of d and g.) The
last column of the diagram represents the left-hand column of eyelets; the
second-last column represents the right-hand column of eyelets. Overall the
odd-numbered columns represent left-hand eyelets, and even-numbered columns
represent right-hand eyelets.
| REFLECTION TRICK (left) allows the shortest lacing to be derived geometrically. Instead of zigzagging, the lacing path is reflected at each eyelet, so that it is straightened out as much as possible. American lacing becomes the straightest, because it runs along one side, rather than two, of each small triangle (gray). It is therefore the shortest. |
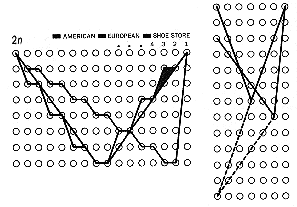 |
| COMMON SEGMENTS (right) are eliminated in order to compare the shoe-store and European lacings. The shrunken paths,when reflected about a horizontal axis, finally show that shoe-store lacing is the longest. |
The polygonal paths that zigzag across this diagram correspond to the lacings, but with an extra "twist." Start at the top left-hand eyelet of a lacing pattern and draw the first segment of lace, running from left to right of the shoe, between columns 1 and 2 of the diagram. Draw the next segment of lace between columns 2 and 3 instead of going back from column 2 to column 1 as for a real shoe. In effect, the segment is reflected as though the columns of eyelets were replaced by mirrors. Continue in this manner, reflecting the position of each successive segment whenever it encounters an eyelet. Instead of zigzagging between the two columns of eyelets, the path now moves steadily to the left of the figure.
Because reflection of a segment does not alter its length, this representation leads to a path that has exactly the same length as the corresponding lacing pattern. The added advantage, however, is that it is now easy to compare the American and European patterns. In a few places they coincide, but everywhere else the American pattern runs along one edge of a thin triangle, whereas the European one runs along the other two edges. Because any two sides of a triangle exceed the third side in length (that is, a straight line is the shortest path between two given points), the American lacing is clearly shorter.
It is not quite so obvious that the shoe-store lacing is longer than the European. The simplest way to see this is to eliminate from both paths all horizontal segments (each path has n - 1 horizontal segments, which contribute the same amount to both lengths) and also the two sloping segments that match up. The elimination results in two V-shaped paths; shift the truncated European path so that it again shares the first eyelet with the shoe-store path. If each V is now straightened out by reflection about a horizontal axis placed at the tip, it finally becomes easy to see that the shoe-store path is longer, again because two sides of a triangle exceed the third side.
These cunning reflection tricks can do more than compare particular lacing patterns. Halton uses them to demonstrate that the American zigzag lacing is the shortest among all possible lacings. More generally, shoelaces and Fermat style optics become united in the mathematical theory of geodesics, the shortest paths in various geometries. There, mirror reflections answer fundamental questions in physics, as well as confirming the superiority of the American way of lacing shoes.
Tom Sales of Somerset, N.J., sent me a fascinating letter inspired
by the February column on zero knowledge protocol - means of proving that
you know the rules without revealing them. Years ago in this Journal,
Martin Gardner introduced a card game called Eleusis,
in which one player invented rules and the others had to guess them by being
told whether a given play was legal or illegal. At that time, Sales invented
a similar game, involving a mouse, Alpha, that inhabits a triangular room.
|
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |