

by Ian Stewart
The Rise and Fall of the Lunar M-pire
While rummaging through a storeroom in the Louvre last fall, curator
Jean-Jacques Le Maire discovered a carton containing some unpublished papers
of Jules Verne. Unfortunately, a mouse had nibbled through the papers many
years before. Le Maire and his colleagues are desperately trying to piece
the material back together.So far they have restored a previously unknown
chapter from Verne's 1865 classic Round the Moon. Le Maire has kindly agreed
to publish the material in Scientific American.
Major Elphinstone paced back and forth inside the dome of Baltimore observatory
as his associate J.T. Maston peered Through the eyepiece of the observatory's
main telescope. "I don't see them yet," Maston said nervously.
"May I look?" Elphinstone asked. "Of course," Maston replied, picking up
a large notebook of mathematical calculations. "If the quantity of guncotton
had been misjudged by a mere 1 percent," he said, "then there could be a
delay of several hours. I believe we should not yet conclude that some terrible
fate has befallen Barbicane, Nicholl and Ardan."
"Quite right," Elphinstone sighed. "One must think positively." The Major
shivered.
"It is devilishly cold out here on Long's Peak! I suggest we retire to the
main building for an hour and then return to the observatory to renew our
search."
"I am a little concerned lest any news come through on the ticker-tape machine."
They stared at the tiny machine that had been installed in a corner of the
dome. "Any news will be recorded on the tape, Maston. We can easily check
it when we return." Maston reluctantly agreed, and the two gentlemen walked
quickly to the warm lounge of the building. A servant was summoned to bring
them coffee and sandwiches. The Major noticed a map of
the world on the wall-German territory in orange, French in green, American
in purple and the British Empire in pink.
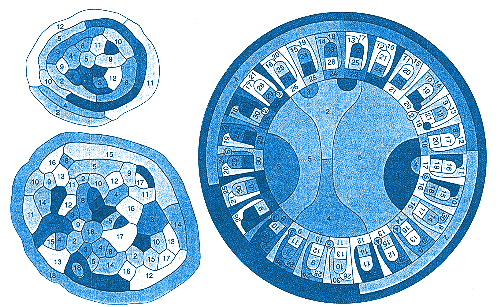 |
| CARTOGRAPHER'S NIGHTMARE : If one were to make a map of several empires, each of which consists of two countries,what would be the maximum number of colors needed to guarantee that no two adjacent countries would be the same color and that countries in the same empire would be the same color? The map at the top left requires 12 colours,and in fact, no map of empires of two countries ever needs more than 12.For empires consisting of three countries,the maximum number of colors needed is 18 (bottom left),and for empires of five countries,the total is 30 (right). |
"Soon we shall redraw that map," Elphinstone boasted. "Pardon?" "We will
adjoin a map of the moon, and it, too will be colored
purple. An American colony on the moon. The sun may never set on the British
Empire, but the American Lunar Colony will rise above every nation on the
earth."
"Ah," said Maston, who had little interest in building an empire. "There
might have to be some green, too."
"Excuse me?"
"On the map of the moon," he said apologetically.
"Don't forget that Ardan is French." Seeking to change the subject, he wandered
over to the map. "I wonder why cartographers use so many colors? There must
be at least a dozen."
"So?"
"I was told not long ago by a relative, a mathematician at Harvard, that
someone named Percival Heawood has proved that any map on the surface of
the globe can be colored with no more than five colors. The problem, if I
recall correctly, was first posed by the Englishman Francis Guthrie in 1852."
(Editor's note: In 1879 Arthur Kempe, a barrister
and a member of the London Mathematical Society, claimed a proof that
four colors would always suffice; however,
11 years later Heawood found a subtle error. For almost a century, nobody
knew whether every map can actually be four-colored. Finally, in 1976, with
substantial computer assistance, Kenneth Appel and Wolfgang Haken of the
University of Illinois proved that five colors are never needed.)
Elphinstone thought for a moment. "But surely one color will suffice?" "Hmm?
Oh. I failed to mention that adjacent countries must receive different colors."
"I see," the Major said. "What about 100 countries adjacent only at a common
point, like slices of a pie?"
"I should clarify my terms," Maston answered. "By 'adjacent' I mean that
they share some common boundary of nonzero length. Now, I notice this map
appears to use many more colors than is necessary. But I suppose criteria
other than mere adjacency were used."
Elphinstone finished his coffee and called for a brandy. Suddenly Maston
leaped to his feet in excitement. "I have just remembered an extension of
the map-coloring problem," he explained.
"Suppose that instead of countries, we consider empires. Countries belonging
to the same empire must receive the same color, of course. Different empires
may also receive the same color, however-subject to the same rule as before:
if two countries are adjacent, then they must receive different colors."
"Logical."
"Indeed. The implication, of course, is that if any two empires possess adjacent
territories anywhere on the globe, then those empires must receive different
colors. Let me say that an empire that contains exactly two countries- each
country being a single connected region-is a 2-pire; one that contain' three
countries is a 3-pire, and so on. Then an empire with m countries would be
called an m-pire. I must apologize for the feeble joke."
"Yes," the Major muttered. "You must. "In my defense, I should point out
that it is not mine, but Heawood's."
"I wonder if he realized that an empire with x countries would he called
an x-pire?"
"Good point," Maston conceded.
"Any way, in 1890 Heawood proved that one needs at most 12 hues to color
any given map consisting of 2-pires.
"Heawood discovered a map with 12 mutually adjacent 2-pires [see illustration
on opposite page], which perforce required distinct colors, thus proving
that 12 is the smallest possible number of colors in general. Heawood Went
further and proved that every map consisting of m- pires requires no more
than 6m colors."
"And did he show that this number is also the best possible?"
"No, he did not. But he conjectured such a result. In fact, he suggested
that there always exists a map with precisely 6m mutually adjacent m-pires."
(Editor's note: In 1984 Brad Jackson of San Jose State University and
Gerhard Ringel of the University of California at Santa Cruz proved Heawood's
conjecture. A map of 18 mutually adjacent 3- pires, discovered by Herbert
Taylor of the University of Southern California, is shown on the opposite
page as well as a map with 30 mutually adjacent 5-pires.)
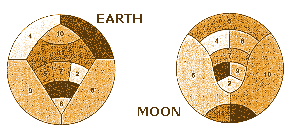 |
| MAPMAKER'S INCUBUS: What is the maximum number of colors needed for a map in which every empire consists of two countries, one on the earth and the other on the moon? Nine colors are sometimes needed, as shown above, but no one knows whether there are some such maps that require 10, 11 or even 12 colors. |
The Major ordered a second brandy.
"Would it make any difference if some of the countries in an m-pire were
on the moon?" he interjected. Maston thought for a moment. "Probably," he
said.
"After all, we are now considering maps on a pair of spheres instead of just
one. I suppose the simplest case would be when each country on the earth
is the possessor of a 2-pire, of which the second country is a lunar colony.
I believe methods akin to Heawood's will show that the maximum number of
colors required lies somewhere between eight and 12."
(Editor's note: Rolf Sulanke of Humboldt University in Berlin showed that
some such maps require nine colors, but it is still not known whether the
correct answer is 9, 10, 11 or 12. The reader might like to consider 3-pires,
each having one territory on the earth, the moon and Mars. For three planets,
the optimal number of colors is either 16, 17 or 19; form greater than or
equal to four, it is either 6m - 2, 6m - 1 or 6m.)
Elphinstone and Maston made their way back to the observatory. "Still no
word," Elphinstone reported, checking the ticker tape. Maston turned the
great handle that moved the telescope on its mountings. He bent down and
placed his eye against the instrument.
"Any luck?" Elphinstone asked.
"No, not yet." Maston fiddled with the settings.
"Ah! There she is!"
"May I look?" The Major could barely make out a tiny dot against the lunar
landscape.
"So they made it. Soon there will be a new map with a purple moon!" "And
a dash of green," Maston added.
"Yes, of course," Elphinstone said, taking another peek through the telescope.
"My word! I think I see several other spacecraft." The ticker-tape machine
suddenly began to chatter. Maston rushed over to read the message:
"INTERCONTINENTAL NEWS AGENCY REPORTS THAT MANNED MISSILES WERE LAUNCHED
TO THE MOON TODAY BY ARGENTINA, BELGIUM, BRAZIL, BRITAIN, CHINA, GERMANY,
HOLLAND, JAPAN, PORTUGAL, SPAIN, RUSSIA AND THE UNITED STATES." The Major
stared at Maston.
"I believe you were saying purple, green and between seven and 10 additional
colors?"
Further Reading PEARLS IN GRAPH THEORY: A COMPREHENSIVE INTRODUCTION. Nora Hartsfeld and Gerhard Ringel. Academic Press, 1990 |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
SCIENTIFIC AMERICAN April 1993 File Info: Created 18/6/2000 Updated 12/10/2005 Page Address: http://members.fortunecity.com/templarseries/mpire.html