Mathematical Recreations

by Ian Stewart

A Bundling Fool Beats the Wrap

Silas Golding was finishing his first day of work as a tennis-ball packer for the Sportsware Shipping Shop. "Billy Jo, could you pass me another seven cans?" he asked. "And while you're at it, how about some shrink-wrap film?
"Just let me wrap these basketballs," Billy Jo Rottweiler said. After cutting a piece of film, she handed him seven tennis-ball cans and the roll of film.
Silas covered his workbench with a long sheet of film, placed the cans on top, side by side, and then folded the sheet over, wrapping the cans as carefully as a parent diapers a baby. Then he put the entire package in a machine, which shrunk the film around the cans. The plastic fitted snugly around the edges of the bundle, but some spaces remained in the middle. Silas casually picked up the package, and its contents spilled onto the floor. The crash startled everyone in the shop.

"Golding'. You've done that a hundred times today," the supervisor yelled.
"Sorry, sir."
"Would you like to work here tomorrow, you uncoordinated sloth?"
"Yes, sir."

"Then I suggest you find a way to wrap the cans properly. Why not try binding them up in a more compact bundle?"

"But Billy Jo packs her basketballs in a line-like a string of sausages" Silas protested. "And she stretches the wrapping tightly just as I do, so that there aren't any dents or anything. That is, the packs are always convex in shape."

"Yeah, but my packs don't fall apart," Billy Jo interjected.

"So, why doesn't it work with cylindrical cans?"the supervisor asked.

"Well, sir," Billy Jo continued, "I can see that if the total volume of the pack-including any air spaces-is as small as possible, then the pack won't collapse. Because if it did, you could shrink it even further, and you can't, so to speak. So we've got to think about packs whose volume-including every-thing inside the wrapper, air and all-is as small as possible but is still convex."

"I can see that the surface area of the bundle is a lot bigger when the cans are arranged in a line," the supervisor said. "Of course, that's determined by

how long the strip of wrapping film must be. But I'm not so sure about the volume."

"Suppose," said Billy Jo, "the cans have a radius of length l,to keep the calculation simple. If you look down on the top, then in essence you're just packing a lot of circles together and wrapping an elastic band round them. The volume of your pack is proportion-alto the area inside the band; the surface area of your wrapping is proportional to the length of the band, assuming you don't cover the ends when you wrap the cans up."

"Right."

"So we can find the area inside the band and the length of the band. It's a lot easier to think in two dimensions. Now, if you put seven circles in a line and wrap a band round to get a tight fit with convex edges, the total perimeter is 2p + 24 = 30.283."

"Why?"
"Each straight side has length 12-six diameters of the circles-and then there are two semicircles, each of length p."

"Okay."

"But if you arrange six circles in a hexagon and place one in the center, the perimeter becomes 12 + 2p = 18.283. It's a similar argument: there are six straight sides whose lengths are equal to a diameter and six arcs, each mal:ing up one sixth of a circle."

"I can see that, Rottweiler."

"So the perimeter for the hexagonal arrangement is only a bit more than half the length of the sausage. that's why Silas's packs keep collapsing: if the cans are moved a little bit, the wrapping gets loose."

"But all you've done is calculate the perimeter, Rottweiler. What about the volumes?"

"I should be able to use the same kind of method, sir. If you arrange the cans in a sausage, the total area inside the bundle can be split up as six squares with sides of length 2 plus two semicircles with radii of length 1; so that's 24 + p = 27.141. On the other hand, if you arrange the cans in a hexagonal group, it's kind of tricky to work out the volume. There are lots of funny bits with curved edges."

"Isn't there a formula for things like that, Rottweiler?"

"Not in any textbooks I know of. I'll have to figure it out." She grabbed a pencil and some scrap paper. "Hmm.

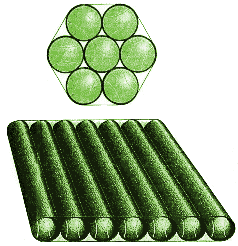SEVEN CYLINDERS can be wrapped together in a bundle or a row. Which of these packages has the smaller volume, and which  is less likely to fall apart?

Seems to me I've got to work out the areas of two kinds of shape-apart from circles. There are 'center holes,' with three curved sides, and 'edge holes,' with two curved sides and one straight [see illustration at right]. A central hole is really an equilateral triangle minus three 60-degree sectors of a circle. The equilateral triangle has sides of length 2; therefore, its height is Ö3, and its area is half the base times the height, which is (¹/₂) x 2 x Ö3 = Ö3. The three sectors together form a semicircle of area ^p/₂. So a central hole has an area Ö3 - ^p/₂= 0.161. Similarly, two edge holes plus two semicircles make a 2 by 2 square with area 4. Consequently, one edge hole plus one semicircle has an area half that, namely, 2. So an edge hole has an area

2 -^p/₂ = 0.429.

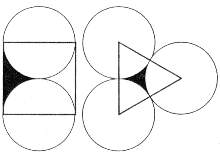THREE CIRCLES packed one next to the other leave a space that is equal to the area of the triangle minus half the area of one of the circles. On the other hand, the space between two circles and an edge is half the area of the square minus half the area of one of the circles.

Finally, a hexagonal bundle of seven circles has an area made up from seven circles, six central holes and six edge holes. That comes to

7p+ 6(Ö3 - ^p/₂) + 6(2 - ^p/₂) = 25.533.

Which is smaller than 27.141. See? That's why Silas's sausages collapse. He should make hexagons instead."

Fine," Silas said. "But I don't see why it doesn't work the same way with spheres. Surely if you pack your basketballs into a tight group, the total volume, wrapping and all, will be smaller than if they're arranged in a line."

"Not necessarily. It's a complicated problem, and it's genuinely three-dimensional. I don't see how to arrange seven spheres in a tight group without there being an awful lot of wasted space inside the wrapper. For my arrangement-that is, with all the balls in a line-the area of the wrapper is 28p, and the volume inside it is ^40p/₃ But it's not so easy to work out the math for other arrangements. Still, my packs don't fall apart. So that's experimental evidence I'm right."

"That is all very well," the supervisor declared, "but you often have to tie bundles with a lot more than seven cans in them. What shape will those have to be to minimise the volume inside the packaging, Golding?"

"Sort of-like the hexagon, sir, but bigger," Silas said.

"Like the hexagon, sir, but bigger," the supervisor whined, mimicking Silas. "You call that a good answer, Golding?"

"No, sir."

"And as for you, Rottweiler, you don't seem to have a handle on the spheres problem. You can calculate the volume only for the sausage shape,and then you assume it has the smallest volume."

She hung her head apologetically. "I want you both to spend some time in the company library, digging up any useful information you can. I'm sure somebody must have studied the problem before. No point in reinventing the wheel, is there?"

"Yes, sir," Billy Jo and Silas chimed in unison. "We mean, no, sir."

The next morning the supervisor found Billy Jo and Silas asleep in the library, their heads resting on open books. "Good morning. Find anything, you two?"

"Yes, sir. Quite a lot, actually, sir," Billy Jo said, waking abruptly.

"Well, then."

"Sir, the basic problem is to find arrangements of n-dimensional spheres in n dimensional space that minimize the n-dimensional 'volume' of their convex hull. Er, the convex hull is the smallest convex surface that contains all the spheres. In two dimensions, we're packing circles in the plane and trying to minimize the area of the convex hull; that's like packing Silas's cylindrical cans. In three dimensions, we're packing spheres, like my basketballs, and trying to minimize the volume."

"Go on."

"In two dimensions, the best arrangements are known to be 'as hexagonal as possible.'"

"I thought you'd found a precise answer, Rottweiler."

"Uh, well, sir, it's a bit tricky. I have to explain about Groemer packings. They're honeycomblike packings that form hexagons-not necessarily regular hexagons, but the sides have to be parallel in pairs. Oh, and some 'sides' may not occur at all-I mean, you could have pentagons and triangles and things like that [see bottom illustration].

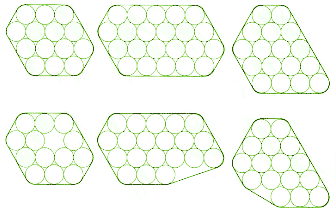GROEMER PACKINGS (top row) enclose the circles in the smallest possible area. The bundles in the bottom row are not Groemer packings,and in each of those cases,the circles can be packed into a smaller region.

They're named after Helmut Groemer of Oregon State University, who proved a fundamental theorem about them in 1960. It relates the area inside the convex hull of a circle-packing to the number of circles inside it and its perimeter. Namely, for n circles and perimeter p, the total area of the convex hull is at least

2Ö3(n -1) + p(1-^Ö3/₂)+ p(Ö3 -1).

Moreover, the area is equal to this expression if and only if the packing is a Groemer packing."

"And?"

"Starting from this estimate, Gerd Wegner of Dortmund University pretty much solved the entire problem in 1986. He showed that the convex hull of a set of n equal circles is minimal when they are arranged in a Groemer packing whose sides are as close to being equal as possible-at least provided n is less than or equal to 120. The theorem is also true if n is a 'hexagonal number' of the form 3k² + 3k + 1, when there is a Groemer packing forming a perfect regular hexagon."

"But there are still some unsolved cases?"

"Yes, but then the gap between the best-known results and the best that possibly could be achieved is very small."

The supervisor shook his head. "Not as precise as I had hoped, Rottweiler."

"No, sir," Golding said, leaping to her assistance. "But we never have to wrap more than 120 cans in one pack."

"True, but irrelevant to the theoretical problem," the supervisor replied.

"The strange thing is that in three dimensions, the answer is quite different-at least, for a smallish number of balls."

"A smallish number? " the supervisor asked quizzically.

"Anything up to and including 56, sir," Billy Jo added hastily. "For that many spheres, the arrangement whose convex hull has the smallest volume is a sausage-all the balls in a straight line. After that, though, the minimal arrangements get much more compact and rotund."

"Rotund, you say?"

"Less intuitive still is what happens in spaces of four or more dimensions," Rottweiler explained, ignoring her boss's banter.

"I don't think we make four-dimensional sports gear," the supervisor quipped.

"In any case, sir, as you just said, it's the theoretical point that matters."

"True. But what do you mean by four-dimensional space?"

"Well, two-dimensional space can be defined using two numbers as coordinates, (x,y), and three-dimensional space is every set of three numbers (x,y, z). Clearly, four-dimensional space is every set of four numbers (w,x,y, z), and n-dimensional space is every set of n numbers (x₁ ,.....x_n). That's it, really."

"And a sphere in n dimensions?"

"That's the set of points that lie within a distance of, say, one unit from a chosen point, the center. And of course you have to define the n-dimensional analogue of volume, but that's not too hard."

"I see."

"Anyway, for four dimensions, the arrangement of four-dimensional spheres whose convex hull has the least volume is a sausage for any number of balls up to about 50,000. It's not a sausage for 100,000 balls. So the best packing involves very long, thin strings of balls until you get an awful lot of them."

"How many exactly?"

"Somewhere between 50,000 and 100,000, sir. Nobody knows the precise value at which sausages cease to be the best. But the really fascinating change comes at five dimensions. At least, that's the conjecture. You might imagine that in five dimensions sausages are best for, say, up to 50 billion balls, but then something more rotund has a convex hull of smaller volume; for six dimensions, the same kind of thing holds up to 29 zillion balls, and so on. But in 1975 Laszlo Fejes Tóth formulated what is now called the sausage conjecture. It states that for five or more dimensions, the arrangement of balls whose convex hull has minimal volume is always a sausage, however large the number of balls may be."

"Good heavens," the supervisor exclaimed, genuinely surprised.

"What's so special about five dimensions?" Silas asked.

"Do bear in mind it's only a conjecture," Billy Jo pointed out. "But the heuristic evidence is quite strong. The basic idea is that as the number of space dimensions increases, it gets harder and harder to fill space efficiently with spheres. The gaps are multidimensional and become quite big. If you make the wrapping poke out along too many dimensions of the space, you leave a lot of gaps, which makes the volume quite large. Whereas if you confine the spheres to a single direction, in a sausage, you cut down the wasted volume so much that it all works. Tóth estimated the dimension at which the numbers for this argument work out, and the breaking point seems to be dimension five.

"It could all be rubbish, of course-nobody knows for certain. But it sure would be interesting to find out."

The supervisor tried hard not to look impressed. "Very well, you two," he said. "Good work. But now-back to your workbenches. You've got a lot of packs to wrap."

Silas spent the next hour wrapping 56 basketballs in a single sheet of plastic film. He Was so proud of his accomplishment that he called over the supervisor to take a look.

"Pretty amazing," the supervisor cheered.

Silas carefully lifted the package over his head in triumph, but the package bent and broke from its own weight. Fifty-six basketballs bounced around the room.

MAIN INDEX
REFERENCE GUIDE			TRANSCRIPTS				GLOSSARY
Chaos	Quantum	Logic	Cosmos	Conscious	Belief	Elect.	Art	Chem.	Maths