Almost 100 years ago Henri Poincaré encapsulated the way we think about space in a famous mathematical conjecture, but proving it has beaten the best minds. Until now. Bruce Schechter looks at a possible proof that has the world of mathematics on tenterhooks
WHEN the brilliant French mathematician Henri
Poincaré was not actually doing maths, he liked to think about the
nature of mathematical creativity. Logic, he felt,
was important, but it was not enough. "It is by logic we prove, Poincaré
wrote, "it is by intuition that we invent."
The problem, as Poincaré would have acknowledged, is that there is
a disconnect between intuition and logic. Mathematicians often have intuitions,
which they call conjectures or hypotheses. Many of these are remarkably resistant
to logical proof. One of the most famous is the Poincaré conjecture.
His conjecture is concerned with topology, the study of shapes, spaces and
surfaces.
Think, for example, of the way a noose looped round the Earth might be tightened
and its circumference eventually reduced to zero as it slips off at the North
Pole. Try to accomplish the same trick with a noose formed through the handle
of a coffee cup, and you'll find that there is a fundamental difference between
the Earth and a coffee cup. That is because they have different topologies.
Poincaré published his conjecture on the topology of
three-dimensional spheres in 1904 and it has been a driving obsession
for some mathematicians ever since. The obsession has now reached fever pitch
because it seems that it might finally have been proved. In 2003,
Grigori Perelman of the Steklov Institute of Mathematics in St Petersburg,
Russia, described calculations that appear to prove Poincaré 's
conjecture. A year on, the proof is holding. While nobody is ready to say
that his proof is completely free from logical flaws, the top minds in maths
have yet to find one. "The mathematics community will come to a consensus
soon, and I haven't heard an objection to the proof, so that tells you which
way I think it will go," says John Morgan of Columbia University in New York,
one of a group of eight top mathematicians checking the proof. "l am very,
very optimistic," he says.
 |
| Poincaré 's
topological conjecture has obsessed mathematicians for a century
|
If Perelman is vindicated, he will collect $1
million from the Clay Mathematics Institute in Cambridge, Massachusetts,
which has placed a bounty on seven unsolved mathematical problems. Yet the
money from Clay would be insignificant compared to the effect a proof would
have. This is because the Poincaré conjecture captures our most basic
intuitions about three-dimensional space. If the conjecture is not true,
then our intuitive understanding of spaces and shapes is mistaken.
So what is the Poincaré conjecture? It is concerned with a form known
as a 3-sphere. In an ordinary sphere - known as a 2-sphere -the surface consists
of all points the same distance from a single point in three-dimensional
space. A 3-sphere's surface is made up of all points the same distance from
a single point in four-dimensional space. Now imagine
a 3-sphere with a three-dimensional noose on its surface. Tighten the noose,
and it will shrink until the loop disappears. The Poincaré conjecture
says that the 3-sphere is the only finite three-dimensional space in which
every closed loop can be continuously shrunk to a point. To Poincaré
, it seemed intuitive (see "Making sense of the Poincaré conjecture",
page 28).
Bizarrely, the conjecture has been proved in higher dimensions. Stephen Smale
proved it for five or more dimensions, and in 1982 Michael Freedman proved
it for four. But the three-dimensional world that we live in turned out to
be the hardest to conquer, despite many brilliant attempts and a growing
understanding of three-dimensional surfaces set in four-dimensional space
-the so-called "3-manifolds".
| The Poincaré conjecture
is the hypothesis that any three-dimensional surface that doesn't have twists
or holes in it is the surface of a four-dimensional sphere It is easy to see that this is true for the two-dimensional surface of three-dimensional shapes |
MAKING SENSE OF THE POINCARÉ CONJECTURE
|
|
| A being living on a simply connected surface,
that is, one without holes or twists in it, tests whether he is living on
a sphere by casting a noose and drawing it tight
If the surface is not simply connected, the noose gets stock, so the surface must be that of a doughnut, or something even more complex |
 |
The Poincaré conjecture
says that the only three-dimensional surface , or manifold, on which a loop
can be shrunk continuously to a point is that of a four-dimensional sphere.
To Poincaré this seemed obvious, even though he would not prove it.
But most people find it tricky to visualise a sphere in four dimensions,
let alone loops on its surface. Poincaré came upon his conjecture by analogy with the two-dimensional surfaces of three dimensional shapes. Suppose you were an ant living on the two-dimensional surface of a three-dimensional shape. The topology of your world could be anything in three dimensions - a sphere, a doughnut. even a doughnut with a knot tied in it. But if you trace out a loop in your world and shrink it, you can only be sure it will shrink to a point if you live on the surface of a sphere (see Graphic, left). |
| Poincaré made
the leap from two dimensions to three. Beings, like us, seem to be trapped
in the three-dimensional "surfaces" of four-dimensional shapes. And in our
universe, it seems that we can shrink any loop we make down to a point if
the universe is finite the Poincaré conjecture would imply that we
are apparently lying on the surface of a sphere in four dimensions, rather
than any other shape. What would it be like to live on a three-dimensional surface that was not that of a sphere? If you were standing at the centre of a room in this type of world and had the magical ability to move freely through its walls, floor and ceiling, you would encounter similar weird effects experienced by our two-dimensional ant. Suppose you move up through the ceiling, say, you might re-emerge from the floor. In a similar way, walking through the font wall, you might emerge from the back wall. This would alert you to the fad that the room is actually a four-dimensional version of a doughnut, called a torus. Unlike the loop we cast on the surface of a sphere, a loop that goes off through the font wall of this room and re emerges through the back wall could not be shrunk to a point. |
||
Among mathematicians, the Poincaré conjecture has been considered
so unassailable that those who attempt to solve it are sometimes described
as suffering from "Poincaritis" - a term that smacks of hopeless obsession.
Poincaré himself had a bash at it, but quickly realised that his proof
was flawed. And so it has gone on for almost a century, with generation after
generation succumbing to Poincaritis. "I think of the Poincaré conjecture
as being a kind of treacherous block that people have crashed against," says
William Thurston, a mathematician at Cornell
University, New York, who is now, like Morgan, relentlessly checking Perelman's
work. "People have wasted a lot of time."
It was Thurston who carried out much of the groundwork for Perelman's work
in the late 1970s. Ever since Poincaré , mathematicians have discovered
more and more examples of 3-manifolds, equivalent to the different geometries:
dodecahedrons, cubes, toruses and soon. Although these manifolds all seem
to have different geometries, Thurston proposed that they were actually all
combinations of eight fundamental geometries, which he called the "primes".
Just as any number can be expressed as a product of
prime numbers, Thurston conjectured
that any manifold can be expressed as a combination of the eight prime
geometries. He called his hypothesis the geometrisation conjecture, and in
1982 he won the Fields medal,the mathematical equivalent of the Nobel prize,
for his work on it.
 |
| Grigori Perelman describes his thinking on a visit to Princeton University in 2003 |
One of these prime geometries is the sphere, so mathematicians immediately
realised that Thurston's work might provide a way into the Poincaré
conjecture. While the geometrisation conjecture seems to make things worse
at first glance, Thurston hoped it might be easier to prove than the
Poincaré conjecture because it was a more general pattern. It is often
the case that a difficult problem in mathematics is only solved after it
becomes clear that it is a specific instance of a more general principle.
In 1997, Andrew Wiles
of Princeton University finally proved Fermat's last theorem, which is the
statement that xn + yn = zn has no solutions
if n is greater than 2. But Wiles did not prove it directly. Instead he proved
a more general theorem, the Shimura-Taniyama-Weil conjecture, of which Fermat's
last theorem was a consequence.
So after Thurston's work, mathematicians turned their attention to solving
the geometrisation conjecture, hoping to bag the Poincaré conjecture
into the bargain. The next step came from Richard Hamilton, a mathematician
now also at Columbia who invented a technique known as the Ricci flow. The
Ricci flow is a powerful tool that uses the properties of a manifold to
investigate the four-dimensional topology of its space, just as pulling on
a two-dimensional noose tied round the Earth or a coffee cup handle allows
us to investigate their topologies.
The Ricci flow is a way of resolving a 3-manifold into its simplest form
by moving the points on the surface, but without "tearing" it. just as a
coffee cup could be warped into a simpler doughnut shape without tearing
the fabric, the Ricci flow was a four-dimensional shape into a simpler one
while keeping the same topology. Hamilton's idea was to demonstrate that
no matter what surface you start with, you always end up with a combination
of Thurston's primes. The Poincaré hypothesis would follow because
the Ricci flow would warp any surface on which you can draw a loop to a point
into a 3-sphere or combination of 3-spheres. However, Hamilton ran into a
problem. In some cases, instead of flowing smoothly to a simpler form parts
of a manifold could collapse away to nothing. Imagine a piece of chewing
gum being stretched out, forming an elongated neck that thins away to almost
nothing. There is no way to demonstrate anything about the topology of the
thin neck or singularity", because the Ricci flow cannot warp something that
is infinitely thin.
| The new proof by Grigori Perelman relies on a technique called the Ricci flow, which warps three-dimensional surfaces into their simplest components | |
| One problem with the new proof is that during warping, part of the surface may thin away to nothing, creating a 'singularity ' | 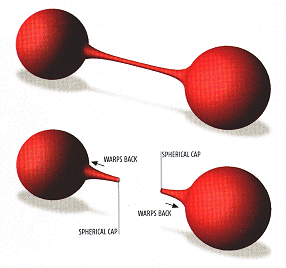 |
| Perelman shows how to perform surgery on the singularities, cutting them not and capping them off. The result is simple shapes with topology equivalent lent to the original | |
"When a proof falls apart, someone tries to
fill the gap and something else pops up. There is a clear downward trajectory.
That simply hasn't happened"
And this is where Perelman stepped in. His first
paper, released online in November 2002, applied Hamilton's ideas to the
case in which no singularities arise. The paper was pored over by mathematicians
at a conference in December 2003, and according to Bruce Kleiner of the
University of Michigan, Ann Arbor, was "essentially confirmed, except possibly
for some minor points". Those points, according to Kleiner, have since been
verified.
Perelman's second paper, posted online in July 2003, is technically much
more challenging. It takes on the dangerous singularities. He shows that
the area around any looming singularity in a surface can be cut away and
"capped off". Perelman's proof cuts out any part of the surface that is shooting
off to infinity, and shows that the edges of the cut he has made can be precisely
mapped to a simple cap, which is a sphere (see Graphic, above). "It's like
a plumber might do if it was a pipe and he didn't want water seeping out,"
Morgan says.
Performing these cuts involves exceptionally complicated calculations to
show that the edges of the cap always match up exactly with the cut on the
surface. But they seem to be right. "The argument is fairly complicated,"
Kleiner says. "But to date nobody has found any mistakes beyond a few typos!"
But it may not be necessary for Perelman to prove the geometrisation conjecture
in order to claim his million dollars. "He claims to understand all
three-dimensional spaces, but the Poincaré conjecture is simpler,
and to prove it you don't actually use everything he had to establish for
the geometrisation conjecture," Morgan says. Kleiner, though, says he won't
be ready to concede that Poincaré is solved until the geometrisation
conjecture has been proved and Poincaré derived directly from it.
This will take some time. Before Perelman can claim the Clay prize, his proof
needs to be published in a peer-reviewed journal - which will take several
months even after the checking process is complete. But Jim Carison of the
Clay Institute says the institute has already formed a committee to track
the proof's progress and things are looking good. "When a proof falls apart,
people find little problems, someone tries to fill the gap and something
else pops up. There is a clear downward trajectory," Carison says. "That
simply hasn't happened in this case.
" In November 2003, Hamilton told a packed meeting at the Clay Institute
that he thought the details of Perelman's proof were going to come out right.
As the inventor of the Ricci flow, Hamilton said he had always hoped that
the singularities could be cut out in some way. He gave up when he began
to suspect that infinitely many singularities could form during the warping
process of Ricci flows, making it impossible to prove the Poincaré
conjecture. But Hamilton admitted that he now thinks singularities in a surface
form at a rate that can be controlled, and that Perelman was right to press
on: the singularities can be cut out and neutralised.
If verified, the proof will mean more than relief for Hamilton, and the others
afflicted with Poincaritis. The tools Hamilton and Perelman have used to
prove the conjecture may have implications in general relativity, in which
matter and energy warp the fabric of space-time,
sometimes producing perplexing singularities. They will also allow mathematicians
to apply the Ricci flow to other problems in topology, without the threat
of singularities ruining their calculations. But for most of us, there is
a greater prize. If Perelman is right, we will finally be able to say that
our instinctive understanding of three dimensional space is spot on. And
we all like to be proved right, don't we?
Bruce Schechter is a writer in New York City
