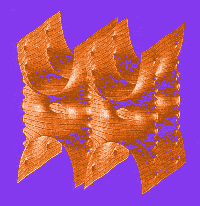Absolute Certainty?
 |
|
| "VIDEO PROOF" [See Video N25] dramatizes a theorem, proved by William P. Thurston of the Mathematical Sciences Research Institute (left), that establishes a profound connection between topology and geometry. The theorem shows how the space surrounding a complex knot (represented by the lattice in this scene) yields a "hyperbolic" geometry, in which parallel lines diverge and the sides of pentagons form right angles.The computer- generated video, called Not Knot, was produced at the Geometry Center in Minnesota. |
Computers are transforming the way mathematicians discover,prove and
communicate ideas,but is there a place for absolute certainty in this brave
new world?
Legend has it that when
Pythagoras and his followers discovered the theorem
that bears his name in the sixth century B.C., they slaughtered an ox and
feasted in celebration. And well they might. The relation they found between
the sides of a right triangle held true not sometimes or most of the time
but always-regardless of whether the triangle was a piece of silk or a plot
of land or marks on papyrus. It seemed like magic,
a gift from the gods. No wonder so many thinkers, from
Plato to
Kant, came to believe that mathematics offers
the purest truths humans are permitted to know.
That faith seemed reaffirmed this past June when
Andrew J. Wiles of Princeton University
revealed during a meeting at the University of Cambridge that he had solved
Fermat's last theorem. This problem, one of the
most famous in mathematics, was posed more than 350 years ago, and its roots
extend back to Pythagoras himself. Since no oxen were available, Wiles's
listeners showed their appreciation by clapping their hands.
But was the proof of Fermat's last theorem
the last gasp of a dying culture? Mathematics, that most tradition-bound
of intellectual enterprises, is undergoing profound changes. For millennia,
mathematicians have measured progress in terms of what they can demonstrate
through proofs-that is, a series of logical steps leading from a set of axioms
to an irrefutable conclusion. Now the doubts riddling modern human thought
have finally infected mathematics. Mathematicians may at last be forced to
accept what many scientists and philosophers already have admitted: their
assertions are, at best, only provisionally true, true until proved
false.
This uncertainty stems, in part, from the growing complexity of mathematics.
Proofs are often so long and complicated that they are difficult to evaluate.
Wiles's demonstration runs to 200 pages-and experts estimate it could be
five times longer if he spelled out all its elements. One observer asserted
that only one tenth of 1 percent of the mathematics community was qualified
to evaluate the proof.Wiles's claim was accepted largely on the basis of
his reputation and the reputations of those whose work he built on.
Mathematicians who had not yet examined the argument in detail nonetheless
commented that it "looks beautiful" and "has the ring of truth."
Another catalyst of change is the computer, which is compelling mathematicians
to reconsider the very nature of proof and, hence,
of truth- In recent years, some proofs have required enormous calculations
by computers. No mere human can verify these so-called computer proofs, just
other computers. Recently investigators have proposed a computational proof
that offers only the probability - not the certainty - of truth, a statement
that some mathematicians consider an oxymoron. Still others are generating
"video proofs" in the hopes that they will be more persuasive than page on
page of formal terminology.
At the same time, some mathematicians are challenging the notion that formal
proof should be the supreme standard of truth. Although no one advocates
doing away with proofs altogether, some practitioners think the validity-
of certain propositions may be better established by comparing them with
experiments run on computers or with real-world phenomena. "Within the next
50 years I think the importance of proof in mathematics will diminish," says
Keith Devlin of Colby College, who writes a column on computers for Notices
of the American Mathematical Society. "You will see many more people
doing mathematics without necessarily doing proofs."
Powerful institutional forces are promulgating these heresies. For several
years, the National Science Foundation has been urging mathematicians to
become more involved in computer science and other fields with potential
applications. Some leading lights, notably Phillip A. Griffiths, director
of the Institute for Advanced Study in Princeton, N.J., and Michael Atiyah,
who won a Fields Medal (often called the Nobel Prize of mathematics) in 1966
and now heads Cambridge's Isaac Newton Institute for Mathematical Sciences,
have likewise encouraged mathematicians to venture forth from their ivory
towers and mingle with the real world. At a time when funds and jobs are
scarce, young mathematicians cannot afford to ignore these exhortations.
There are pockets of resistance, of course. Some workers are complaining
bitterly about the computerization of their field and the growing emphasis
on (oh, dirty word) "applications." One (if the most vocal champions of tradition
is Steven G. Krantz. of Washington University. In speeches and articles,
Krantz has urged students to choose mathematics over computer science, which
he warns could be a passing fad. Last year, he recalls, a National Science
Foundation representative came to his university- and announced that the
agency could no longer afford to support mathematics that was not
"goal-oriented." "We could stand up and say this is wrong, Krantz grumbles,
"but mathematicians are spineless slobs, and they don't have a tradition
of doing that."
David Mumford of Harvard University, who won a Fields Medal in 1974 for research
in pure mathematics and is now studying artificial vision, wrote recently
that "despite all the hype, the press, the pressure from funding agencies,
et cetera, the pure mathematical community by and large still regards computers
as invaders, despoilers of the sacred ground." Last year Mumford proposed
a course in which instructors would show students how to program a computer
to find solutions in advanced calculus. "I was vetoed," he recalled, "and
not on the grounds-which I expected-that the students would complain, but
because half of my fellow teachers couldn't program!"
A Splendid Anachronism? |
|
 |
Those who consider experimental mathematics and computer
proofs to be abominations rather than innovations have a special reason to
delight in the conquest of
Fermat's last
theorem by Andrew Wiles of Princeton University.
Wiles's achievement was a triumph of tradition, running against every current
in modern mathematics. Wiles is a staunch believer in mathematics for its own sake. "I certainly wouldn't want to see mathematics just being a servant to applications, because it's not even in the interests of the applications themselves," he says. |
| The problem he solved, first posed more than
350 years ago by the French polymath
Pierre de Fermat, is a glorious example of a
purely mathematical puzzle. Fermat claimed to have found a proof of the following
proposition: for the equation XN + YN = ZN,
there are no integral solutions for any value of N greater than 2. The efforts
of mathematicians to find the proof (which Fermat never did disclose) helped
to lay the foundation of modern number theory, the study of whole numbers,
which has recently become useful in cryptography.Yet Fermat's last theorem
itself "is very unlikely to have any applications," Wiles says. Although funding agencies have been encouraging mathematicians to collaborate, both with each other and with scientists, Wiles worked in virtual solitude for seven years. He shared his ideas with only a few colleagues toward the end of his quest. Wiles's proof has essentially the same classical, deductive form that Euclid's geometric theorems did. It does not involve any computation, and it claims to be absolutely -not probably-true. Nor did Wiles employ computers to represent ideas graphically, to perform calculations or even to compose his paper; a secretary typed his hand-written notes. He concedes that testing conjectures with computers may be helpful. In the 1970s computer tests suggested that a far-fetched proposal called the Taniyama conjecture might be true. The tests spurred work that laid the foundation for Wiles's own proof. Nevertheless, Wiles doubts he will take the trouble to learn how to perform computer investigations. "It's a separate skill," he explains, "and if you're investing that much time on a separate skill, it's quite likely it's taking you away from your real work on the problem." He rejects the possibility that there may be a finite number of truths accessible to traditional forms of inquiry. "I disagree vehemently with the idea that good theorems are running out," he says. "I think we've barely scratched the surface." |
|
That situation is changing fast, if the University of Minnesota's Geometry
Center is any indication. Founded two years ago, the Geometry Center occupies
the fifth floor of a gleaming, steel and glass polyhedron in Minneapolis.
It receives $2 million a year from the National Science Foundation, the
Department of Energy and the university. The center's permanent faculty members,
most of whom hold positions elsewhere, include some of the most prominent
mathematicians in the world.
On a recent day there, several young staff members are editing a video
demonstrating how a sphere can be mashed, twisted, yanked and finally turned
inside out. In a conference room, three computer scientists from major
universities are telling a score of high school teachers how to create computer
graphics programs to teach mathematics. Other researchers sit at charcoal-colored
NeXT terminals, pondering luridly hued pictures of four-dimensional "hypercubes,"
whirlpooling fractals and lattices that plunge toward infinity. No paper
or pencils are in sight.
At one terminal is David Ben-Zvi, a Harpo Marx-haired junior at Princeton
who is spending six months here exploring nonlinear dynamics. He dismisses
the fears of some mathematicians that computers will lure them away from
the methods that have served them so well for so long. "They're just afraid
of change," he says mildly.
The Geometry Center is a hotbed of what is known as experimental mathematics,
in which investigators test their ideas by representing them graphically
and doing calculations on computers. Last year some of the center's faculty
helped to found a journal, Experimental Mathematics, that showcases
such work. "Experimental methods are not a new thing in mathematics," observes
the journal's editor, David B. A. Epstein of the
University of Warwick in England,
noting that Carl Fredrich Gauss and other giants often performed experimental
calculations before constructing formal proofs. "What's new is that it's
respectable." Epstein acknowledges that not all his co-workers are so accepting.
"One of my colleagues said, 'Your journal should be called the Journal
of Unproved Theorems.'"
Bubbles and Tortellini
A mathematician who epitomizes the new style of mathematics is Jean E. Taylor
of Rutgers University. "The idea that you don't use computers is going to
be increasingly foreign to the next generation," she says. For two decades,
Taylor has investigated minimal surfaces, which
represent the smallest possible area or volume bounded by a curve or surface.
Perhaps the most elegant and simple minimal surfaces found in nature are
soap bubbles and films. Taylor has always had an experimental bent. Early
in her career she tested her handwritten models of minimal surfaces by dunking
loops of wire into a sink of soapy water.
|
 |
| EXPERIMENTAL MATHEMATICIAN Jean E. Taylor of Rutgers University seeks the rules governing minimal surfaces by studying real phenomena, such as soap bubbles, and computer-generated ones, such as idealized crystals (above). | |
Now she is more likely to model bubbles with a sophisticated
computer graphics program. She has also graduated from soap bubbles to
crystals, which conform to somewhat more complicated rules about minimal
surfaces. Together with Frederick J. Almgren of Princeton and Robert
F. Almgren of the University of Chicago (her husband and stepson, respectively)
and Andrew R. Roosen of the National Institute of Standards and Technology,
Taylor is trying to mimic the growth of
snowflakes and
other crystals on a computer. Increasingly, she is
collaborating with materials scientists and physicists, swapping mathematical
ideas and programming techniques in exchange for clues about how real crystals
grow.
Another mathematician who has prowled cyberspace in search of novel minimal
surfaces is David A. Hoffman of the University of Massachusetts at Amherst.
Among his favorite quarry are catenoids and helicoids, which resemble the
pasta known as tortellini and were first discovered in the 18th century.
"We gain a tremendous amount of intuition by looking at images of these surfaces
on computers," he says.
In 1992 Hoffman, Fusheng Wei of Amherst and Hermann Karcher of the University
of Bonn speculated on the existence of a new class of helicoids, ones with
handles. They succeeded in representing these helicoids-the first discovered
since the 18th century-on a computer and went on to produce a formal proof
of their existence. "Had we not been able to see a picture that roughly
corresponded to what we believed, we would never have been able to do it,"
Hoffman says.
The area of experimental mathematics that has received the lion's share of
attention over the past decade is known as
nonlinear dynamics or, more popularly,
chaos. In general, nonlinear systems are governed
by a set of simple rules that, through feedback and related effects, give
rise to complicated phenomena. Nonlinear systems were investigated in the
precomputer era, but computers allow mathematicians to explore these systems
and watch them evolve in ways that
Henri Poincaré and other pioneers
of this branch of mathematics could not.
Cellular automata, which divide
a computer screen into a set of cells (equivalent to pixels), provide a
particularly dramatic illustration of the principle of nonlinearity. In general,
the color, or "state," of each cell is determined by the state of its neighbors.
A change in the state of a single cell triggers a cascade of changes throughout
the system.
One of the must celebrated of cellular automata was invented by
John H. Conway of Princeton in the early 1970s.
Conway has proved that his automaton, which he calls
"Life," is "undecidable":
one cannot determine whether its patterns are endlessly variegated or eventually
repeat themselves. Scientists have seized on cellular automata as tools for
studying the origin and evolution of life. The computer scientist and physicist
Edward Fredkin of Boston University has even argued that the entire universe
is a cellular automaton.
More famous still is the
Mandelbrot set,
whose image has become an icon for the entire field of chaos since it was
popularized in the early 1980s by Benoit B. Mandelbrot
of the IBM Thomas J. Watson Research Center. The set stems from a simple
equation containing a complex term (based on the square root of a negative
number). The equation spits out solutions, which are then iterated, or fed
back, into the equation. The mathematics underlying the set had been invented
more than 70 years ago by two Frenchmen,
Gaston Julia and Pierre Fatou, but computers
laid bare their baroque beauty for all to see. When plotted on a computer,
the Mandelbrot set coalesces into an image that has been likened to a tumorous
heart, a badly burned chicken and a warty snowman. The image is a
fractal: its
fuzzy borders are infinitely long. and it displays patterns that recur at
different scales.
Researchers are now studying sets that are similar to the Mandelbrot set
but inhabit four dimensions. The kinds of complications you get here are
the kinds you get in many different sciences," says John Milnor of the State
University of New York at Stony Brook. Milnor is trying to fathom the properties
of the four-dimensional set by examining two- dimensional slices of it generated
by a computer. His preliminary findings led off he inaugural issue of
Experimental Mathematics last year. Milnor, a 1962 Fields Medalist,
says he occasionally performed computer experiments in the days of punch
cards, but "it was a miserable process. It has become much easier."
 |
HELICOID WITH A HOLE (bottom left) was discovered last year by David A. Hoffman of the University of Massachusetts at Amherst and his colleagues with the help of computer graphics. Edward C. Thayer, one of Hoffman's graduate students, recently found a structure (below) that mimics the pattern of certain polymers. |
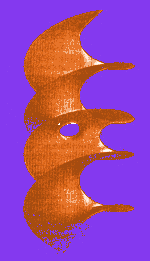 |
|
The popularity of graphics-oriented mathematics has provoked
a backlash. Krantz of Washington University charged four years ago in the
Mathematical Intelligencer that "in some circles, it is easier to
obtain funding to buy hardware to generate pictures of fractals than to obtain
funding to study algebraic geometry."
A broader warning about "speculative" mathematics was voiced this past July
in the Bulletin of the American Mathematical Society by Arthur Jaffe
of Harvard and Frank S. Quinn of the Virginia Polytechnic Institute. They
suggested that computer experiments and correspondence with natural phenomena
are no substitute for proofs in establishing truth. "Groups and individuals
within the mathematics community have from time to time tried being less
compulsive about details of arguments," Jaffe and Quinn wrote. "The results
have been mixed, and they have occasionally been disastrous."
Most mathematicians exploiting computer graphics and other
experimental techniques agree that seeing should not be believing and that
proofs are still needed to verify the conjectures they arrive at through
computation. "I think mathematicians were contemplating their navels for
too long, but that doesn't mean I think proofs are irrelevant," Taylor says.
Hoffman offers an even stronger defense of traditional proofs. "Proofs are
the only laboratory instrument mathematicians have," he remarks, "and they
are in danger of being thrown out." Although computer graphics are "unbelievably
wonderful," he adds, "in the 1960s drugs were unbelievably wonderful, and
some people didn't survive."
Indeed, veteran computer enthusiasts know better than most that computational
experiments-whether involving graphics or numerical calculations- can be
deceiving. One cautionary tale involves the
Riemann hypothesis, a famous prediction
about the patterns displayed by
prime numbers as they march toward
infinity. First posed more than 100 years ago by
Bernhard Riemann, the hypothesis is considered
to be one of the most important unsolved problems in mathematics.
A contemporary of Riemann's, Franz Mertens, proposed a related conjecture
invoking positive whole numbers; if true, the conjecture would have provided
strong evidence that the
Riemann hypothesis
was also true. By the early 1980s computers had shown that Mertens's
proposal did indeed hold for at least the first 10 billion integers. In 1984,
however, more extensive computations revealed that eventually-at numbers
as high as 101070-the pattern predicted by Mertens
vanishes.
One potential drawback of computers is that all their calculations are based
on the manipulation of discrete, whole numbers-in fact, ones and zeros. Computers
can only approximate real numbers, such as pi or the square root of two.
Someone knowledgeable about the rounding-off functions of a simple pocket
calculator can easily induce it to generate incorrect answers to calculations.
More sophisticated programs can make more complicated and elusive errors.
In 1991 David R. Stoutemyer, a software specialist at the University of Hawaii,
presented 18 experiments in algebra that gave wrong answers when performed
with standard mathematics software.
 UNEARTHLY LANDSCAPES emerge
when a computer generates "slices" of a four- dimensional map similar to
the well-known Mandelbrot set. John Milnor of the State University of New
York at Stony Brook studies similar two-dimensional images in order to understand
the properties of the complex mathematical object. UNEARTHLY LANDSCAPES emerge
when a computer generates "slices" of a four- dimensional map similar to
the well-known Mandelbrot set. John Milnor of the State University of New
York at Stony Brook studies similar two-dimensional images in order to understand
the properties of the complex mathematical object. |
|
 |
 |
Stephen Smale of the University of California at Berkeley,
a 1966 Fields Medalist, has sought to place mathematical computation on a
more secure foundation-or at least to point out the size and location of
the cracks running through the foundation. Together with Lenore Blum of the
Mathematical Sciences Research Institute at Berkeley and Michael Shub of
IBM, he has created a theoretical model of a computer that can process real
numbers rather than just integers.
Blum and Smale recently concluded that the Mandelbrot set is, in a technical
sense, uncomputable.That is, one cannot determine with certainty whether
any given point on the complex plane resides within or outside the set's
hirsute border. These results suggest that "you have to be careful" in
extrapolating from the results of computer experiments, Smale says.
These concerns are dismissed by Stephen Wolfram, a mathematical physicist
at the University of Illinois. Wolfram is the creator of Mathematical, which
has become the leading mathematics software since first being marketed five
years ago. He acknowledges that "there are indeed pitfalls in experimental
mathematics. As in all other kinds of experiments, you can do them wrong."
But he emphasizes that computational experiments, intelligently performed
and analyzed, can yield more results than the old-fashioned conjecture- proof
method. "In every other field of science there are a lot more experimentalists
than theorists," Wolfram says. "I suspect that will increasingly be the case
with mathematics."
"The obsession with proof," Wolfram declares, has kept mathematicians from
discovering the vast new realms of phenomena accessible to computers. Even
the most intrepid mathematical experimentalists are for the most part "not
going far enough," he says. "They're taking existing questions in mathematics
and investigating those. They are adding a few little curlicues to the top
of a gigantic structure."
Mathematicians may take this view with a grain of salt. Although he shares
Wolfram's fascination with cellular automata, Conway contends that Wolfram's
career-as well as his contempt for proofs-shows he is not a real mathematician.
"Pure mathematicians usually don't found companies and deal with the world
in an aggressive way,Life's creator says.We sit in our ivory towers and think
about things."
Purists may have a harder time ignoring William P. Thurston, who is also
an enthusiastic booster of experimental mathematics and of computers in
mathematics. Thurston, who heads the Mathematical Sciences Research Institute
at Berkeley and is a co-director of the Geometry Center (with Albert Marden
of the University of Minnesota), has impeccable credentials. In the mid-1970s
he pointed out a deep potential connection between two separate branches
of mathematics-topology and geometry.
Thurston won a Fields Medal for this work in 1982. Thurston emphasizes that
he believes mathematical truths are discovered and not invented. But on the
subject of proofs, he sounds less like a disciple of Plato than
of Thomas S. Kuhn, the philosopher
who argued in his 1962 book, The Structure of Scientific Revolution,
that scientific theories are accepted for social reasons rather than because
they are in any objective sense "true." "That mathematics reduces in principle
to formal proofs is a shaky idea" peculiar to this century, Thurston asserts.
"In practice, mathematicians prove theorems in a social context," he says.
"It is a socially conditioned body of knowledge and techniques."
 |
| PARTY PROBLEM was solved after a vast computation by Stanislaw P. Radziszowski and Brendan D. McKay. They calculated that at least 25 people are required to ensure either that four people are all mutual acquaintances or that five are mutual strangers. This diagram, in which red lines connect friends and yellow lines link strangers, shows that a party of 24 violates the dictum. |
The logician Kurt
Gödel demonstrated more than 60 years ago through his incompleteness
theorem that "it is impossible to codify mathematics," Thurston notes. Any
set of axioms yields statements that are self-evidently true but cannot be
demonstrated with those
axioms. Bertrand Russell
pointed out even earlier that set theory, which is the basis of much of
mathematics, is rife with logical
contradictions related to the problem of self-reference. (The self-
contradicting statement "This sentence is false" illustrates the problem.)
"Set theory is based on polite lies, things we agree on even though we know
they're not true," Thurston says. "In some ways, the foundation of mathematics
has an air of unreality."
Thurston thinks highly formal proofs are more likely to be flawed than those
appealing to a more intuitive level of understanding. He is particularly
enamored of the ability of computer graphics to communicate abstract mathematical
concepts to others both within and outside the professional community. Two
years ago, at his urging, the Geometry Center produced a computer-generated
"video proof," called Not Knot, that dramatizes
a ground-breaking conjecture he proved a decade ago. Thurston mentions proudly
that the rock band the Grateful Dead has shown the Not Knot video at its
concerts.
Whether Deadheads grok the substance of the video-which concerns how mathematical
objects called three- manifolds behave in a
non-Euclidean
"hyperbolic" space-is another matter. Thurston concedes that the video is
difficult for nonmathematicians, and even some professionals, to fathom,
but he is undaunted. The Geometry Center is now producing a video of yet
another of his theorems, which demonstrates how a sphere can be turned inside
out. Last fall, moreover, Thurston organized a workshop at which participants
discussed how virtual reality and other advanced technologies could be adapted
for mathematical visualization.
Paradoxically, computers have catalyzed a countertrend in which truth is
obtained at the expense of comprehensibility. In 1976 Kenneth Appel and Wolfgang
Haken of the University of Illinois claimed they had proved the
four-color conjecture, which stated that four
hues are sufficient to construct even an infinitely broad
map so that no identically colored countries share
a border. In some respects, the proof of Appel and Haken was conventional-that
is, it consisted of a series of logical, traceable steps proceeding to a
conclusion. The conclusion was that the conjecture could be reduced to a
prediction about the behavior of some 2,000 different maps.
Since checking this prediction by hand would be prohibitively time-consuming,
Appel and Haken programmed a computer to do the job for them. Some 1,000
hours of computing time later, the machine concluded that the 2,000 maps
behave as expected: the four-color
conjecture was true.
The Party Problem
Other computer-assisted proofs have followed. Just this year, a proof of
the so-called party problem was announced by Stanislaw
P. Radziszowski of the Rochester Institute of Technology and Brendan D. McKay
of the Australian National University in Canberra. The problem, which derives
from work in set theory by the British mathematician Frank P. Ramsey in the
1920s, can be phrased as a question about relationships between people at
a party. What is the minimum number of guests that must be invited to guarantee
that at least X people are all mutual acquaintances or at least Y are mutual
strangers? This number is known as a Ramsey number.
Previous proofs had established that 18 guests are required to ensure that
there are either four mutual acquaintances or four strangers. In their proof,
Radziszowski and McKay showed that the Ramsey number for four friends or
five strangers is 25. Socialites might think twice about trying to calculate
the Ramsey number for greater X's and Y's. Radziszowski and McKay estimate
that their proof consumed the equivalent of 11 years of computation by a
standard desktop machine. That may be a record, Radziszowski says, for a
problem in pure mathematics.
The value of this work has been debated in an unlikely forum-the news- paper
column of advice-dispenser Ann Landers. In June a correspondent complained
to Landers that resources spent on the party problem should have been used
to help "starving children in wartorn countries around the world." Some
mathematicians raise another objection to computer-assisted proofs. "I don't
believe in a proof done by a computer, says Pierre Deligne of the Institute
for Advanced Study, an algebraic geometer and 1978 Fields Medalist. "In a
way, I am very egocentric. I believe in a proof if I understand it, if it's
clear." While recognizing that humans can make mistakes, he adds: "A computer
will also make mistakes, but they are much more difficult to find."
Silicon Mathematicians |
| The continuing penetration of computers into mathematics
has revived an old debate: Can mathematics be entirely automated? Will the
great mathematicians of the next century be made of silicon? In fact, computer scientists have been working for decades on programs that generate mathematical conjectures and proofs. In the late 1950s the artificial-intelligence guru Marvin Minsky showed how a computer could "rediscover" some of Euclid's basic theorems in geometry. In the 1970's Douglas Lenat, a former student of Minsky's, presented a program that devised even more advanced geometry theorems. Skeptics contended that the results were, in effect, embedded in the original program. A decade ago the computer scientist and entrepreneur Edward Fredkin sought to revive the sagging interest in machine mathematics by creating what came to be known as the Leibniz Prize. The prize, administered by Carnegie Mellon University, offers $100,000 for the first computer program to devise a theorem that has a "profound effect" on mathematics.Some practitioners of what is known as automated reasoning think they may be ready to claim the prize. One is Larry Wos of Argonne National Laboratory, editor of the Journal of Automated Reasoning.He claims to have developed a program that has solved problems in mathematics and logic "that have stumped people for years." Another is Siemeon Fajtlowicz of the University of Houston, inventor of a program, called Graffiti, that has proposed "thousands" of conjectures in graph theory. None of these achievements comes close to satisfying the "profound effect" criterion, according to David Mumford of Harvard University, a judge for the prize. "Not now, not 100 years from now," Mumford replies when asked to predict when the prize might be claimed. Some observers think computers will eventually surpass our mathematical abilities. After all, notes Ronald L. Graham of AT & T Bell Laboratories, "we're not very well adapted for thinking about the space-time continuum or the Riemann hypothesis. We're designed for picking berries or avoiding being eaten." Others side with the mathematical physicist Roger Penrose of the University of Oxford, who in his 1989 book, The Emperor's New Mind, asserted that computers can never replace mathematicians. Penrose's argument drew on quantum theory and Gödel's incompleteness theorem, but he may have been most convincing when discussing his personal experience. At its best, he suggested, mathematics is an art, a creative act, that cannot be reduced to logic any more than King Lear or Beethoven's Fifth can. |
Others take a more functional point of view, arguing that
establishing truth is more important than giving mathematicians an aesthetic
glow, particularly if a result is ever to find an application. Defenders
of this approach, who tend to be computer scientists, point out that conventional
proofs are far from immune to error. At the turn of the century, most theorems
were short enough to read in one sitting and were produced by a single author.
Now proofs often extend to hundreds of pages or more and are so complicated
that years may pass before they are confirmed by others.
The current record holder of all conventional proofs was completed in the
early 1980s and is called the classification of finite, simple groups.
(A group is a set of
elements, such as integers, together with an operation, such as addition,
that combines two elements to get a third one.) The demonstration consists
of some 500 articles totaling nearly 15,000 pages and written by more than
100 workers. It has been said that the only person who grasped the entire
proof was its general contractor, Daniel Gorenstein of Rutgers. Gorenstein
died last year.
Much shorter proofs can also raise doubts. Three years ago Wu-Yi Hsiang of
Berkeley announced he had proved an old conjecture that one can pack the
most spheres in a given volume by stacking them like cannonballs. Today some
skeptics are convinced the 100- page proof is flawed; others are equally
certain it is basically correct.
Indeed, the key to greater reliability, according to some computer scientists,
is not less computerization but more. Robert S. Boyer of the University of
Texas at Austin has led an effort to squeeze the entire sprawling corpus
of modern mathematics into a single data base whose consistency can be verified
through automated "proof checkers."
The manifesto of the so-called QED Project states that such a data base will
enable users to "scan the entirety of mathematical knowledge for relevant
results and, using tools of the QED system, build upon such results with
reliability and confidence but without the need for minute comprehension
of the details or even the ultimate foundations." The QED system, the manifesto
proclaims rather grandly, can even "provide some antidote to the degenerative
effects of cultural relativism and nihilism" and, presumably, protect mathematics
from the all-too-human willingness to succumb to fashion.
The debate over computer proofs has intensified recently with the advent
of a technique that offers not certainty but only a statistical probability
of truth. Such proofs exploit methods similar to those underlying
error-correction codes, which ensure that transmitted messages are
not lost to noise and other effects by making them highly redundant. The
proof must first be spelled out precisely in a rigorous form of mathematical
logic. The logic then undergoes a further transformation called arithimetization,
in which "and," "or" and other functions are translated into arithmetic
operations, such as addition and multiplication.
Like a message transformed by an error-correction code, the "answer" of a
probabilistic demonstration is distributed throughout its length-as are any
errors. One checks the proof by querying it at different points and determining
whether the answers are consistent; as the number of checks increases, so
does the certainty that the argument is correct. Laszlo Babai of the University
of Chicago, who developed the proofs two years ago (along with Lance Fortnow,
Carsten Lund and Mario Szegedy of Chicago and Leonid A. Levin of Boston
University), calls them "transparent." Manuel Blum of Berkeley, whose work
helped to pave the way for Babai's group, suggests the term "holographic."
The Uncertain Future
Whatever they are named, such proofs have practical drawbacks. Szegedy
acknowledges that transforming a conventional demonstration into the
probabilistic form is difficult, and the result can be a "much bigger and
uglier animal." A 1,000-line proof, for example, could easily balloon to
1,0003 (1,000,000,000) lines. Yet Szegedy contends that if he
and his colleagues can simplify the transformation process, probabilistic
proofs might become a useful method for verifying mathematical propositions
and large computations-such as those leading to the
four-color theorem. "The philosophical cost
of this efficient method is that we lose the absolute certainty of a Euclidean
proof," Babai noted in a recent essay. "But if you do have doubts, will you
bet with me?"
Such a bet would be ill advised, Levin believes, since a relatively few checks
can make the chance of error vanishingly small: one divided by the number
of particles in the universe. Even the most straightforward conventional
proofs, Levin points out, are susceptible to doubts of this scale. "At the
moment you find an error, your brain may disappear because of
the Heisenberg uncertainty
principle and be replaced by a new brain that thinks the proof is correct,"
he says.
Ronald L. Graham of AT & T Bell Laboratories suggests that the trend
away from short, clear, conventional proofs that are beyond reasonable doubt
may be inevitable. "The things you can prove may be just tiny islands,
exceptions, compared to the vast sea of results that cannot be proved by
human thought alone," he explains. Mathematicians seeking to navigate uncharted
waters may become increasingly dependent on experiments, probabilistic proofs
and other guides. "You may not be able to provide proofs in a classical sense,"
Graham says.
Of course, mathematics may yield fewer aesthetic satisfactions as investigators
become more dependent on computers. "It would be very discouraging," Graham
remarks, "if somewhere down the line you could ask a computer if the Riemann
hypothesis is correct and it said, 'Yes, it is true, but you won't be able
to understand the proof.'"
Traditionalists no doubt shudder at the thought. For now, at least, they
can rally behind heros like Wiles, the conqueror of Fermat's last theorem,
who eschews computers, applications and other abominations. But there may
be fewer Wileses in the future if reports from the front of precollege education
are any guide. The Mathematical Sciences Research institute at Berkeley,
which is overseen by Thurston, has been holding an ongoing series of seminars
with high school teachers to find new ways to entice students into mathematics.
This past January Lenore Blum, the institute's deputy director, organized
a seminar devoted to the question "Are Proofs in High School Geometry
Obsolete?"
The mathematicians insisted that proofs are crucial to ensure that a results
is true. The high school teachers demurred, pointing out that students no
longer considered traditional, axiomatic proofs to be as convincing as, say,
visual arguments. "The high school teachers overwhelmingly declared that
most students now (Nintendo/joystick/MTV generation) do not relate to or
see the importance of 'proofs,'" the minutes of the meeting stated. Note
the quotation marks around the word "proofs."