 |
Finding the energy to solve a knotty problem
|
For at least a century, mathematicians have tried to find
effective ways to distinguish between different
knots. Until recently, the only methods available
had been introduced in the 1920s. But in the 1980s the subject was revolutionised
by the discovery of the "Jones polynomial" by Vaughan Jones, a New Zealand
mathematician. Now a third line of attack is opening up, based on physical
considerations about the energy of knots.
Distinguishing between knots is an important problem - not
because of what it tells us about knots of the boy scout variety, but because
it represents the simplest and most natural instance of a very general problem:
how to tell the difference between different ways of embedding one space
in another. This problem crops up in a variety of guises all over mathematics.
Also, practical applications of knot theory exist in problems as diverse
as Feynman
diagrams in quantum physics and the cutting
of DNA molecules by enzymes. But to
mathematicians the real allure of knots is their unexpected subtlety, and
how such an apparently simple task as distinguishing between two knots can
lead to powerful new techniques.
In mathematics, a knot is defined as a closed loop in
three-dimensional space- like a piece of string with its ends glued together.
Two knots are "the same"- that is topologically equivalent - if,by stretching
and bending the space that surrounds them, one can be deformed into the other.
Any loop that deforms into a circle is termed unknotted, whereas all other
loops are genuine knots. It is this freedom to deform knots that makes them
so subtle: in order to prove that two knots are different, mathematicians
must rule out all conceivable deformations that might make them the same.
All known methods of proving knots to be different boiled
down to finding "invariants" -properties that remain unchanged by deformations.
Two knots that have different invariants must be topologically different.
The key invariant of the 1920s - the classical period of knot theory - was
discovered by J. W. Alexander, an American mathematician. The Alexander
polynomial is an algebraic expression associated with any knot. Knots whose
Alexander polynomials are different cannot be deformed into each other.
Unfortunately, the converse is not true: knots with the same Alexander polynomial
need not be topologically equivalent. The simplest examples are the reef
and granny knots, which have identical Alexander polynomials though they
are topologically different.
The Jones polynomial is superficially similar, but was reached
by a very different route -via mathematical physics. It often succeeds where
the Alexander polynomial fails. In particular, the Jones polynomial of a
reef knot is different from that of a granny knot, providing logically impeccable
confirmation of what generations of boy scouts already know - that it does
matter which one you use.
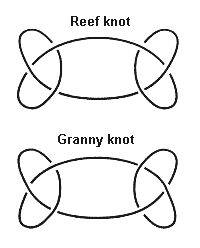 |
| The reef and granny knots have identical Alexander polynomials although they are topologically different. |
The new method of distinguishing between knots relies not on
a polynomial, but on a number as invariant. The underlying idea goes back
to work done by I. Fary in 1929. Imagine tying a knot in a long rubber rod.
The more complicated the knot, the more you have to bend the rod to tie it,
so the more elastic energy it acquires.
But it now looks as if the most interesting "energy" concept
for knots is not elastic, but electrostatic, as suggested in 1987 by S. Fukuhara
of Tsuda College, Tokyo. Imagine the knot to be a flexible wire of fixed
length, which can pass through itself if necessary and which has a uniform
electrostatic charge along its length. Because like charges repel each other,
a knot that is free to move will arrange itself so as to keep neighbouring
strands as far apart as possible in order to minimise its electrostatic energy.
This minimum energy value is the invariant.
But is it a useful one? Does it have simple, natural properties
that mathematicians can exploit? In 1991, Jun O'Hara of Tokyo Metropolitan
University proved that the minimum energy of a knot really does increase
as the knot becomes more complicated. Only a finite number of topologically
different knots exist with energy less than or equal to any chosen value.
This means that topological types of knots can be "ordered" in terms of their
energy. There is a natural numerical scale of complexity for knots, ranging
from simple knots at the low energy end to more complicated ones higher up.
 |
| The Alexander polynomial cannot prove this is knotted, but the Jones polynomial can. |
What are the simplest knots? In the most recent issue of the
Bulletin of the American Mathematical Society, a team of four topologists
- Steve Bryson of NASA's Ames Research
Center in California, Michael Freedman and Zhenghan Wang of the University
of California at San Diego, and Zheng-Xu He of Princeton University- prove
that the simplest knots are exactly what you would expect. They are "round
circles"- that is, circles in the everyday sense. Topologists, whose "circles"
are usually bent and twisted, have to append an adjective to remind themselves
when, as in this case, they are not.
The energy of a round circle is 4, and all other closed loops
have higher energy. Any loop with energy less than
6p + 4 is topologically unknotted - it is a bent
circle. More generally, a knot with c crossings in some two-dimensional
picture has energy at least 2pc + 4, though
this bound is probably not the best possible, as the lowest known energy
for an overhand knot is about 74. The number of topologically distinct knots
of energy E is at most (0.264) x (1.658)E .
The key idea behind their results is a proof that the energy
of a knot is unchanged by a
"Möbius transformation". This is a
special way to deform space, with the pleasant property that it transforms
circles either to circles or to straight lines. It is easy to see that the
energy of a straight line is zero, and any curve of zero energy is straight.
Applying a Möbius transformation leads
to a similar statement about round circles, but now the appropriate energy
level turns out to be 4, not zero.
The Alexander polynomial was pure mathematics, invented for
its own sake. The Jones polynomial arose accidentally from sophisticated
modern mathematical physics. But the energy invariant came direct from classical
physics. Mathematics is a universal language and it grabs its ideas wherever
it finds them. All's fair in love and knot theory.
[See also World20]
