

by Ian Stewart
Knots, Links and Videotape
I've popped the popcorn, Charlotte's brought along the soda-did you manage
to rent the video?" Boris asked.
"Of course I did," Alison replied.
"Exterminator 4. "Oh, that Ernie Scrambledegger," Charlotte sighed. Boris
put the tape on. The screen showed a pattern of irregular white lines, and
then the title sequence came up. They stared at the screen. "Uh- maybe it's
an ad," said Alison hopefully.
"I don't think so," Boris said.
"Alison, what the devil is Not Knot?"
"Whatever it is," said Charlotte in menacing tones, "it certainly isn't
Exterminator 4. Alison, did you forget your glasses again?"
"Well, there was a bit of a mix-up at the checkout-"
"Hold it, guys," Boris said. "The video store's closed now. We'll just have
to make do with whatever it is that Alison got by mistake."
On the screen a mass of multicolored wormlike tubes writhed around like a
creature in its last death throes.
"Aliens," said Charlotte firmly. "Okay, I'll settle for aliens."
"I don't think so," Alison said. "In fact, I'm pretty sure I recognize this.
It's a math video produced by the Geometry Center at the University of
Minnesota."
"A math video?" said Boris in horror.
"Well, we do live in the age of math communicathionth," Charlotte lisped.
"They got a big research grant to set the center up; this is just one of
the things they've done. Hey, the graphics are good. Look at those transparent
boxes. Alison, what's it all about?"
"Some amazing discoveries about the topology of knots," Alison said. "Topology?"
asked Boris, at the same time as Charlotte asked,
"Knots?"
"Um. Imagine tying a knot in a length of tubing and fusing the ends together
so that the knot can't escape. The question is, Can you recognize when two
such knots are equivalent? That is, can you deform one of them into the other
by bending or twisting the surrounding space, without cutting or tearing
it?"
"How do you tear Space?" Charlotte asked. "Or bend it?"
"Imagine it's filled with some kind of very soft, stretchy, squashy Jell-O,
and bend or tear that."
"And this is math? Squashy Jell-O?"
"Not only is the universe stranger than we know," Alison said, "but it is
stranger than we can know. Math especially. Be thankful we're only filling
space with Jell-O."
 |
The Borromean rings |
The screen changed to show three linked rings [see illustration on this page].
"That's a link," Alison said. "like a knot, but with more tubes. Those are
the Borromean rings, which are famous because no two of them are linked,
but all three are.I mean, if you cut any one of them, the whole thing falls
apart, but if you don't, it hangs together."
"Oh."
They watched for a while.
"What's this bit about?"
"They're showing you that if you forget about the knotted tubes and just
look at the spaces outside them-their complements, that's the word-then
inequivalent knots have inequivalent complements." Charlotte thought for
a moment.
"Isn't that obvious? If I follow you correctly, the complement is like the
whole of space filled with Jell-O but with a tunnel burrowed through it where
the knotted tube would be. If you can bend the space outside one knot to
look like the space outside the other, doesn't the knot kind of get carried
along?"
"Yes, but it might get kind of twisted up, I suppose," Alison said. "Anyway,
it can't be obvious, because the same statement is false for links. You can
find links whose outsides are the same but whose insides are different [see
box on opposite page].
Inequivalent Links with Equivalent Complements The two links at the top are inequivalent. In this topologically equivalent representation (bottom), one link has been stretched to create a thick cylindrical tube. Cut the right-hand picture across the top of the cylinder (dotted line). If you rotate the links to untwist them and then reattach them, you get the left-hand picture. This proves that the complements are equivalent. But the left-hand link falls apart completely if you cut the cylindrical tube, whereas the right-hand link does not, so the two links are inequivalent. |
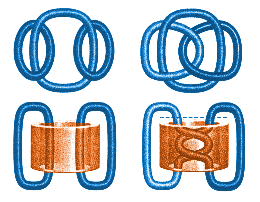 |
"The argument seems to involve cutting things," Boris protested. "I thought
you weren't allowed to cut the space."
"Okay, so I lied. You can cut it, provided you glue it back together later.
Just as it was."
"But then you can untie a knot," Boris protested. "Cut the tube, undo the
knot, then glue it back."
"Which is why, Boris, dear, you have to deform the space around the knot
and not just the knot," said Charlotte, who was finding the video more to
her taste than she'd expected. "Which in turn is why it's called Not Knot"
"Thanks, Charlotte," Boris said. "Hmm, it's getting more complicated now."
"Yes. It's leading up to the recent discovery that knot complements have
a natural geometric structure, which you can use to tell the difference between
inequivalent knots. The interesting thing is that it's
non-Euclidean geometry that shows up," Alison
explained.
"You're telling me there's more than one kind of geometry?" Charlotte asked.
"There are lots of different kinds of geometry-ordinary Euclidean geometry
is just one of them. The main difference in non- Euclidean geometry is that
parallel lines behave in funny ways and may not exist at all. You can visualize
two-dimensional non-Euclidean geometry by replacing the plane with curved
surfaces, like spheres or saddle shapes, and drawing the lines and stuff
on those. But for knot complements, you need to think about three-dimensional
curved spaces, and that's hard. So what the video does is fly you around
inside such a space and show you what it would look like."
Boris looked at the screen, where tiny cars were chasing one another around
a cone. "Flies? With a car?"
"The flying bit comes later. Here they're showing you how to make non- Euclidean
geometries by kind of cutting a slice out of ordinary space and gluing the
edges together. Just as you can make a cone from a circular piece of paper
with a pie-shaped slice cut out. Only you just have to imagine what the result
of such a gluing process would be. The idea is that whenever you draw a line
that hits an edge of the slice, you immediately transfer to the corresponding
place on the other edge of the slice and carry on drawing. That kind of bends
the lines, even though each bit of them is straight-so not only do you get
funny effects with parallel lines but also a 'straight' line that can bend
around and cross itself."
Boris looked puzzled. "Alison, how can a straight line bend?"
"When I say 'straight' I mean the line that covers the shortest distance.
When the space has a non-Euclidean geometry, straight lines don't always
look straight to us-looking in from the outside. But if there were light
rays that followed the shortest paths, then to a creature living in the space
the lines would look straight".
"Another way to create non-Euclidean geometries is to use mirrors," Alison
went on.
"Like a kaleidoscope. The mirrors have the same effect, changing the direction
of light rays. For instance, imagine you are inside a cubical room whose
floor, walls and ceilings are all mirrors. What do you see?"
Reflective Musician Musician Mike Oldfield borrowed the ideas of the geometry of "a cubicle room of mirrors" in his "Guilty" single cover.In other stage performances he has used the art of Escher , which also exploits mathematical geometries to produce fascinating pictures. |
 |
Charlotte thought for a moment. "Lots of copies of me."
"Yes. The images of the cube in the mirrors would tile space, and in whatever
direction you looked, you'd see yourself. Well, a reflection of yourself.
But mathematically we can pretend that each reflection really is you, the
same you. That has the effect of 'gluing' opposite mirrors together, just
as we glued the edges of the cone. But now you get a three-dimensional space
with weird geometry. For instance, the straight line starting at your forehead
and traveling horizontally forward eventually runs back into your
forehead."
"So straight lines can make U-turns?"
"Yeah. But they stay straight, which is perfectly natural if you happen to
be a creature that lives in a knot complement. Now, you can set up a different
kind of mirror-mathematical, not physical-that turns things upside down as
well as reflecting them. Call them inverting mirrors, okay? If the walls
of the cube were inverting mirrors, you'd see lots of copies of yourself,
but some of them would be upside down [see top illustration on next page].
This particular geometry, a cube with inverting mirrors for faces, is one
possible geometry for the complement of the Borromean rings. The video explains
why in detail, but I'll try to summarize. An inverting mirror-in the sense
we've just been talking about--is a place where space wraps around it self
in strange ways. A kind of space warp. With me so far?"
"Hanging on by my toenails."
"Now, take the three separate tubes that make up the Borromean rings and
stretch each tube until it gets very long and thin, with its edges straight
for most of their length. Like an athletics stadium, only with the straight
parts of the track being much longer. If you do it right, you can get a pair
of parallel tubes that runs north-south, say; another pair that runs east-west;
and a third pair that runs up-down. Plus extra U- shaped pieces joining them
at each end, which we'll push away to infinity so they don't matter."
"Gotcha."
"You can find a similar arrangement of lines on a cube. On the floor and
ceiling, run a line down the middle, going north-south. On two of the walls,
draw horizontal lines running east- west. On the remaining walls, run vertical
lines up the middle. The important thing is that those lines stay fixed when
you 'reflect' them in inverting mirrors on the cube's faces. That lets you
relate the corresponding geometry to the complement of the Borromean rings.
It means that when you perform all the inverting reflections, the images
of the lines on the cubes fit together so that they stretch away to infinity,
just as the Borromean rings do after we push the U-bends off to infinity.
And that means that the space around them-the funny geometry with lots of
copies, some upside down-is just like the space around the Borromean rings.
"I'll believe you," Charlotte said.
"Okay-or else watch the video again, carefully."
"The night is young yet," Boris said. He stopped, spellbound. "Hey, this
bit is really neat. It's like being inside some kind of cage and moving around
through the bars."
"This is the flying part," Alison explained. "The bars are the edges of
dodecahedrons. Well, really they're all the same dodecahedron, because you
have to imagine everything glued together as the faces of the cube were.
But if you lived inside such a space, you'd see multiple copies of everything,
like the picture with the inverting mirrors. It's another geometry you can
get from the complement of the Borromean rings by using a different kind
of 'mirror.' Regular mirrors on the faces of a cube produce cubic images
that tile space, and similarly non-Euclidean mirrors on the faces of a
dodecahedron produce dodecahedral images that tile non-Euclidean space. The
edges are at right angles, so you can fit four of them together, and that's
why they tile."
 |
Inverted reflections in all directions: one possible geometry (or the compliment of the Borromean rings |
 |
A non-Euclidean tiling of space by regular dodecahedrons |
"Hold it," Charlotte interjected. "A dodecahedron I understand-it's a solid
with 12 pentagonal faces."
"Right."
"But they don't meet at right angles."
"Not in Euclidean space, no. But this space is non-Euclidean-curved, if you
wish. Bent just enough to make them into right angles."
"I guess I see that."
"The video really does let you see it. You fly through it; you can see what
it looks like, really feel the weird curvature effects that come from
non-Euclidean geometry [see bottom illustration on this page]. It's quite
strange and beautiful."
"Yeah," Boris said. "It kinda gets to you after a while. I could imagine
living in a space like this. It's roomy."
"How do you mean?"
"Well, flying around it like this you can see that surrounding each dodecahedral
tile there are a lot more other tiles than you could fit into ordinary Euclidean
space. The amount of space gets bigger than you'd expect as you move outward."
"That's called negative curvature. It shows you're in what's called hyperbolic
space, one particular kind of non-Euclidean geometry. And that's the central
point of the video. According to a recent discovery made by
William P. Thurston of the Mathematical Sciences
Research Institute, nearly all knot and link complements have a natural
hyperbolic geometry. There are a few exceptions, but they're all known. And
you can use the geometric structure to tell all of the others apart. That
is, inequivalent knots or links have different geometric structures. It's
an amazing connection-I dare not say 'link'-between the flexible geometry
of topology and the rigid geometry of non-Euclidean spaces. So now a very
old-fashioned branch of math-non- Euclidean geometry-is back in vogue."
"Great," said Charlotte, rewinding the tape. "But what would be really great
is if they hired Ernie Scrambledegger to star in the sequel."
"The Geometry Center got a big grant," Alison said. "But not that big."
[See also World20]
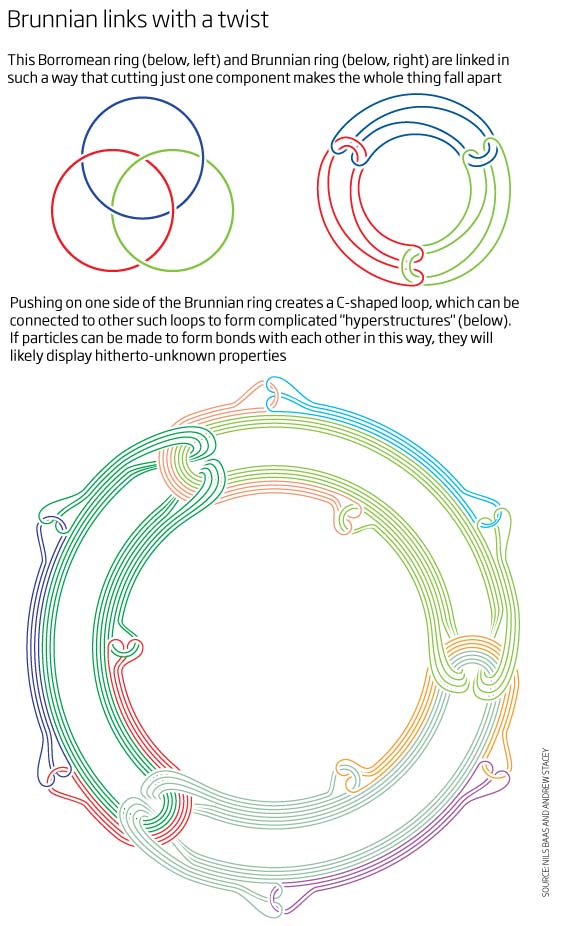 |
Make way for mathematical matter 05 January 2011 by Michael Brooks Magazine issue 2794. Subscribe and save Editorial: "The deep value of mathematics" WE ALREADY have solid, liquid, gas, plasma and Bose-Einstein condensate. Now it seems we may be on the verge of discovering a whole host of new forms of matter - all based on mathematics. Nils Baas, a mathematician at the Norwegian University of Science and Technology in Trondheim, has unearthed a plethora of possibilities for the way the components of matter can link together. He made the discoveries while researching the field of topology - the study of the properties that objects share because of their shape. It is particularly concerned with the various shapes that can be formed while squashing and bending an object. A ring doughnut and a teacup share the same topology, for example: it is possible to squish the doughnut into a teacup shape without doing away with the hole, as it becomes the hole in the handle. Baas was studying "Brunnian rings" - collections of rings that are linked together but can all be separated if only one ring is cut. Borromean rings are the most famous example (see illustration). Baas has shown that many more linkings are possible: not only are there Brunnian links of four or more components, there are also sets of Brunnian links which are themselves linked together in a Brunnian fashion to create what Baas calls "hyperstructures" (arxiv.org/abs/1012.2698). In 1970, Vitaly Efimov, now at the University of Washington in Seattle, predicted that the topology of the Borromean rings would be reflected in nature as a hitherto-undiscovered form of binding between three particles. In the last five years, it has been shown that some of these links can indeed occur in physical systems. In 2006, researchers found this "Efimov state" in a gas of ultra-cold caesium atoms: each atom had a single link to one of the others, but picking up one moved all three (Nature, DOI: 10.1038/nature04626).
|
| Then, in 2010, Japanese researchers found Borromean rings in
the bonds between atomic nuclei (Physical Review Letters, vol 104, p 062701).
"These structures seem to act as a recipe for what you can construct in the
real world," Baas says.
But Baas's more complicated hyperstructures have radically different topologies from anything yet seen in nature. If groups of particles can be made to bond in this way, they would create matter with previously unseen properties, Baas reckons. "When you go to a higher level, something completely new happens mathematically - and I would suspect it does in the real world too," he says. Baas has teamed up with Ned Seeman of New York University in New York City to figure out how to build the hyperstructures. "Mathematics seems to be a pretty good predictor of reality," says Seeman, who synthesised Borromean rings using DNA strands in 1997. "I have every suspicion that they'll work out." Baas has plenty of other avenues to explore, too, including a new inroad into the fundamentals of quantum theory. Particles that interact can become curiously synchronised, even when separated, in a quantum process called entanglement. If the particles start out linked together in complex Brunnian ways, they might be able to affect each other even when separated, he says, providing new ways to create the spooky-action-at-a-distance connections like those observed in entangled systems. "Once [these links] have been pointed out from topology, then we can go back and look for them in the Schrödinger equation" that describes the mathematics of quantum theory, says Baas. From there, it might be possible to create new quantum states in the lab. This in turn might provide new ways to build super-powerful quantum computers, which manipulate information carried in the quantum states of particles. Such quantum information can be in many states at once, so quantum computers can carry out enormous numbers of calculations simultaneously. The original version of this story incorrectly stated that each of the three Borromean rings is threaded through only one other. That has since been fixed. |
|
Further Reading
NOT KNOT. Video. Directed by Charlie Gunn and Delle Maxwell.
Supplement written by David Epstein and Charlie Gunn. Produced by Geometry
Center, University of Minnesota, 1991. Distributed by A K Peters, Wellesley,
Mass. Telephone: (617)239-2210. |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
Scientific American January 1994 File Info: Created 20/6/2000 Updated 24/3/2014 Page Address: http://leebor2.100webspace.net/Zymic/notknot.html