Maps that shape the
world
|
|
| "We wanted the computer to do absolutely as much as possible unassisted,but in no way violating the integrity of the aesthetics with which a human would have done it" - Mitchell Feigenbaum |
Like a huge piece of orange peel that refuses to be flattened without
tearing at the edges, the globe cannot be forced into two dimensions without
distortion. But that distortion can now be minimised
Ian Mundell
IN 1940 the US Air Force estimated that less than 10 per cent
of the world was mapped in enough detail to make
the charts its pilots needed. Aerial surveying during and after the Second
World War filled most of the gaps, and in the past two decades there has
been a flood of data from Earth observation satellites. But modern atlases
are still based on survey data obtained before the advent of satellite
photography. Until now, cartographers have not used the combination of
new mathematics and computing power needed to
exploit this mass of data.
It has taken an outsider to change all this. The chaos
theorist
Mitchell Feigenbaum, who is professor
of mathematics and physics at the Rockefeller University in New York, was
brought in by the map publisher Hammond as an adviser on how best to computerise
the production of a new atlas lie abandoned the conventional approach to
computerised map making, which uses computers primarily to strip the labels
off existing maps and add new ones. Instead, he set out to devise a complex
program capable of producing the most accurate maps that could be made from
the data available.
The publisher claims that the resulting atlas is the first to have been produced
entirely from a computerised database which holds digitised information on
billions of reference points from the latest satellite pictures of the Earth.
Not only has the map labelling been computerised, so also has the redrawing
of maps at different scales. The real revolution, though, lies in the continental
maps. Drawn with levels of distortion lower than ever before, their mapping
is based on an idea dating back to the early part of this century, now made
practicable by computers and modern mathematics. Little of this is noticeable
to the untrained eye, since much of what the computers have done automates
the skills of the expert cartographer. "We wanted the computer to do absolutely
as much as possible unassisted, but in no way violating the integrity of
the aesthetics with which a human would have done it," says Feigenbaum.
Flattening the globe
Cartography is dogged by the problem of how to transfer distances on the
curved surface of the Earth to the flat surface of a map. Methods for doing
this are called projections, a term derived from geometric approaches that
take points on the spherical Earth and project them onto another three-
dimensional surface which can then be flattened into a map. Cylindrical
projections, for example, represent lines of latitude as horizontal lines
on a cylinder, and those of longitude as vertical lines. The cylinder is
then cut along its length and unrolled to give a flat map.
The choice of projection depends partly on the purpose of the map and partly
on the size of the area the cartographer wants to depict. No flat map can
show accurately all three crucial attributes of the area being mapped: the
distance between points, the area within a given boundary, and the shape
of a given area. For atlases, where a broad representation of the Earth's
surface is required rather than precision in any one attribute, the main
inaccuracies are distortion of shape or distance. On large-scale maps the
difference between curved distance and flat distance is negligible and can
be ignored. But as the area being mapped grows, so does the potential for
distortion -areas even a few tens of miles across must take account of the
Earth's curvature. The cartographer has to decide where distortions will
cause least damage, given the map's purpose. This is where the choice of
projection is crucial.
Some projections aim to produce maps in which the angles, and therefore the
shapes on the paper, are as close as possible to those on the ground. With
these so-called conformal maps, the distortion occurs in the distances
between points and in the areas within boundaries. The projection developed
in 569 by Gerardus Mercator is a cylindrical conformal projection. It gives
considerable distortion at high latitudes but has the advantage that compass
bearings are consistent at all points on the map. Any path along a particular
compass direction therefore appears as a straight line on a Mercator projection,
which is why it is still the basis of most charts used for navigation. There
is, however, no conformal way to show the entire surface of the Earth without
infinitely distorting some areas.
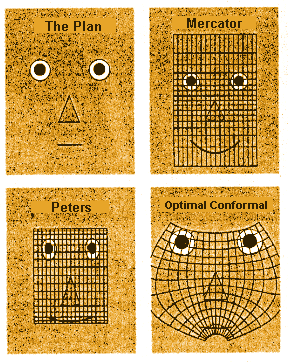 |
| Distorted world-view: the optimal conformal projection represents the plan more faithfully than either the Mercator or Peters projections |
Other projections aim to show surface areas in correct proportion
to each other. These "equal-area" maps, such as the Peters projection, became
popular in the 1980s because of their attribute of depicting country sizes
in true proportion- unlike the Mercator projection, which minimises the areas
of most Third World countries, as they tend to be near the equator, and maximises
areas near the poles. But the price of this is a huge distortion of shape.
Best of all possible worlds
On the basis that the best map is that with the least distortion of any sort,
Feigenbaum asserts that the whole idea of equal area maps may be flawed.
"It is very difficult to judge whether areas are equal," he argues. "The
only things that human eyes can judge is linear distances."
Conformal projections have been used throughout the new Hammond atlas. Some
are familiar, such as the Lambert conic conformal projection. This projects
surface detail onto a truncated cone arranged to intersect with the Earth's
surface along two circles of longitude that become the top and bottom of
the map. The atlas uses the Lambert projection for the large-scale country
maps, while the global maps have been made using the Robinson projection,
a compromise between conformal and equal-shape maps that attempts to balance
all the distortions. However, the continental maps are more revolutionary,
since no single projection has been used.
They rely on the fact that for any chosen area on the surface of the Earth
there is a projection which produces the best possible conformal map. Feigenbaum
therefore designed a computer program that takes data about the boundary
around an area to be mapped and calculates what the "optimal conformal
projection" (the projection that minimises inaccuracies) will be. The map
of South America, for example, is better than 98 per cent accurate; other
atlases score around 95 per cent. Feigenbaum's maps of regular shapes such
as Australia have a very small distortion, while Africa and North America
may be distorted by 3 per cent. "These maps are uniformly twice as good as
any projection that has ever been made before," says Feigenbaum.
The idea of the optimal conformal projection was first conjectured by the
Russian mathematician Pafnutii Lvovich Tchebychev in the middle of the last
century. However, it is only recent developments in computing that have allowed
Tchebychev's theory to be put into practice.
In essence, the method is this: the relationship between a distance on the
Earth's surface and a distance on the map is known as the scale factor. On
a globe, the scale factor is constant throughout. This is not the case on
a map because of the distortions caused when you flatten the curved surface:
on any map the scale factor varies from point to point.
"You want to find that analytic function which produces a map for which the
scale factor is as constant as possible," explains Feigenbaum. "The solution
to that problem turns out to be that the scale factor must be constant on
the boundary around the area you are mapping." Calculating this constant
scale factor provides information that can be fed into a set formula. Solving
this tells the computer how to manipulate data representing all the points
within the map so that the distortion across the whole map is as small as
possible.
The conformal projection selected by this method is, by definition, the best
possible for the area in question. Careful selection of the area can reduce
the distortion, but beyond that, the only improvement would be to show that
some other system could perform better than conformal projection. "I'm sceptical
that is possible," says Feigenbaum. "But I don't know how to prove that."
The labelling method designed by Feigenbaum uses a computer to tackle the
problem, much in the way a human would. Previous computerisations have perversely
chosen rule-based methods that restrict a label to a limited number of positions
around the point it refers to. Feigenbaum treats the space around a point
as a continuum, and takes into account the space available in the whole of
the mapped area. The system is based on simple electrostatics: the labels
are made to behave as though they are charged entities moving in a field
which makes them appear to "flow" along parallels in the part of the world
being mapped. Other rules maintain an acceptable association between point
and label, and prevent overlap. "It's a molecular dynamical calculation.
Every one of these things is busily buzzing around, seeking some decent
equilibrium."
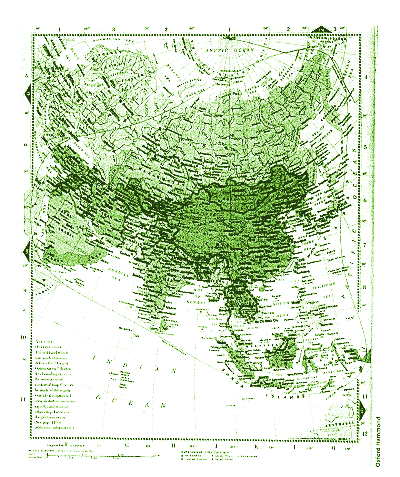 |
| Doing the continental: optical conformal maps in the new Hammond atlas are twice as accurate as other continental maps. The red line marks the boundary of the map, beyond which distortion occurs |
The fractal factor
Another human skill automated for the new atlas comes into play when changing
the scales. The data used to produce the maps is
fractal: the closer you get to it the more structure
emerges. This makes for problems when scaling a map up or down because it
is not possible simply to magnify or reduce the existing boundaries. Going
from a detailed large-scale map to a smaller scale, a smooth line of fractal
data will turn into a highly irregular broad line. "A cartographer would
see this more precise data and then, by his own training, figure out a much
simpler curve to cast through it that would have the right integrity at that
much smaller scale," explains Feigenbaum.
The computer does something similar. It examines the detailed fractal data
and analyses the hierarchy to determine what the data represent and which
points have greatest significance. On a small-scale map of the Scandinavian
coast, for instance, it is not good enough simply to smooth over the smaller
fiords. Any town at the head of one of these fiords would appear land-locked
on the map. But if the computer program contains the instruction that any
coastal town must appear as such on the smaller scale, it can draw a suitably
sinuous line.
Only one part of the new atlas is not automated. The relief maps are produced
by photographing handmade relief models. Relief data for the whole world
are not good enough for automation, and no on is sure how best to treat the
surface of the Earth mathematically. A mountain range is neither sufficiently
smooth for conventional surface analysis, nor is it entirely fractal. "The
whole geometry of these mountains is immensely interesting," says Feigenbaum.
"At the moment we do not own any of the mathematics that allows us to understand
surfaces for which the normal is varying in a more peculiar way-that perhaps
have partial planes and then suddenly change."
Feigenbaum sees his next challenge as solving this remaining problem. This,
together with further developments of the satellite database will mean maps
could look very different in the 21st century. "There is the potential,"
says Feigenbaum, "to make archival, truly wonderful images of the Earth."
Links Atlas | Maps | MAPS | Antique maps | Yale library | Mercator | Streetmap | The Beauty of Maps | Old maps | Oddens | |
