
The Mathematical Experience |
by Philip J Davis & Reuben Hersh |
 |
The role of astrology in the development of mathematics, physics,
technology and medicine has been both misrepresented and down played;contemporary
scholarship has been restoring proper perspective to this activity.We are
dealing here with a prescience and a failed science.It can be called
a false or pseudoscience only insofar as it is practiced with conscious
deception.
The roots of astrology can be found in Babylonia of the fourth century BC,if
not earlier. Astrology and divination were widespread in the East and can
be found today as an integral part of life in various portions of the East.In
the West,one sees remnants of astrology as a kind of pop culture in the
numerology of the newspaper,computer horoscopes,and zodiac books.
Astrology has waxed and waned and waxed again.At times it has been denounced
as superstition - naturally.It has played an official role in governments
and religious establishments,it has been reviled and proscribed,it has been
thought immoral and iniquitous;it was considered heretical,for does it
not contradict
free will? It has been tolerated
and winked at.It has been used as a teaser,as when the famous mathematician
and physician Cardano cast a horoscope of Jesus.When in the 1500s it was
pursued honestly as a science,it could not help but influence the course
of scientific discovery.
Astrology proceeds from the belief that the celestial bodies affect the affairs
of men.The position of the man on the moon,and of the planets as they make
their way across the backdrop of zodiacal constellations [which are an optical
illusion -LB] ,are said to influence the fate of individuals,of kings and
rulers,and of nations in a vital way.
That there is something to this,no one can deny.Does not the sun energize
our life? Do not changes in its radiation pattern affect
the weather,and the radio reception? Do not the
sun and the moon together control the tides?
Does not,according to a modern cosmologist,the existence of matter at the
furthest reaches of the universe create the gravity that keeps our tennis
balls from flying away? What a grand conception of the universe this is,uniting
the immense with the miniscule,the near with the far! This is the Grand Plan
and the problem now becomes,how can we read this plan for our own purposes?
Among the classic forms of astrological practice we find genethlialogy,catarthic
astrology, and interrogatory astrology,all three interrelated.Genethlialogy
asserts that celestial omens at the moment of one's birth affect the course
of one's life.To predict this course one needs to know the exact moment and
place of birth.One must calculate where the planets were and calculate certain
relationships between them such as conjunctions and oppositions.
Catarthic astrology asserts that any act is influenced by the celestial omens
at the moment of the inception of the act.Therefore,from a knowledge of the
future position of the planets,one can forecast auspicious dates for the
occurrence of important events.
Interrogatory astrology invites questions of all sorts.Where did I lose my
wallet? Should I marry such a one? It asserts that the moment of interrogation
affects the correct answer.Thus does astrology give answers in a world full
of bitter problems,where advice is rare and of doubtful quality.
[Knowledge of the future of any kind is prohibited by modern physics via
mathematics from Heisenberg's Uncertainty
Principle,which renders the future unknowable at its very core,and therefore
any type of prediction based on the planets is false-LB]
To practise astrology in its intensive forms,one had to know astronomy,
mathematics, medicine and much besides,for its methods (algorithms) were
elaborate.When a patient came in with a complaint,the first thing to do was
to cast his nativity.This would be based on information as exact as one had
about the time of his birth.Almanacs were available which would tell the
practitioner about the state of the heavens at the moment of birth.How did
one know the moment of birth? This,remember,was in a period in which the
average person could neither read nor write nor reckon,when a knowledge of
the number of miles from London to Canterbury was given as one of the great
reasons for learning arithmetic.But given a nativity of even an approximate
sort,the astrologer - mathematician - physician would proceed to examine
the patient's symptoms (in particular the color of his urine),and then come
up with a prescription.This was the ten-dollar job.
Naturally,when the patient was a member of the nobility or the clergy or
when the patient was the astrologer himself,first-order accuracy was thought
insufficient. An exact horoscope was necessary and this,of course,would cost
a hundred dollars.This created the necessity for accurate tables of planetary
positions,instruments whose accuracy exceeded that of the run-of-the-mill
astrolabe or transit,accurate clocks,convenient and accurate modes of
mathematical computation.Thus,to be a physician in,say,the thirteenth century,one
had, ideally,also to be a herbalist,and alchemist,a mathematician,an
astronomer,and a maker of scientific instruments.The pursuit of accurate
knowledge of time and position leads through Brahe,Kepler,Galileo and Newton
to contemporary physics and mathematics.

Astrologers must have chalked up quite a few successes.Even tossing a coin
is often a useful device for instituting [Ref: Davis & Hersh p163
{The Coin of Tyche}] policy and by the law
of averages should be right every now and again.So one hears of the spectacular
job done by
John
Dee for the young Queen Elizabeth.Dee,asked to provide an auspicious
date for the coronation of Elizabeth I,worked his science and came up with
the date that led to England's dominance of the world for more than three
hundred years.
[It makes no difference when she was crowned.England would have dominated
regardless of what date she became queen,even if it didn't the date chosen
by Dee makes no odds to the outcome-LB]
But in the long run,though astrology was a prescience,and though many of
its practitioners pursued it in the spirit of modern scientific enquiry,it
was a failure,one of many failed theories having a mathematical core.It provided
a wrong model of reality and this led to its decline and to its
intellectual trivialization.
"We who are heirs to three centuries of science," writes Sir
Kenneth Clark in his marvellous Landscape into Art,"can hardly imagine
a state of mind in which all material objects were regarded as symbols of
spiritual truths or episodes in sacred history. Yet, unless we make this
effort of imagination, mediaeval art is largely incomprehensible." We who
are heirs to three recent centuries of scientific development can hardly
imagine a state of mind in which many mathematical objects were regarded
as symbols of spiritual truths or episodes in sacred history. Yet, unless
we make this effort of imagination, a fraction of the history of mathematics
is incomprehensible.
Read how Plutarch (40 A.D.-120 A.D.), in describing the Isis cult of Egypt,
blends sacred history and mathematical theorems.
The Egyptians relate that the death of Osiris occurred on the
seventeenth (of the month), when the full moon is most obviously waning.
Therefore the Pythagoreans call this day the "barricading" and they entirely
abominate this number. For the number seventeen, intervening between the
square number sixteen and the rectangular number eighteen, two numbers which
alone of plane numbers have their perimeters equal to the areas enclosed
by them,* bars, discretes, and separates them from one another, being divided
into unequal parts in the ratio of nine to eight. The number of twenty-eight
years is said by some to have been the extent of the life of Osiris, by others
of his reign; for such is the number of the moon's illuminations and in so
many days does it revolve through its own cycle. When they cut the wood in
the so-called burials of Osiris, they prepare a crescent-shaped chest because
the moon, whenever it approaches the sun, becomes crescent-shaped and suffers
eclipse. The dismemberment of Osiris into fourteen parts is interpreted in
relation to the days in which the planet wanes after the full moon until
a new moon occurs. "
* This is a nice theorem. Prove it.
All is number," said Pythagoras, and number mysticism takes
this dictum fairly literally. The universe in all its aspects is governed
by number and by the idiosyncrasies of number. Three is the trinity, and
six is the perfect number, and 137 was the fine-structure constant
of Sir Arthur Eddington, who was a number mystic and a distinguished
physicist.
In the year 1240, the most triumphal year in the reign of Frederick II of
Sicily, western Europe was beset by rumors of a great king in the far East
who ruled over a vast kingdom and who was making his way slowly and relentlessly
westward. One Islamic kingdom after another had fallen to his sword. Some
Christians interpreted the news as presaging the arrival of the legendary
Prester John who would unite with the kings of the West in Jerusalem and
seal the doom of the Islamic religion. The Jews of Europe, for reasons to
be explained shortly, held this Eastern monarch to be King Messiah, the scion
of David, and proposed going forth to meet him in joy and celebration. Other
Christians, while agreeing with the messianic interpretation, held that Frederick
himself, stupor et dominus mundi, the marvel and master of the world, one
of the most remarkable intellects ever to sit on a royal throne, was the
promised Messiah.
Now on what basis was it concluded that the Messiah was arriving?
Simply that the year 1240 in the Christian calendar corresponded to the year
5000 in the Jewish calendar and that, according to some theories, the Messiah
was to appear at the beginning of the sixth millennium. Here we have a
piece of number mysticism of a sort which is incredible to the modern mind.
(At this point, we should inform our curious reader that the eastern king
was neither Prester John nor the Messiah but Batu, son of Genghis Khan and
the founder of the Golden Horde, who slaughtered his way up to Liegnitz in
Silesia.)
But the sacred merges imperceptibly with the practical. Mathematics,
asserted Henry Cornelius Agrippa, a popular philosophical magician of
the sixteenth century, is absolutely necessary for
magic, "for everything which is done through natural
virtue is governed by number, weight and measure. When a magician follows
natural philosophy and mathematics and knows the middle sciences which come
from them-arithmetic, music, geometry, optics, astronomy, mechanics-he can
do marvelous things."*
(* Frances Yates, Giordano Bruno and the Hermetic Tradition.)
One of the ways in which number mysticism works itself out is through the
art of gematria (the
word itself is derived from "geometry"). Gematria is based on the fact
that the classic alphabets of Latin, Greek, and Hebrew normally have numerical
equivalents. In its simpler form, gematria equates words with equivalent
numbers and interprets the verbal equivalents. Here is an example from the
period of Frederick II. The name "Innocentius Papa" (Pope Innocent IV) has
the numerical equivalent 666. This is the
"Number of the Beast" of Revelations 13:18 and hence Innocent equals the
Antichrist. (Frederick was violently antipope.)
What sort of nonsense and intellectual trash is this, one wonders,
particularly when one realizes that public policy may have been based upon
such reasoning. One hopes that contemporary political reasoning is based
on firmer stuff. Yet this kind of reasoning, this riding rough-shod with
numbers, may have fostered number skills and interests that far outweighed
the damage done.
To the medieval mind, a number, particularly if it were
a sacred number, was a manifestation of divine and spiritual order. It
could be turned into an aesthetic principle.
As an example, we mention a recent analysis by Horn of a master plan for
a monastic settlement drawn up in Aachen in 816. This is the so-called "Plan
of Saint Gall." Horn finds that the designing architect kept the sacred numbers
three, four, seven, ten, twelve, and forty in his mind and worked with them
repeatedly. We shall bypass the credentials or the certification of the holiness
of these specific numbers and pass to the architectural detail.
In the plan, there are three major areas-east, central, and west. There are
three building sites, three cloisters, three bake and brew houses, three
bathhouses, three medical installations, three walled gardens, three poultry
pens, and three milling installations.
There are four circular structures, four altars in the transept and four
in each aisle, and four pieces of liturgical furniture in the nave. There
are four rows of plantings. Four also plays a role in the basic modules of
the layout.
Seven buildings form the core of the monastic settlement. There are seven
steps which raise the presbytery above the crossing, seven desks for the
scribes in the scriptorium. There are seventy- seven beds in the monks'
dormitory. There are seven liturgical stations in the axis of the church.
There are seventeen (10 + 7) altars in the whole of the church and twenty-one
(3 x 7) altars in the whole of the plan.
We shall not pursue Horn's extensive catalogue of sacred numbers
through forty. If the skeptic finds that these occurrences are accidental,
or merely evidence that all numbers can be decomposed by sums or products
into a list of sacred numbers as in the prime decomposition theorem,
or Goldbach's conjecture
(see Chapter 5), let him work with
the master plan of his local Howard Johnson's motel and discern what sacred
plan it conforms to.
Further Readings.
See Bibliography J. Griffiths; W. Horn; F. Kantorowicz; F.
Yates
|
| Giordano Bruno 1548-1600 |
 |
| Hermetic Figures From Giordano Bruno Articuli centum et sexaginta adversus huius tempestatis mathematicos atque philosophos,Prague,1588 (p313 ff) |
The dream of philosophic magic (to be distinguished from conjurer's
magic) has persisted for millennia. One of the fundamental assumptions of
this magic is that spiritual forces in the universe may be induced to
enter in and influence the material forces. The spiritual is celestial,
the material is earthly. Earthly forms are often represented as geometrical
figures and as such are thought to be aspects of the pure celestial forms.
By proper representation and arrangement, the material figure induces a kind
of sympathetic resonance with its celestial counterpart and, as a result,
the figure is endowed with the potency of a talisman. This potency
is then applied to strictly practical ends-the curing of illness, the
achievement of business success, destruction of one's enemies, practical
erotics, and many others.
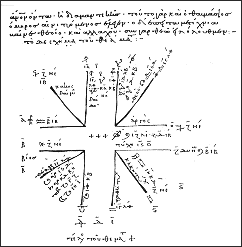
The accompanying illustration shows three pieces of hermetic
geometric art dating from 1588. They have been taken from the book Arliculi
. . . adversus . . . mathematicos atque philosophos written by Giordano Bruno.
Bruno was an ex-Dominician, a brilliant philosopher, and a philosophic
magician.
These figures strike us today as pleasant designs which would make agreeable
tile work. One supposes that the specific arrangements are not arbitrary,
but have been created according to some principle. Many have thought (and
think) they have discovered the keys to the universe.
One should not hold a key in contempt because it opens up only a minor chamber
at the periphery. A fourth hermetic figure is the
magic hieroglyph of John Dee (1564). It
may remind one of the peace symbol of the early 1970s. The mathematical and
magical properties of this symbol are set forth in a book called Monas
Hieroglyphica which explains its construction and its interpretation through
a sequence of "theorems." The reader should compare the theorematic material
here with that of Euclid given in Chapter 5.
Further Readings.
See Bibliography G. Bruno; J. Dee; C. Josten; F. Yates
Mathematics, in an earlier view, is the science of space and
quantity; in a later view, it is the science of pattern and deductive structure.
Since the Greeks, mathematics is also the science of the infinite. Hermann
Weyl speculates that the presence of the infinite in mathematics runs
parallel to religious intuition:
 |
| Hermann Weyl 1885-1955 |
...purely mathematical inquiry in itself, according to the
conviction of many great thinkers, by its special character, its certainty
and stringency, lifts the human mind into closer proximity with the divine
than is attainable through any other medium. Mathematics is the science
of the infinite, its goal the symbolic comprehension of the infinite
with human, that is finite, means. It is the great achievement of the Greeks
to have made the contrast between the finite and the infinite fruitful for
the cognition of reality. Coming from the Orient, the religious intuition
of the infinite, the
apeirsu, takes hold
of the Greek soul. This tension between the finite and the infinite and its
conciliation now become the driving motive of Greek investigation.
Like mathematics, religions express relationships between man
and the universe. Each religion seeks an ideal framework for man's life and
lays down practices aimed at achieving this ideal. It elaborates a theology
which declares the nature of God and the relationship between God and man.
Insofar as mathematics pursues ideal knowledge and studies the relationship
between this ideal and the world as we find it, it has something in common
with religion. If the objects of mathematics are conceptual objects whose
reality lies in the common consciousness of human minds, then these shared
mathematical concepts may constitute the dogma of mathematical belief.
It is the writer's impression that most contemporary mathematicians
and scientists are agnostics, or if they profess to a religious belief, they
keep their science and their religion in two separate boxes. What might
be described as the "conventional scientific" view considers mathematics
the foremost example of a field where reason is supreme, and where emotion
does not enter; where we know with certainty, and know that we know; where
truths of today are truths forever. This view considers religion, by contrast,
a realm of pure belief unaffected by reason. In this view, all religions
are equal because all are equally incapable of verification or
justification.
However, this perceived dichotomy between mathematics and religion,
though now widespread, is not universal; and over the centuries, the interplay
between mathematics and religion has taken various fruitful forms. Religious
considerations have, for instance, spurred some kinds of mathematical creation
and practice. Scholars like A. Seidenberg have sought the origins of counting
and geometry in ancient rituals. The development of the calendar is another
example. To what extent was the development of the calendar influenced and
fostered by a desire to standardize periodic ritual events?
We have also observed in regard to number symbolism and number mysticism,
how religious practice may be affected by mathematics.
At a somewhat deeper level of cultural influence we can see
how notions of mathematical proof have contributed to the development of
theology. The medieval schoolmen looked for rational proofs of theological
theorems, so that points of dogma might be established Q.E.D.
Nicolas of Cusa (1450) believed that the true love of God is amor Dei
intellectualis and that the intellectual act through which the divine
is revealed is mathematics. (The divine is to be reached through many
paths, e.g., through cleanliness, or through uncleanliness as in the case
of the Desert Fathers. Nicolas asserts that the divine is to be reached through
"thinkliness.")
The German romantic epigrammatist Novalis (Friedrich von Hardenberg,
d. 1801) said that "Pure mathematics is religion," because, as later explained
by the choreographer Oskar Schlemmer in 1925, "It is the ultimate, the most
refined and the most delicate." Novalis, who had read quite a bit of contemporary
mathematics, also wrote "Das Leben der Götter ist Mathematik" and "Zur
Mathematik gelangt Man nur durch eine Theophanie."
As further instances of this tendency consider Spinoza's treatment of ethics,
more geometrico, and John Locke's statement
in "An Essay on Human Understanding":
Upon this ground it is that I am bold to think that morality
is capable of demonstration, as well as mathematics: since the precise real
essence of the things moral words stand for may be perfectly known, and so
the congruity and incongruity of the things themselves be certainly discussed;
in which consists perfect knowledge.
Conversely, religious views of the world have posited
mathematics as a paradigm of Divine thought. The nun-playwright Hrosvita
of Gandersheim (980), in her play "Sapientia," after a rather long and
sophisticated discussion of certain facts in the theory of numbers, has Sapientia
say that
this discussion would be unprofitable if it did not lead
us to appreciate the wisdom of our Creator, and the wondrous knowledge of
the Author of the world, Who in the beginning created the world out of nothing,
and set everything in number, measure and weight, and then, in time and the
age of man, formulated a science which reveals fresh wonders the more we
study it.
 |
| Johann Kepler 1571-1630 |
Or listen to Kepler in Harmonia Mundi
(1619):
I thank thee, O Lord, our Creator, that thou hast permitted
me to look at the beauty in thy work of creation; I exult in the works of
thy hands. See, I have completed the work to which I felt called; I have
earned interest from the talent that thou hast given me. I have proclaimed
the glory of thy works to the people who will read these demonstrations,
to the extent that the limitations of my spirit would allow.
These, of course, are instances of the Platonic idea that
mathematical law and the harmony of nature are aspects of the divine
mind-soul. In this frame of reference, the Euclid myth discussed in Chapter
7 appears as an essential and congruous element.
Belief in a nonmaterial reality removes the paradox from the problem of
mathematical existence, whether in the mind of God or in some more abstract
and less personalized mode. If there is a realm of nonmaterial reality, then
there is no difficulty in accepting the reality of mathematical objects which
are simply one particular kind of nonmaterial object.
Who wields the compass? God? Archimedes? John Dee? Or does the compass wield itself? |
||
| Archimedes wields the compass. |
|
|
|
||
| Dr Dee wields the compass. From French,John Dee. |
||
|
The compass wields itself. The mystical Compass,From Robert Fludd, Ultriusque cosmi - historia,II (i). p28 (p407) From Yates "Giordano Bruno" |
|
God wields the compass. |
||
So far, we have discussed the interaction between the discipline of mathematics
and established religions. We might also ask to what extent does mathematics
itself function as a religion. Insofar as the "laws of mathematics" are
properties possessed by certain shared concepts, they resemble doctrines
of an established church. An intelligent observer seeing mathematicians at
work and listening to them talk, if he himself does not study or learn
mathematics, might conclude that they are devotees of exotic sects, pursuers
of esoteric keys to the universe.
Nonetheless, there is remarkable agreement among mathematicians.
While theologians notoriously differ in their assumptions about God, still
more in the inferences they draw from these assumptions, mathematics seems
to be a totally coherent unity with complete agreement on all important
questions; especially with the notion of proof
a procedure by which a proposition about the unseen reality can be
established with finality and accepted by all adherents. It can be observed
that if a mathematical question has a definite answer, then different
mathematicians, using different methods, working in different centuries,
will find the same answers.
Can we conclude that mathematics is a form of religion, and in fact the
true religion?
Further Readings. |
The Mathematical Experience Study Edition |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |