There is a mysterious boundary between the familiar predictability of ordinary objects and the spooky uncertainties of the quantum world. Now physicists are on the verge of discovering what happens there, says Mark Buchanan
The quantum world is famous for its weirdness : its particles
live in an eerie world of uncertainties and ghostly multiple existences.
We, on the other hand, are surrounded by robust and solid certainty. It might
be handy to be in two places at once, but we'll never manage it. Although
this separation of the microscopic and the everyday might seem perfectly
natural, in fact it's anything but. According to quantum theory, quantum
coexistence is infectious : it should percolate up from the atomic world
to ours, and afflict us all. So why doesn't it?
This question has baffled some of the greatest minds in physics:
Schrödinger,
Einstein,
Dirac and
Feynman
all failed to make sense of it. But now, some 70
years after quantum theory first upset the apple cart, salvation may finally
be at hand. In the past few years, some daring physicists have invented an
ingenious new twist to the theory that could finally unite the two worlds.
Erwin Schrödinger, one of the theory's founders, was the
first to point out that quantum weirdness should invade
the classical
world. He illustrated the point with a famous
thought experiment, which arranges a direct
link from the quantum world to ours. It works like this. In a box sits a
radioactive nucleus, a gun and a cat. Because it is radioactive, the nucleus
can decay and emit a neutron. Things are arranged so the neutron will trigger
the gun to shoot the cat.
If the nucleus remains whole, the cat lives, and if it decays,
the cat dies. But being a quantum particle, the nucleus doesn't have to choose
between its two possible states. Instead, it develops gradually into a strange
combination of both-called a
"superposition". Because of the link,
the split existence of the nucleus infects the cat as well. So if the nucleus
stays in its ghostly superposition of states, the cat stays in a ghastly
coexistence between life and death.
This conclusion follows unavoidably from the theory. But it
seems like pure nonsense. Cats are either alive or dead-there is no in-between.
Isn't this just proof that something is dreadfully wrong with the theory?
Schrödinger thought so, and so did Einstein , who quipped that "if quantum
physics is correct, then the world is
crazy" . But neither could work
out how to fix it. Meanwhile, it was becoming increasingly obvious in the
1930s that quantum theory worked very well for atoms and molecules. So physicists
devised an artificial solution. They just tacked an extra rule onto the theory
to forbid superpositions in big objects.
This extra rule -known as the "measurement postulate"-says
that the multiple existences of any object will collapse back to a single
existence whenever the object interacts with a " classical measuring device"
That could be all sorts of things -a photographic plate, the eye of a human
being, or any other big object. In essence, the measurement postulate says
that big things don't get into superpositions because superpositions collapse
whenever they encounter big things. It's a policeman,patrolling the border
between classical and quantum worlds, and keeping multiple existences down
where they belong.
This artifice is effective for most practical purposes, but
it still leaves a mighty split between the quantum and classical worlds.
The postulate clearly says that there are some things, such as electrons
and protons, that act according to quantum rules, and others , such as
photographic plates and experimenters, that follow classical (non-quantum)
rules. There are two separate domains with their own distinct laws of physics.
So much for a unified theory of the world.
In their desperation to get rid of the ugly split, physicists
have invented countless schemes designed to show that the extra measurement
postulate arises somehow out of the combined action of the more natural rules
of quantum theory. But it simply cannot. The ordinary quantum rules preserve
multiple existences, whereas the measurement postulate destroys them, so
trying to wring one from the other is hopeless. John Bell, the world's foremost
quantum expert until his death in 1990, likened the effort to a snake trying
to swallow itself by the tail. "It can be done up to a point," he said. "But
it becomes embarrassing for the spectators even before it becomes uncomfortable
for the snake."
Radical trio
So what is to be done? If quantum theory can't make sense of the single
existences of ordinary objects, it clearly needs some help. But the problem
is so staggeringly difficult that for many years only a few physicists even
tried to solve it. Then in 1986, three Italian physicists had a brilliant
idea. Aware of the early concerns of Einstein and Schrödinger, Gian-Carlo
Ghirardi of the University of Trieste, Alberto Rimini of the University of
Pavia, and Tullio Weber, also of Trieste, reckoned that the measurement postulate
disguised a deeper problem with the quantum rules themselves. Change these
, they thought, and perhaps you can drop the measurement rule.
In quantum theory, a "particle" does not sit in just one place,
but occupies many places all at once. Its true position is defined by a fuzzy
blob called a "wave function", which sets out the probability of finding
the particle in various locations. With time, the wave function of any particle
spreads out, bleeding into an expanding volume of space, as the particle's
multiple existences proliferate.
Ghirardi, Rimini and Weber proposed a subtle change in the
quantum rules that determine how wave functions evolve . Suppose, they said,
wave functions usually spread out according to normal quantum rules, but
very rarely-once every 100 million years or so -the wave- function of a single
particle collapses and becomes localised to a tiny region. This change scarcely
affects single particles, but has a huge effect on big things.
A cat or any other object of similar size contains some 1027
particles. And even though the wave function of any one is likely to
take 100 million years to collapse, there are so many particles that it is
overwhelmingly likely that the wave function of at least one particle will
collapse within just 10-12 seconds. What's more , because the
particles in an object interact with one another, their wave- functions are
entangled. The normal quantum rules then demand that the collapse in one
particle instantaneously triggers a collapse in all the others. The collapse
of one particle's wave function drags the whole lot into a definite state.
So in the scheme of Ghirardi, Rimini and Weber,
electrons and protons act as they should, and remain in superpositions for
long times, but weird living- dead cats are -within a mere trillionth of
a second-either spared or put out of their misery. All this follows naturally
from the theory, without any extra rules slapped on. There is no need to
divide the world into separate sets of laws.
This is an impressive achievement. And yet, the GRW theory has
some big problems of its own. After all, it doesn't begin to explain what
would make a wave function collapse, nor why it should happen only every
100 million years.
Also, according to Ian Percival, a physicist at Queen Mary and
Westfield College in London, the idea flies in the face of the way nature
usually works. He points out that in virtually all processes in the physical
world , changes over longer time intervals come about by the accumulation
of changes over shorter intervals. But in the GRW scheme, the interruptions
on long times that lead to collapse don't arise naturally from any processes
over shorter times. So it's difficult to imagine what might cause them.
Still unpalatable
This makes the GRW scheme almost as unpalatable as the ordinary quantum theory
with its bolted-on measurement rule. But in the past few years, some
new ideas have emerged that show how these
problems might be solved. Most notably, Percival, along with Nicholas Gisin
of the University of Geneva, has developed "quantum state diffusion theory",
which stands the GRW picture on its head.
Percival's and Gisin's idea was born of an analogy with an old
problem in physics-Brownian motion. If you peer through
a microscope at a dust particle floating in water, you'll see that it bounces
around erratically, rather like a ball in a pinball machine. This
"Brownian motion" is all down to molecules
. What happens is that in a liquid, the molecules move about violently, zinging
this way and that. A speck of dust endures a constant barrage of such molecules,
and the knocks it receives at their hands cause its erratic jitter.
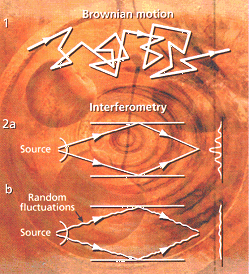A dust particle in the air does much the same
thing, but in between molecular collisions, gravity relentlessly drags it
down (see Diagram, opposite). Over very short periods of time, the irregular,
"noisy" part of this motion is most evident as the dust particle flits to
and fro. But over long times, the many irregular motions add up, and out
of the erratic jitter emerges the particle's downward drifting motion.
What does this have to do with quantum theory? Percival and
Gisin see the natural and continuous spreading motion of a quantum particle's
wave function as a kind of drift, albeit of a more abstract kind. In normal
quantum theory, this drift is all there is. But in the GRW scheme, the wave
function's continuous drift (spreading) is interrupted every 100 million
years or so by a sudden, random event that drives it to collapse again to
a small volume. These random hits are rather like the molecular collisions
of Brownian motion, but the GRW picture doesn't quite fit the analogy. In
the GRW model, random collapse events tend to be separated by long periods
of time, during which a great deal of drift occurs. But the erratic events
in Brownian motion happen very frequently, and drift emerges as these rapid
events accumulate.
To develop a more natural theory, Gisin and Percival suggest
that the random fluctuations happen over very short periods, so that the
state of a quantum system follows a sort of Brownian motion. Over very short
periods, the irregular part of the motion is most important, and the wave
function fluctuates haphazardly. But over longer periods, the fluctuations
add up to give a steady development, and the wave function spreads as expected
from normal quantum theory.
But Percival and Gisin also include another element in their
equations which spell the end for multiple existences. This property of the
equations, known as
"nonlinearity" arms the quantum
world against itself. In effect, the nonlinearities force the different partial
existences of an object to struggle against one another for supremacy, until
all but one have been eliminated, and the wave- function has collapsed.
Just as in the GRW theory, collapse happens very slowly for
single particles, but very quickly for big ones. It works in much the same
way. On average , the struggle between the partial existences of any single
particle takes a very long time. But because of the random fluctuations it
can sometimes -rarely-happen quickly. Given the huge number of particles
in an ordinary object, it is overwhelmingly likely that at least one of them
will have collapsed back to a single existence in a tiny fraction of a second.
This collapse drags the entire collection of particles with it, so the whole
object reverts to a single existence.
Field in flux
This theory certainly seems to do the trick. But what could be causing the
fluctuations? One intriguing hypothesis is that they reflect irreducible
fluctuations in the very fabric of space-time itself. Tentative attempts
by physicists to build a quantum version of Einstein's general relativity-
which views gravity as curvature in the geometry of space-time -suggest that
the Universe's gravitational field should fluctuate rapidly over distances
and times of about 10-35 metres and 10-44 seconds.
So it may be that these very fluctuations are popping up in Percival and
Gisin's theory.
If so, it would seem that tangible effects of quantum gravity
are all around us, prohibiting multiple existences in big objects and keeping
Schrödinger's cat in one piece.
Even more remarkably, Percival and Gisin believe that it may soon be possible
to detect these fluctuations in the laboratory. Not directly, to be sure.
But they should have measurable effects on delicate interference experiments.
Imagine a beam of particles split into partial existences which are sent
along different paths (see Diagram) . According to quantum theory, each particle
is like a clock that oscillates with a characteristic frequency. So the number
of ,cycles it goes through by the time it gets to the screen depends on how
long it takes to get there. When they arrive , the partial existences interfere
with one another, forming a pattern that depends on small differences in
the number of cycles each clock has gone through.
But space-time fluctuations along the paths could disturb these relationships
- because the fluctuations should make the clocks speed up or slow down
erratically as they travel. So the clock settings of the ,two partial existences
at the screen will vary randomly and the expected pattern will be destroyed.
In 1992, Mark Kasevich and Steven Chu of Stanford University
directed two beams of sodium atoms along different paths some 15 centimetres
long, and found the pattern expected from normal fluctuations-if noticeable
effects. These experiments would be sensitive enough to detect the fluctuations
if they take place in around 10-44 seconds.
But the fluctuations may well be more rapid yet. One way to
improve the sensitivity of the experiments would be to allow the beams of
atoms to travel over longer distances before they interfere with each other.
This is trickier, because external noise would be harder to eliminate. But
it would give the effects of the fluctuations more time to accumulate, and
should provide a more sensitive probe within the next few years.
If the fluctuations are detected, these new theories will
undoubtedly displace ordinary quantum theory. Theoretical
physicist Roger
Penrose of Oxford University believes that this would be an important
step forward. But he suspects that a more radical break with the ideas of
ordinary quantum theory is needed.
"I think there has to be a very major revolution in the way we look at quantum
mechanics," he says.
He points out, for example, that any superposition of states
necessarily leads to a superposition of universes with different space-time
geometries . And that spells trouble. Consider the cat when it is suspended
between life and death. In one existence the cat lies dead on the floor.
In the other, it prowls its cage. So the Universe exists in a superposition
of states with different mass distributions.
Using the details of the general theory of relativity, Penrose
argues that this situation would undermine the very notion of energy-rather
than being a well-defined quantity, energy would become vague and uncertain.
In such a world, the crucial principle of the conservation of energy would
be in trouble.
Penrose suggests that a Universe in this dilemma would be unstable,
and would fall naturally into one state or the other, eliminating the
superposition. And he suggests that the decay would be more rapid for
superpositions involving more widely differing distributions of mass - for
bigger particles, for instance, or for objects involving many particles.
These ideas would achieve the same sewing-up of the classical and quantum
worlds as Gisin and Percival's theory, but would also make a real connection
to the theory of gravity."I am not proposing a theory," says Penrose. "I
am only saying that this is the kind of level at which something new has
to come in."
These are exciting times for quantum physics. After 70 years,
Schrödinger's and Einstein's worries have finally borne fruit, and the
ugly divide between the quantum and classical worlds looks likely to be bridged.
Whatever the details of the ultimate theory, it may turn out to be both more
and less bizarre than Schrödinger and Einstein suspected.
[http://www.nsplus.com/]
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
New Scientist 26 Apr 1997 File Info: Created Updated 22/8/2006 Page Address: http://members.fortunecity.com/templarser/qfront.html