|
|
|
|
|
|
|
|
|
Confronting Science's Logical Limits
by John L.Casti
The mathematical models now used in many scientific fields may be
fundamentally unable to answer certain questions about the real world. Yet
there may be ways around these problems.
To anyone infected with the idea that the human mind is unlimited
in its capacity to answer questions, a tour of 20th-century mathematics must
be rather disturbing. In 1931 Kurt Gödel
set forth his
incompleteness
theorem, which established that no system of deductive inference can
answer all questions about numbers. A few years later
Alan M. Turing
proved an equivalent assertion about computer programs, which states that
there is no systematic way to determine whether a given program will ever
halt when processing a set of data. More recently,
Gregory J. Chaitin of IBM
has found arithmetic propositions whose truth can never be established by
following any deductive rules.
 |
TRAVELLING SALESMAN would need the world's fastest computer
running for billions of years to calculate the shortest route between 100
destinations. Scientists are now seeking ways to make such daunting problems
more tractable. |
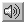 |
| RUSH |
These findings proscribe our ability to know in the world of mathematics
and logic. Are there similar limits to our ability to answer questions about
natural and human affairs? The first and perhaps most vexing task in confronting
this issue is to settle what we mean by "scientific knowledge." To cut through
this philosophical Gordian knot, let me adopt
the perhaps moderately controversial position that a scientific way of answering
a question takes the form of a set of rules, or program. We simply feed the
question into the rules as input, turn the crank of logical deduction and
wait for the answer to appear.
Thinking of scientific knowledge as being generated by what amounts
to a computer program raises the issue of computational intractability. The
difficulty of solving the celebrated travelling
salesman problem, which involves finding the shortest route connecting
a large number of cities, is widely believed to increase exponentially as
the number of destinations rises. For example pinpointing the best itinerary
for a, salesman visiting 100 cities would require examining 100 x 99 x 98
x 97 x...x 1 possibilities-a task that would take even the fastest computer
billions of years to complete.
But such a computation is possible-at least in principle. Our focus
is on questions for which there exists no program at all that can produce
an answer. What would be needed for the world of physical phenomena to display
the kind of logical unanswerability seen mathematics ? I contend that nature
would have to be either inconsistent or incomplete, in the following senses.
Consistency means that there are no true paradoxes in nature. In general,
when we encounter what appears to be such a paradox-such as jets of gas that
seemed to be ejected from quasars at faster than light speeds-subsequent
investigation has provided a resolution. (The " super- luminal" jets turned
out to be an optical illusion stemming from relativistic effects.)
 |
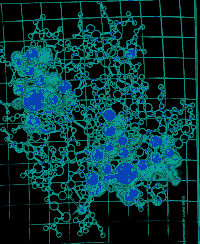 |
PROTEIN FOLDING PROBLEM considers how amino acids (left)
folds up instantaneously into extraordinarily complex, three-dimensional
protein (right) Biologists are no trying to unravel the biochemical "rules"
that proteins follow in accomplishing this feat. |
Completeness of nature implies that a physical state cannot arise for
no reason whatsoever; in short, there is a cause for every effect. Some analysts
might object that quantum theory contradicts the claim that nature is consistent
and complete. Actually, the equation governing the wave function of a quantum
phenomenon provides a causal explanation for every observation (completeness)
and is well defined at each instant in time (consistency ) . The notorious
"paradoxes" of quantum mechanics arise because we insist on thinking of the
quantum object as a classical one.
A Triad of Riddles
It is my belief that nature is both consistent and complete. On the other
hand, science's dependence on mathematics and deduction hampers our ability
to answer certain questions about the natural world. To bring this issue
into sharper focus, let us look at three well-known problems from the areas
of physics, biology and economics.
Stability of the solar system. The most famous question of
classical mechanics is the
N-body problem. Broadly speaking, this
problem looks at the behaviour of a number, N, of point-size masses moving
in accordance with
Newton's law of gravitational attraction.
One version of the problem addresses whether two or more of these bodies
will collide or whether we will acquire an arbitrarily high velocity in a
finite time.In his 1988 doctoral dissertation,Zhihong ( Jeff ) Xia of
Northwestern University showed how a single body moving back and forth between
two binary systems (for a total of five masses) could approach an arbitrarily
high velocity and be expelled from the system. This result, which was based
on a special geometric configuration of the bodies, says nothing about the
specific case of our solar system. But it does suggest that perhaps
the solar
system might not be stable .More important,
the finding offers new tools with which to investigate the matter.
Protein folding. The proteins making
up every living organism formed as sequences of a large number of amino acids,
strung out like beads on a necklace. Once the beads are put in the right
sequence, the protein folds up rapidly to a highly specific three-dimensional
structure that determines its function in the organism. It has been estimated
that a supercomputer applying plausible rules for
protein folding would need 10127
years to find the final folded form for even a very short sequence
consisting of just 100 amino acids. In fact in 1993 Aviezri S. Fraenkel of
the University of Pennsylvania showed that the mathematical formulation of
the protein-folding problem is computationally "hard" in the same way that
the travelling-salesman problem is hard. How does nature do it?
Market efficiency. One of the pillars
on which the classical academic theory of finance rests is the idea that
markets are "efficient." That is,the market
immediately processes all information affecting the price of a stock or commodity
and incorporates it into the current price of the security. Consequently
prices should move in an unpredictable,essentially random fashion discounting
the effect of inflation. This, in turn, means that trading schemes based
on any publicly available information, such as price histories, should be
useless; there can be no scheme that performs better than the market as a
whole over a significant interval. But actual markets do not seem to pay
much attention to academic theory. The finance literature is filled with
such market "anomalies" as the low price-earnings ratio effect, which states
that the stocks of firms whose prices are low relative to their earnings
consistently outperform the market overall.
The Unreality of Mathematics
Our examination of the three questions posed above has yielded what appear
to be three answers: the solar system may not be stable, protein folding
is computationally hard, and financial markets are probably not completely
efficient. But what each of these putative "answers" has in common is that
it involves a mathematical representation of the real-world question, not
the question itself. For instance, Xia's solution of the N-body problem does
not explain how real planetary bodies move in accordance with real world
gravitational forces. Similarly, Fraenkel's conclusion that protein folding
is computationally hard fails to address the issue of how real proteins manage
to do their job in seconds rather than eons. And,of course canny Wall Street
operators have thumbed their noses at the efficient-market hypothesis for
decades. So to draw any conclusions about inability of science to deal with
these questions,we must either justify the mathematical as a faithful
representation of the physical situation or abandon the mathematics altogether.We
consider both possibilities in what follows.
What these examples show is that if we want to look for scientifically
unanswerable questions in the real world,we must carefully distinguish between
the world of natural and human phenomena and mathematical and computational
models of those worlds.The objects of the real world consist of directly
observable quantities,such as time and position,or quantities,such as energy,that
are derived from them.Thus,we consider parameters such as the measured position
of planets or observed configuration of a protein. Such observables generally
constitute a discrete set of measurements taking their values in some finite
set of numbers. Moreover such measurements are generally not exact.
In the world of mathematics, on the other hand, we have symbolic
representations of such real-world observables, where the symbols are often
assumed to belong to a continuum in both space and time.The mathematical
symbols representing attributes such as position and speed usually have numerical
values that are integers, real numbers or complex numbers, all systems containing
an infinite number of elements. In mathematics the concept of choice for
characterising uncertainty is randomness.
Finally, there is the world of computation which occupies the curious
position of having one foot in the real world of physical devices and one
foot in the world of abstract mathematical objects. If we think of computation
as the execution of a set of rules,or algorithm, the process is a purely
mathematical one belonging to the world of symbolic objects.But if we regard
a computation as the process of turning switches on or off in the memory
of an actual computing machine,then it is a process firmly rooted in the
world of physical observables.
One way to demonstrate whether a given question is logically impossible
to answer by scientific means is to restrict all discussion and arguments
solely to the world of natural phenomena. If we follow this path, we are
forbidden to translate such questions as "Is the
solar system stable?" into a mathematical statement and thereby to generate
an answer with the logical proof mechanism of mathematics. We then face the
problem of finding a substitute in the physical world for the concept of
mathematical proof.
A good candidate is the notion of causality.A question can be considered
scientifically answerable,in principle,if is it is possible to produce a
chain of causal arguments whose final link is the answer to the question.A
causal argument need not be expressed in mathematical terms. For example,the
standard deductive argument
"All men are
mortal;Socrates is a man;therefore,Socrates
is mortal" is a causal chain.There is no mathematics involved, just plain
English. [But it can be represented by set theory or
fuzzy logic,but it is the notion of why a thing
belongs in one set rather than another,which is the kind of thing
Roger Penrose suggests is only available
to human reasoning as opposed to AI digital computers-LB] On the other hand,
constructing a convincing causal argument without recourse to mathematics
may be a daunting task. In the case of the stability of the solar system,
for example, one must find compelling nonmathematical definitions of the
planets and gravity.
 Given these difficulties,it seems wise to consider approaches
that mix the worlds of nature and mathematics. If we want to invoke the proof
machinery of mathematics to settle a particular real world question, it is
first necessary to "encode" the question as a statement in some mathematical
formalism, such as a differential equation, a graph or an N-person game.
We settle the mathematical version of the question using the tools and techniques
of this particular corner of the mathematical world, eventually "decoding"
the answer (if there is one! ) back into real-world terms. One challenge
here is establishing that the mathematical version of the problem is a faithful
representation of the question as it arises in the real world. How do we
know that mathematical models of a natural system and the system itself bear
any relation to each other? [This is the question which bothers me,L-systems
look like plants and Fractals like mountains,but is the similarity superficial
or fundamental? In some sense they are the same because the model was constructed
from the real world object and is "observed" to be doing the same thing like
"branching" etc -LB This is an old philosophical conundrum, entailing the
development of a theory of models for its resolution. Moreover, mathematical
arguments may bet subject to the constraints revealed by Gödel, Turing
and Chaitin;we do not know yet whether the real world is similarly
constrained. Given these difficulties,it seems wise to consider approaches
that mix the worlds of nature and mathematics. If we want to invoke the proof
machinery of mathematics to settle a particular real world question, it is
first necessary to "encode" the question as a statement in some mathematical
formalism, such as a differential equation, a graph or an N-person game.
We settle the mathematical version of the question using the tools and techniques
of this particular corner of the mathematical world, eventually "decoding"
the answer (if there is one! ) back into real-world terms. One challenge
here is establishing that the mathematical version of the problem is a faithful
representation of the question as it arises in the real world. How do we
know that mathematical models of a natural system and the system itself bear
any relation to each other? [This is the question which bothers me,L-systems
look like plants and Fractals like mountains,but is the similarity superficial
or fundamental? In some sense they are the same because the model was constructed
from the real world object and is "observed" to be doing the same thing like
"branching" etc -LB This is an old philosophical conundrum, entailing the
development of a theory of models for its resolution. Moreover, mathematical
arguments may bet subject to the constraints revealed by Gödel, Turing
and Chaitin;we do not know yet whether the real world is similarly
constrained.
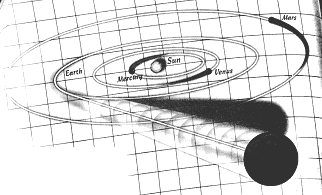 |
N-BODY SYSTEM consisting of a point mass oscillating
between two binary systems (above) is unstable,according to a theorem
by Zhihong Xia of Northwestern University. Such work may
reveal whether the solar system will someday expel one of
its planets into deep space. |
The Noncomputational Mind
There may be ways to sidestep these issues. The problems identified by
Gödel and others apply to number systems with infinite elements, such
as the set of all integers. But many real-world problems such as the
travelling-salesman problem, involve a
finite number of variables,each of which can take only a finite number of
possible values.
Similarly, nondeductive modes of reasoning-induction, for instance,
in which we jump to a general conclusion on the basis of a finite number
of specific observations - can take us beyond the realm of logical
undecidability. So if we restrict our mathematical formalisms to systems
using finite sets of numbers or nondeductive logic, or both, every mathematical
question should be answerable; hence, we can expect the decoded real-world
counterpart of such questions to be answerable as well.
 Studies of human mind may reveal
other ways to bypass logical limits. Some artificial-intelligence proponents
have proposed that our brains are computers, albeit extremely sophisticated
ones, that perform calculations in the same logical, step,by-step fashion
that conventional computers (and even parallel processors and neural networks)
do. But various theorists, notably the mathematical physicist
Roger Penrose of the University of Oxford,
have argued that human cognitive activity is not based on any known deductive
rules and is thus not subject to Godelian limits. Studies of human mind may reveal
other ways to bypass logical limits. Some artificial-intelligence proponents
have proposed that our brains are computers, albeit extremely sophisticated
ones, that perform calculations in the same logical, step,by-step fashion
that conventional computers (and even parallel processors and neural networks)
do. But various theorists, notably the mathematical physicist
Roger Penrose of the University of Oxford,
have argued that human cognitive activity is not based on any known deductive
rules and is thus not subject to Godelian limits.
Recently this viewpoint has been bolstered by studies carried out under
the aegis of the Institute for Future Studies in Stockholm by me, the
psychologist Margaret A. Boden of the University of Sussex, the mathematician
Donald G. Saari of Northwestern University, the economist Ake E. Andersson
(the institute's director) and others. Our work strongly suggests that in
the arts as well as in the natural sciences and mathematics, the human creative
capacity is not subject to the rigid constraints of a computer's calculations.
Penrose and other theorists have conjectured that human creativity stems
from some still unknown mechanisms or rules, perhaps related to quantum
mechanics. By uncovering these mechanisms and incorporating them into the
scientific method, scientists may be able to solve some seemingly intractable
problems.
Of course, science's ability to plumb nature's secrets is limited by
many practical considerations-such as measurement error,length of computation,
physical and economic resources, political and cultural values. But none
of these considerations bears on whether there is a logical barrier to our
answering a certain question about the natural world. My contention is that
there is not. So a tour of 20th-century mathematics need not be so disturbing
after all !
The Author JOHN L. CASTI is a professor
at the Technical University of Vienna and at the Santa Fe Institute
(casti@santafe.edu). He is grateful to Joseph F. Traub, Piet Hut, James B.
Hartle and Ake E. Andersson for stimulating discussions on these matters
and to the lnstitute for Future Studies in Stockholm for partial support
of this research.
| Loops
and folds of our DNA to shed light on disease
18:25 11 December 2014 by Clare Wilson
For similar stories, visit the Genetics Topic Guide
Lots of things look clearer in 3D, and that goes for the genome
too.
The human genome was sequenced about 10 years ago, but that still
left us with much to learn about its structure and function. Some of the
gaps have since been filled, but how our full complement of DNA – 1.8
metres long when stretched out – fits into the nuclei of our cells remained
elusive.
Now the way DNA folds and loops in on itself inside the nucleus has
been mapped in unprecedented detail in nine cell types, including lung, skin
and immune cells. The work is the first draft of the 3D genome, also known
as the loopome, or nucleome.
It's important to chart these undulations because they help control
which genes are turned on and off. "The loopome will lead to amazing insights
into how cells work, normally and in disease," says Suhas Rao of Baylor College
of Medicine in Houston, Texas, who took part in the work.
Physically close
The team showed that the loops usually fall in a way that means they bring
protein-coding genes physically close to control switches – DNA sequences
that turn genes on or off.
About half of the 10,000 loops the researchers identified were common
to all nine cell types, with the rest specific to different cells.
The work has also shed light on how loops are formed. A protein called
CTCF can bind to both DNA and itself. Two units of CTCF that face in opposite
directions must unite to bring together two regions of a DNA strand, causing
a loop to form in between them.
'The work took five years, but it's just the start. In July, the US
National Institutes of Health announced funds for research to understand
and catalogue the loopome in different cell types, and how they change over
time, in health and disease.
Melissa Fullwood of the Cancer Science Institute of Singapore, who
is studying how the loopome changes in cancer, says: "What's amazing about
this is that they have got such a high level of resolution. These are the
first steps. Ideally in the future, we will repeat this with many different
cell types."
Fullwood predicts that in future, people's cancer cells will not just
be tested for their gene mutations, but also for how their loopomes have
changed to see which genes have been turned on or off.
Journal reference: Cell, DOI: 10.1016/j.cell.2014.11.021
|
Further Reading
SEARCHING FOR CERTAINTY. John L.Casti. William Morrow,1991.
RANDOMNESS AND UNDECIDABILITY IN PHYSICS. K.Svovil World Scientific, Singapore,
1994.
BOUNDARIES AND BARRIERS. Edited by John L. Casti and A.Karlqvist. Addison
-Wesley, 1996.
GAME THEORY-THE TRAVELLER'S DILEMMA.Kaushik Basu |
|
|
|
|
|
|
|
|
|
|