 |
Prime Pursuits
|
Ivars Peterson
PRIME PROPERTIES
The study of prime numbers has long been a central part of number theory,
a field traditionally pursued for its own sake and for the beauty of its
results. Once thought to be the purest of pure mathematics, this ancient
pastime now figures prominently in modern computer science. The security
of modern cryptosystems depends very strongly on the twin questions of how
easy it is to identify primes and how hard it is to factor a large, random
number. Neither question has a clear answer yet.
Divisible evenly only by themselves and the number 1, the primes stand at
the center of number theory. Like chemical elements in chemistry or fundamental
particles in physics, they are building blocks in the mathematics of whole
numbers. All other whole numbers, known as composites, can be written as
the product of smaller prime numbers. In fact, according to the fundamental
theorem of arithmetic, each composite number has a unique set of prime
factors. Hence, the composite number 20 can be broken down into the prime
factors 2, 2, and 5. No other composite number has the same set of factors.
The number 1 is considered to be neither prime nor composite.
Whereas chemists have only a hundred or so elements to play with, mathematicians
interested in number theory must deal with an endless supply of primes.
More than 2,000 years ago, Euclid
proved that there is an infinite number of primes, and mathematicians
ever since have been caught up in the never-ending pursuit of primes. Euclid's
argument is instructive. His proof relies on establishing a result that
contradicts his initial assumption. The proof
begins with the idea of a finite number of primes, with some largest
prime, p. If all the primes are multiplied together and 1 is added
to this gigantic product, a new number, N, emerges that is larger
than p. If the initial assumption is correct, then N can't
be prime because otherwise it would be the largest prime. It must be a composite
and divisible by at least one smaller prime number. However, because of the
way N was put together, all known primes, when divided into N,
would leave a remainder of 1. Therefore, N must be a prime that is
larger than p. This contradicts the starting assumption and forces
the conclusion that there can be no largest prime. There are, instead,
infinitely many primes.
With such a vast array of numbers to work with, finding primes shouldn't
be difficult. However, because prime numbers behave perversely and are
scattered among
the whole numbers in seemingly unpredictable ways, special nets are needed
to catch them. Euclid's proof suggests one potential method for constructing
prime numbers: multiply together all primes up to a certain value, then add
1.Is the result always a prime number? A simple experiment is revealing:
2 + 1 = 3;
2 x 3 + 1 = 7;
2 x 3 x 5 + 1 = 31;
2 x 3 x 5 x 7 + 1 = 211;
2 x 3 x 5 x 7 x 11 + 1 = 2,311.
It looks promising. But 2 x 3 x 5 x 7 x 11 x 13 +1= 30,031 =59 x 509
In fact,the next four instances prove to be composites. Further explorations
show that Euclid's construction often but not always produces a prime.
In prime-number theory, simple, reasonable questions are remarkably easy
to ask, yet many of these questions are surprisingly difficult or even impossible
to answer. Is there a general formula that reliably generates prime numbers?
Given a prime number, how far is it to the next one? Are there infinitely
many twin primes, or consecutive pairs, such as 3 and 5, 41 and 43, and so
on? No one knows yet. And there are dozens of similar conjectures waiting
for proofs.
Fortunately, students of primes do have a systematic, though computer-consuming,
way to trap primes and separate them from composites. Of course, they use
a sieve for such a job. This particular sieve was discovered in the third
century B.C. by Eratosthenes of Cyrene and goes by his name. The sieve of
Eratosthenes generates a list of prime numbers by the process of elimination.
To find all prime numbers less than, say, 100, the pursuer writes down all
the integers from 2 to 100.First,2 is circled, and all multiples of 2 (4,
6, 8,... are struck from the list .That eliminates all composite numbers
that have 2 as a factor. This step incidentally, also confirms that 2 is
the only even prime number a rather odd result, some would say.
The next unmarked number is 3. That number is circled, and all multiples
of three are crossed out. The number 4 is already crossed out, and its multiples
have also been eliminated. Five is the next unmarked integer,and the procedure
continues in this way until only prime numbers are left on the list. In this
example, the job finishes with 7 because 8,9 and 10 are already gone, and
11 is greater than the square root of 100,the largest number in the table.
All multiples of 11 less than 100 would already be crossed out. The sieve
ends up trapping 25 numbers - all the primes less than 100 (see Figure
2.1).
 |
| Figure 2.1 The sieve of Eratosthenes catches 25 primes among whole numbers less than 100. |
Although some shortcuts simplify the sieving, it remains a tedious,
time-consuming procedure, especially when the targets are dozens or hundreds
of digits long. Sieving is a serious business for number theorists, and because
they have no reliable formulas that automatically generate only prime numbers
of any desired size, they use the sieve of Eratosthenes to fill in the gap.
The claims of some mathematicians, both amateur and professional, to have
found a magic formula for primes have invariably turned out to be false.
In many cases, the formulas are merely cleverly disguised versions of the
ancient sieve of Eratosthenes.
Because so many important ideas in number theory seem resistant to definitive
analysis, experiment plays an important role in this field of mathematics
research. Although their work differs from the experimental research associated
with, say, test tubes and noxious chemicals, number theorists, like chemists
and other researchers, often collect piles of data before they can begin
to extract the principles that neatly account for their observations. Strict
reliance on deduction-the hops, steps, and jumps from one theorem or logical
truth to another that we usually associate with mathematics - isn't sufficient
in number theory.
| WAV 257K |
Few people outside of mathematics are aware of the field's empirical aspect.
Much of the mathematics encountered by high-school and college students seems
carved in stone, passed on unchanged from one generation to another. Yet
even the fundamental principles of arithmetic and plane geometry were once
the subjects of debate and speculation. It took centuries of constant
questioning. brilliant guesses, and steady refinements to build the edifice
now known as mathematics, and the structure continues to evolve. The
study of prime numbers is one of the few areas still left in mathematics
in which the concepts, questions and experiments are still simple enough
to intrigue both amateur and professional mathematicians. In fields such
as algebraic topology and differential geometry, usually only the professionals
and advanced graduate students experience the thrill of the quest.
The search for patterns and trends plays an important role in the study of
the distribution of prime numbers. Clearly, although Euclid proved that the
list of primes goes on forever, the stretches between primes, on the average,
get longer and longer (see Figure 2.2). The elimination of multiples of every
new prime encountered by the sieve of Eratosthenes nicely demonstrates the
increasing scarcity of primes among the larger integers.
At the same time, prime numbers appear to be scattered haphazardly throughout
the whole numbers. In 1896, French mathematician Jacques Radamard and Belgian
Charles de la vallee-Poussin used this idea to find an expression that precisely
describes the statistical distribution of primes. The theorem that they
independently proved is now known as the prime number
theorem. It proposes that the average distance between two consecutive
primes near the number n is close to the natural logarithm of
n. When n is close to 100, for instance. the natural logarithm
of n is approximately 4.6. In that range, every fifth number or so
should he a prime.
 |
| Figure 2.2 A computer-generated grid showing primes (white dots) as a spiral of integers from 1 to about 65,000. |
But the prime number theorem doesn't eliminate the element of surprise. It
doesn't specify exactly where a particular prime falls. That's left to the
innumerable tests and experiments that make up the gathering-of-data phase
of mathematics research. This data-collection operation now increasingly
involves computers, which have extended the list of known primes well beyond
the range of hand calculation.
Sometimes, tantalizing pattern fragments show up. The sequence 31, 331,
3331, 33331, 333331, 3333331, 33333331 looks promising: all the numbers
in that sequence are primes. Alas, it fails in the next step. The number
333333331 is a composite with factors 17 and 19607843. Such accidental patterns
lead nowhere.
Some simple equations can generate a surprising number of primes. The formula
x2 + x + 41, for example, produces an unbroken sequence
of 40 primes, starting with x=0 (see Figure 2.3). For values of
x up to 10,000, the formula produces primes almost half the time.
However, beyond 10,000, the proportion of primes inevitably decreases. Another
simple "prime-rich" formula", x2 + x + 17, also
discovered by the eighteenth-century Swiss mathematician
Leonhard Euler, generates primes for all values of
x from 0 through 15. However, mathematicians have proved that no
polynomial formula has only prime values, so a search for general formulas
similar to the ones illustrated is fruitless.
Primes often appear as pairs of consecutive odd integers: 3 and 5; 11 and
13; 41 and 43; 179 and 181; 209,267 and 209,269; and so on. These twins are
spread throughout the list of known prime numbers. Statistical evidence suggests
that there are infinitely many twin primes, and mathematicians have estimated
that in the range close to the number n, the average distance between
one pair of twin primes and the next is close to the square of the natural
logarithm of n. But no one has yet proved that there is an infinite
number of twin primes; it remains one of the major unsolved problems in number
theory. Over the last century, numerous mathematicians have attacked the
problem in a variety of ways, but all have failed. The optimists believe
that it may take another century of determined assaults before anyone succeeds.
At the same time, it's relatively easy to prove that consecutive primes can
be as far apart as anyone would want. The sequence of numbers n! +
2, n! +3, n! ..... . n! + n shows this conjecture
must be true. The expression n! (read as n factorial) is less a statement
of mathematical excitement than a shorthand way of writing the product of
all whole numbers from 1 to n. The number n!, where n = 5,
for example, has a value of 1 x 2 x 3 x 4 x 5, or 120. In the general case,
n! + 2 is evenly divisible by 2, n! + 3 is evenly divisible
by 3, and so on. Finally, n! + n is evenly divisible by n.
Therefore, all the numbers in the sequence are composite. The sequence can
be made arbitrarily long by picking a sufficiently large number n.
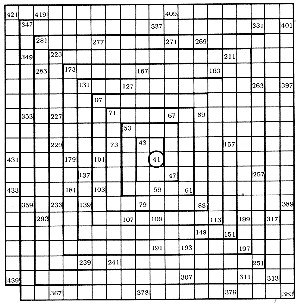 |
| Figure 2.3 The primes between 41 and 439 plotted on a square spiral beginning with 41 in the center.Values along the diagonal satisfy the formula x2 + x + 41 |
All their suggestive properties indicate that primes are not randomly scattered
among the integers, yet prime numbers, in their maddening perversity, defy
all attempts aimed at putting them precisely in their places. To try to prove
many conjectures about prime numbers, mathematicians therefore often must
devise sneaky strategems to get at their prey indirectly. They fence in the
unruly conjecture, first staking out a wide swath of territory before gradually
closing in on it. The pursuers then draw the net tighter, taking in corners
and cutting down boundaries while scrupulously checking for loop- holes.
Finally, if all goes well, the conjecture is trapped.
One such attempt is the continuing work on the Goldbach conjecture, which
views prime numbers as the building blocks of other numbers. The Prussian
mathematician Christian Goldbach suggested the idea
in a letter to Euler in 1742. His claim, expressed in modern terms, is that
every even number greater than 4 is the sum of two odd primes (that is, primes
other than 2). The number 32, for instance, is the sum of 13 and 19. This
proposition is now known as the "strong"
Goldbach conjecture. The "weak" Goldbach
conjecture holds that every odd number greater than 7 can be expressed as
the sum of three odd primes. In both cases, the same prime number may be
used more than once in a single sum.
Neither conjecture has yet been proved, but over the years, there have been
several near misses. In 1937, the Russian mathematician Ivan M. Vinogradov,
a leading number theorist, showed that all "sufficiently large" odd numbers
can be expressed as the sum of three primes. Although Vinogradov couldn't
state explicitly what "large enough" meant, in 1956, his student K. V. Borodzin
found that 3315 works as an upper bound. That number
has more than 6 million digits. If all odd numbers smaller than
3315 are the sum of three primes, then the weak Goldbach
conjecture is proved.
Computer searches have verified both the strong and weak conjectures up to
at least a million. Mathematicians have also proved that if the weak conjecture
is false, then there are only a finite number of exceptions. Thus the trap
is closing in on the weak conjecture, and many mathematicians now regard
it as "essentially" proved. The strong version is somewhat more elusive,
but in 1966, Chinese mathematician Chen Jing-run showed that all large enough
numbers can be expressed as the sum of a prime number and a number that is
either prime or the product of two primes. The net tightens.
Despite such successes, some number theorists believe that certain central
questions about prime numbers may have no solutions. In 1931, a startled
mathematical world had to confront and learn to live with such a possibility,
not just in number theory but everywhere in mathematics. Austrian mathematician
and logician Kurt Gödel
proved that any collection of axioms, such as those underlying euclidean
geometry or the theory of infinite sets, leads to a mathematical system
containing statements that can be neither proved nor disproved on the basis
of those axioms. A theorem, then, can be undecidable: adding more axioms
wouldn't help because some theorems would still slip through. Furthermore,
Gödel's work implies that in some cases, mathematicians wouldn't even
be able to decide whether a theorem can or cannot be proved. Uncertainty
strikes in mathematics!
Various guesses about prime numbers, perhaps even the strong Goldbach
conjecture, may truly turn out to be undecidable. Few mathematical fields
other than number theory have so high a proportion of widely believed but
unproved propositions. This doesn't mean that the conjectures are all likely
to be false, but it implies that for some conjectures, an airtight case might
not exist, despite the steady accumulation of persuasive evidence in its
favour. Mathematical proofs require more than
just overwhelming evidence.
Even so, the quest isn't hopeless. Near misses and proofs that confirm special
cases or parts of conjectures hint that eventually techniques may be developed
to handle the problems-although it could take centuries. That is far different
from saying that a conjecture can never be proved, for a single breakthrough
could put such suppositions as the number of twin primes suddenly within
reach. Meanwhile, with the use of computers, specific knowledge about prime
numbers is growing steadily, although considering the centuries of effort
put in by numerous mathematicians, the theory of prime numbers still seems
meagre.
