 |
Prime Pursuits
|
Ivars Peterson
BREAKING UP IS HARD TO DO
A decade or so ago, an interest in factoring was the mark of an eccentric.
Only a handful of number theorists cared to wrestle with lengthy strings
of digits. This small, obscure group of mathematicians worked quietly, prying
open large composite numbers to unlock their prime secrets. They revelled
in the pure delight of calculation and in the pleasure of devising elegant
algorithms to do their work. Like many ardent hunters, they even kept a list
of "wanted" and "most wanted" targets (see Figure 2.5).
Those mathematicians are still around, but they have been joined by a crowd
of computer scientists and applied mathematicians eager to test their skills.
Armed with advanced algorithms, sophisticated computers, and specialized
calculating machines, the newcomers are rapidly changing the formerly sedate
and sheltered world of factoring. In just a few years, successful factorizations
of "hard" numbers have jumped from numbers with 50 decimal digits to those
with more than 80. Now, the list of "most wanted" factorizations must be
updated regularly.
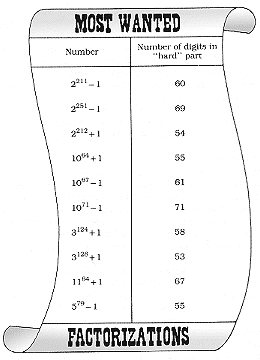 |
| FIGURE 2.5 The 1983 list of "most wanted" factorizations. Some of these numbers have a small, easy-to-find divisor, but that still leaves a "hard" part. A specially programmed supercomputer was able to crack all these numbers in the space of a year. |
Factoring is of considerable interest because the security of several important
cryptographic systems depends on the difficulty of factoring numbers with
100 or more digits. Without doubt, compared with testing for primality, factoring
is hard. It takes a day or so of supercomputer time to break an 80-digit
number that happens to have no small factors. It would take only a few seconds,
if that, to tell whether the number is a prime. Much current research is
aimed at providing as sharp an estimate as possible of how hard factoring
really is.
The most obvious, systematic way to find the factors of a number N
is by trial division. If 2 doesn't divide evenly into N, then 3 may,
or 4, or 5, and so on. The first number that divides evenly into N
is a prime factor. Dividing N by that factor and then starting the
process all over again eventually leads to the full "prime decomposition"
of N. To speed up the process, we can divide only by primes rather
than by every integer up to N - 1; furthermore, we need not use trial
divisors beyond the square root of N. This enhanced trial-division
algorithm, as fine-tuned by computer scientists, works well for numbers that
have 10 digits or so. Trial division - or "baby divide," as some practitioners
term it - is useful for finding small factors of N.
There's trouble, however, if N is something like 2193 -
1. The smallest prime factor is a fairly accessible 13,821,503. The second
prime divisor of N lies somewhere in more distant parts. In fact,
if a computer could perform a billion division instructions per second, it
would require more than 35,000 years of computer time to find the second
largest factor of 2193 - 1. It took a new approach and considerable
effort by mathematicians Carl Pomerance and Samuel Wagstaff before they could
determine that N = 13,821,503 x 61,654,440,233,248,340,616,559
x 14,732,265,321,145,317,331,353,282,383 with each factor a prime.
At issue is whether a factoring method can be discovered that works efficiently
for any number. Clearly, trial division is good enough for factoring a large
number that happens to be the product of many small primes, but so far, a
200-digit composite that is the product of two 100-digit primes seems immune
to any known assault.
Two conflicting sentiments lie at the core of factoring theory and practice.
On the one hand, mathematicians would like to find new, faster algorithms
that would let them factor even larger numbers within a reasonable amount
of time. On the other hand, cryptographers who
have based the security of their systems on the presumed difficulty of factoring
want to be assured that really fast algorithms for factoring large, hard
numbers do not exist.
While conflict between these interests continues unresolved, factoring gets
steadily speedier. One important advance occurred in 1971, when John Brillhart
and Mike Morrison tried a roundabout rather than direct attack on factoring
a hard number. They looked for integers that could act as stand-ins for
N, the number to be factored. Their hope was that these substitutes
would be easier to handle yet would provide the necessary information to
flush out the primes of N.
The idea is to seek two numbers, x and y, that satisfy the
equation x2 - y2 = N. In other
words, a mathematician hoping to crack a hard composite must find two squares
whose difference is the number to be factored. A trivial example illustrates
the method. If N happens to be 24, then choosing x = 7 and
y = 5 meets the equation's requirements. Because x2 -
y2 can be factored algebraically into (x + y)
(x - y), then N must have the factors 12 and 2. Although
12 can be factored further, this method provides a good start on factoring
the number 24. The hard part is finding x and y, because random
dipping into the pool of available integers is about as futile as locating
two needles in a haystack.
What about a situation that requires locating thousands of needles in a haystack
that happens to contain millions? That sounds a little easier, especially
if the extra work provides a greater chance of success. In fact, mathematicians
have created just such a numerical haystack by breaking down the problem
of factoring one large number into the problem of factoring thousands of
smaller numbers that are relatively easy to manipulate. Because there are
millions of such numbers to choose from in any particular factoring problem,
the best strategy is to avoid wasting time on any small numbers that prove
to be uncooperative. A recalcitrant choice simply loses its place, and another
number steps in. That's the idea behind the quadratic-sieve and
continued-fraction methods, two of the most important general factoring methods
now in use.
The speed of factoring depends not only on the algorithm chosen, but also
on the type of computer used. Like the numerous ways in which partitions
may divide a building into hallways and rooms to channel movement from place
to place, a computer's architecture, built into its circuits and wiring,
controls the flow of data. Different computers shuffle digits in different
ways. Just because a path can be found from one place to another, whether
within a building or a circuit, doesn't mean that it's the most efficient
way to go.
Although buildings have movable interior walls and computers are programmable,
restrictions remain and bad fits may occur. For example, shoehorning a factoring
method such as the quadratic sieve into a given computer is sometimes akin
to asking a heart specialist to diagnose a foot ailment. It may take longer
than necessary for the answer to appear.
One solution to the problem of computers set in their ways is to select a
computer that seems to fit the chosen algorithm, then tinker with the algorithm
until it runs efficiently on that particular machine. For example, in the
computer version of the quadratic-sieve algorithm are extremely long strings
of digits. Such a string, also known as a vector, may have several thousand
components. During factoring, this vector is modified thousands of times,
but only a handful of digits change each time. Normally, no matter how few
digits are changed, the computer's processing time depends on the length
of the entire vector. A Cray supercomputer is designed, however, so that
changes can be made in specific vector components, and the time taken depends
only on the number of changes made, not on the vector's overall length. That
feature alone could improve quadratic sieving enormously.
In 1983, Gus Simmons, Jim Davis, and Diane Roldridge of the Sandia National
Laboratories implemented the quadratic-sieve algorithm on a Cray supercomputer.
Within months, their program was able to take on a 58-digit "most wanted"
number and vanquish it within 9 hours. Davis then worked out some modifications
to the algorithm that further quickened the factoring program, and soon after,
one "most wanted" number after another bit the dust.
Marv Wunderlich was able to speed up the continued-fraction factoring method
by tailoring it for a special computer called the Massively Parallel Processor,
an experimental computer at the NASA Goddard
Space Flight Center. This machine has 16,384 simple processors working like
a sharply coordinated drill team, so that each performs precisely the same
operation at the same time on different bits of data. Wunderlich and Hugh
Williams modified the continued fraction algorithm to take advantage of the
parallel processing available, especially for doing the huge number of trial
divisions the method requires. They also introduced features that allowed
the program to cut its losses early whenever it marched itself into an
unprofitable digital corner. The careful fitting of the continued-fraction
algorithm to the characteristics of the MPP added
10 digits to the size of numbers that could be factored in less than about
10 hours, bringing it closer in performance to the quadratic-sieving operation
on a supercomputer.
Curiously, the five or six best general-purpose factoring methods available
seem to share at least one feature. As a result of refinements, all of them
seem to have approximately the same theoretical upper limit on their running
times. Although such limits are not mathematically rigorous, they represent
reasonable estimates of how long a particular algorithm would take to do
its job. Whether that limit represents the true level of difficulty for factoring
integers isn't clear. No one seems to know what to make of this convergence.
The slow but steady progress in factoring hasn't been nearly as spectacular
as the advances in testing for primality. This may mean that factoring really
is a difficult problem for which no truly efficient algorithm can exist.
On the other hand, a brand new idea could jump the apparent barrier that
current methods seem to face. Mathematicians still seem to be a long way
from knowing how difficult factoring actually is.
