Quantum physics on the edge of chaos

Quantum physics describes the world of the very small. Classical Newtonian physics describes larger scales. But in the border country between the two, rigorous mathematical descriptions are difficult to find, and chaos rears its head.

MICHAEL BERRY

Before 1900, the foundation of physics was Newtonian mechanics. The main principle was that forces deflect objects according to laws that we can describe using simple mathematics. It was natural to think that because the laws are simple the motion of objects must be simple too. The spectacular success of classical mechanics in explaining regularities in the motion of the Moon and planets encouraged this view. It also inspired the invention of mechanisms imitating those regularities, such as clockwork.
This view is mistaken. Simple deterministic laws can generate very complicated and even random motion, because some systems are so unstable that the course of their trajectories depends sensitively on how they are started off. Even the motion of a billiard ball the archetypal Newtonian system can become complicated in certain simple systems. We can idealize the billiard ball as a point reflected elastically, in other words, without any loss of energy, from the boundary of the region in which it moves. Figure 15.1 shows what happens to the ball when we confine it in regions with different shapes. If the enclosure is a rectangle or a circle, the ball bounces round in a regular pattern. But if the boundary is shaped like a stadium or a bulgy Africa', then the ball bounces around chaotically, following no regular pattern at all.

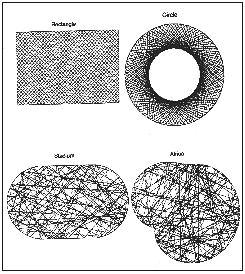Figure 15.1 The trajectory of a billiard ball depends on the shape of the boundary that confines it. In the rectangle and circle, the orbits are regular; in the stadium and Africa', they are chaotic.

Nowadays, the 'chaology' of classical mechanics is an intensively active area of research - chaology is a revival of a term used by theologians two centuries ago to mean the study of what existed before the Creation. It has applications ranging from the irregular tumbling of Saturn's satellite Hyperion to the intricate orbits of food particles in a liquidizer.
Since the 1920s, we have known that Newtonian mechanics, chaotic or not, is but an approximation to deeper truths about physics described by quantum mechanics. When dealing with objects and processes on atomic and smaller scales, it is quantum, not classical, theory that agrees with experiment. In its most familiar form, quantum mechanics is a wave theory. One consequence of this is that the energy of an isolated atomic system cannot take any value, as in classical physics. It is restricted to a set of possible energy levels. A common analogy is with a guitar string, on which waves have a discrete set of frequencies, or harmonics, that depend on the string's length, tension and density. The lowest energy corresponds to the ground state, in which the system usually exists. Higher energies correspond to excited states. Shining light of the appropriate frequency onto an atom will drive it into an excited state.
Quantum physics has its own randomness, to be sharply distinguished from any irregularity that Newtonian trajectories might possess. We cannot, for example, predict when a radioactive nucleus will decay, or where the next photon in a laser beam will strike a screen. But from the equations of quantum mechanics we can calculate with great accuracy the probabilities of these events from the intensities of the quantum waves. So quantum randomness lies not in the waves but in the processes the waves describe.
In the everyday world we can see, the direct effects of quantum mechanics are unobservably small because the wavelengths of the quantum waves are so small. Even for a bacterium, only a thousandth of a millimetre across, creeping at one millimetre an hour, the wavelength is a million times smaller than the bacterium itself - and 100 times smaller than an atom. On scales larger than an atom, we know that Newtonian mechanics works well, so that quantum mechanics must give the same predictions, in spite of its very different conceptual basis.
Niels Bohr, one of the pioneers of quantum physics, saw this relationship between Newtonian and quantum mechanics as a deep truth, which he called 'the correspondence principle'. Quantum mechanics must agree with Newtonian mechanics when applied to large or heavy systems - that is in the 'classical limit' where we can neglect wave effects. We are familiar with the principle applied to optics. Light is a wave, but, in explaining how cameras and telescopes work, it is useful to think in terms of well-defined rays, very similar to the trajectories of the particles, or 'corpuscles', Newton envisaged as the constituents of light.
We know that Newtonian physics can give rise to chaotic behaviour. According to the correspondence principle, quantum physics is identical to Newtonian physics in the classical limit. So how does the quantum system reflect this fact? What features of the way it evolves, and the way its energy levels are distributed, betray the irregularity of the Newtonian trajectories? Can quantum systems become chaotic as they approach the classical limit? These are questions of quantum chaology, an emerging science that is leading to the discovery of unfamiliar regimes of behaviour in microscopic systems.
The first surprise came 10 years ago, in a theoretical study by the Italian-Soviet-American collaboration of Giuho Casati at Milan, Boris Chirikov and Felix Izraelev at Novosibirsk, and Joseph Ford at Atlanta. They investigated how electrons in highly excited atoms - atoms with electrons in states of extremely high energy - absorb energy from radiation shining on them. To avoid tedious computations, necessary for real atoms containing many electrons, they thought of a simple idealized model of a circulating electron as a bead on a circular wire, endlessly pursuing its orbit (see Figure 15.2). The waves of radiation shining on the electron produce an oscillatory force. The researchers represented this as a sequence of impulses that provided a series of kicks to the 'bead'. The strength of the impulses depends on the position of the bead on the circle.
The orbits of this 'kicked rotator', when considered as a Newtonian system, can be regular or chaotic, depending on the strength of the impulses: stronger kicks give more chaos.

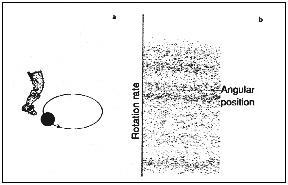Figure 15.2a The kicked rotator, an idealized model of an excited electron. Figure 15.2b The chaotic 'dust' generated by plotting angular position versus the rate of rotation after 5000 kicks.

Classical regularity is a steady state in which the rotator, on the average, gives back as much energy as it absorbs. We also find this behaviour when we carry out the quantum version of the 'experiment', by making the bead so light that we have to take into account its wavelength. Classical chaos, on the other hand, corresponds to erratic diffusion, with the rotator continuing to absorb energy at a rate which, on average, is constant.
In the chaotic case, however, the corresponding quantum rotator behaves differently (see Figure 15.3). For a while, the growth of the rotator's energy follows the classical straight line, but eventually, at a certain 'break-time', the energy begins to grow much more slowly, and may even decrease. This was a surprise. Quantum mechanics has suppressed the classical chaos. At first sight, it looks as though we have a conflict with the correspondence principle. But when we adjust the quantum model to make it more classical, for example by making the particle heavier, the break-time, which signals the onset of nonclassical effects, gets later and later. The theorists discovered this suppression of chaos by using a computer to solve the quantum equations numerically. After a decade of study, it is becoming clear that the suppression is a delicate and subtle wave-interference effect, but physicists have not yet worked this out in full detail.

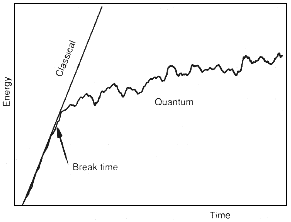Figure 15.3 After the 'break-time',the quantum rotator absorbs energy more slowly than the chaotic classical rotator.

A real atom differs from a model rotator in that an electron can become so excited as to leave the nucleus altogether -thus ionizing the atom. The probability that a given period of exposure to radiation of a certain frequency will result in ionization depends on the intensity of the radiation and how excited the atom is to start with. These conditions determine whether the classical electron trajectories are chaotic or regular, and whether the probabilities of ionization calculated using the classical approximation are the same as those calculated by the more accurate laws of quantum mechanics.
Physicists have carried out experiments on hydrogen atoms illuminated with microwaves in classically chaotic regimes for which classical and quantum predictions agree - that is before the break-time. They were surprised to find systems as small as atoms behaving classically. Remember the absorption and emission of photons by atoms is a highly non-classical process. The pattern of emission and absorption lines in a spectrum was one of the observations that led to the discovery of quantum mechanics.
The difference between the new spectroscopy and the old is that the new experiments employ intense radiation, and the atoms are in highly excited states to start with, so they absorb and emit large numbers of photons, rather than one or two. Theory predicts that, as with the rotator, quantum mechanics will eventually suppress classical chaos. Experiments to test this important effect would require that we measure the ionization after much longer periods of illumination. This is technically difficult and, so far, no one has managed to do it.
Now we turn to the quantum chaology of systems that are either isolated or else are influenced by external forces that do not vary - in contrast to the oscillatory force of radiation just considered. The energy levels of such systems describe their quantum states. It turns out that the distribution of highly excited quantized energy levels - the pattern of notes of the harmonics on the musical analogy - depends in a fundamental way on whether the trajectories of the corresponding classical system are regular or chaotic.

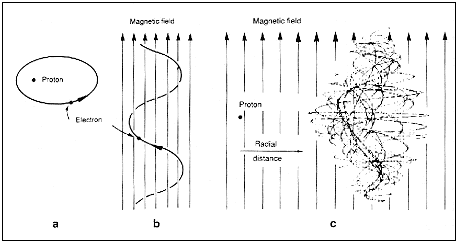Figure 15.4 Electron orbits: a, regular motion in the field of a proton alone; b, regular motion in a magnetic field alone; C, chaotic motion in a combined field.

A system encompassing both extremes is the single electron of a hydrogen atom in a very strong magnetic field - for example, the magnetic field in a white dwarf star, which can be a billion times greater than the Earth's field. At low energies, the nucleus of the hydrogen atom, the proton, binds its electron tightly. The electrostatic force between the proton and the electron completely dominates the magnetic force. The classical orbits are ellipses (see Figure 15.4) like the paths of planets round the Sun, and there is no chaos. At very high energies, the electron is far from the nucleus and now it is the magnetic force that dominates. The orbits are helices spiralling round the lines of the magnetic field, and again there is no chaos. At intermediate energies, however, the two forces are comparable but exert contrary influences. The classical electron resolves the contradiction by moving chaotically.
For the electrons behaving in a quantum fashion, we have to compare the distributions of large numbers of excited energy levels in the regular and chaotic regimes. One way to do this is by computing the statistics of the levels. One convenient statistic is the spacings between neighbouring levels, calculated at low and intermediate energies in the atom's spectrum of energy levels. If the levels are regularly arranged, like the rungs of a ladder, the distribution of spacings will cluster about the average spacing, producing a curve like that in Figure 15.5a. You would get a similar distribution by plotting the heights of a group of people. In this case there are few small spacings - it is as though the levels repel each other. If, on the other hand, the levels are randomly distributed - that is, uncorrelated, like the arrival times of raindrops in a shower - the distribution of spacings will be broad, with a preponderance of small spacings. The surprise this time was the discovery that the levels are more regularly arranged when the classical orbits are chaotic (see Figure 15.5a), and randomly distributed when the orbits are regular (see Figure 15.5b). Experiments on magnetized hydrogen confirm even the fine details of the theoretically calculated spectrum.

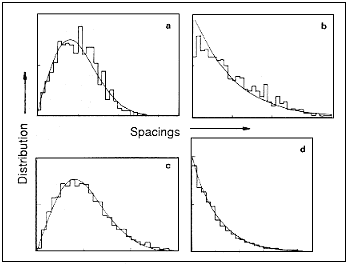Figure 15.5 The distribution of spacings between neighbouring energy levels: a, hydrogen in a magnetic field with chaotic classical orbits showing repulsion of levels; b, hydrogen in a magnetic field with regular classical orbits showing clustering of levels; C, the energy levels for quantum billiards in a stadium; d, the energy levels for quantum billiards in a rectangle.

This behaviour is not just a peculiarity of the magnetized hydrogen atom. On the contrary, the spacings of the quantum energy levels always depend only on whether the classical orbits are chaotic or regular and not on any other details of the system. To illustrate this, Figure 15.5 also shows the distributions of the spacings of energy levels for the quantized versions of two of the billiard ball games in Figure 15.1. The stadium game is classically chaotic but has regular spacings of its quantum levels (see Figure 15.5c), while the rectangle game is classically regular but has random spacings of its quantum levels corresponding to chaotic motion. These tend to repel one another. Quantum billiards might appear to be an exotic creation of theorists, far removed from reality, but exactly the same mathematics describes the frequencies of a vibrating membrane shaped like the billiard table. In the three-dimensional version, it also describes the acoustics of a concert hall.
The repulsion of levels in Figures 15.5b and 15.5d is not the most general quantum signature of classical chaos, because all systems so far discussed have a special feature, namely symmetry. The atom in a magnetic field has the symmetry of a cylinder, and the movement of the billiards is symmetrical with respect to time, in the sense that, if at any instant the velocity of the moving billiard ball reverses, it will retrace its previous path. When there is no symmetry of any kind and the classical orbits are chaotic a combination of circumstances still out of range of experiment -theory predicts that repulsion between the levels remains but it is of the slightly stronger kind shown in Figure 1 5.6a, in which the slope of the curve vanishes at zero spacing - the curve flattens out. This particular calculation was for the energies of a charged quantum particle moving in the 'Africa' billiard table of Figure 15.1 with a magnetic field acting at right angles to the plane, but it represents quantum chaology in the most general case.

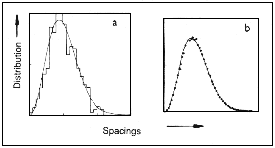Figure 15.6 The distribution of spacings where there is no symmetry: a, several hundred energy levels of the 'Africa' game of quantum billiards in a magnetic field; b,100 000 zeros of Reimann's zeta function.

At this point, quantum chaology makes unexpected contact with one of the long-standing problems of pure mathematics, namely the Reimann hypothesis of number theory. In 1859, Georg Bernhard Reimann - a German mathematician who also developed the study of geometry to include that with more than three dimensions - was studying the distribution of prime numbers. He devised a quantity, which he called the zeta function, whose value depends on position in a plane of complex numbers. Complex numbers (denoted by s) have a 'real' part and an 'imaginary' part involving the square root of minus 1. The x axis represents real numbers and the y axis imaginary numbers. Reimann's function was the extension to the whole s plane of

zeta (s)= 1 +¹/₂^s+ ¹/₃^s+...

His famous hypothesis was that the points at which the zeta function vanishes - its zeros - lie on the straight line with x =1/2. (If the hypothesis were true, certain theorems about prime numbers would follow.) Numerical studies have shown that the first 1 500000000 zeros lie on Reimann's line, but nobody has been able to prove that they all do (see Figure 15.7).

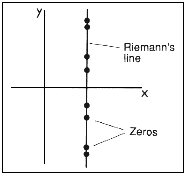Figure 15.7 The plane is inhabited by Reimann's zeta function.His hypothesis is that the function's zeros lie on the line shown.

The connection with quantum chaology comes in calculations by Andrew Odlyzko (AT & T Bell Laboratories, New Jersey) of the distribution of the spacings between neighbouring zeros; this takes 20 hours of Cray supercomputer time and results in the graph in Figure 15.6. It is not just the evident similarity between Figures 1 5.6a and 1 5.6b, but also a variety of other evidence, which suggests that underlying Reimann's zeta function is some unknown classical, mechanical system whose trajectories are chaotic and without symmetry, with the property that, when quantized, its allowed energies are the Reimann zeros. These connections between the seemingly disparate worlds of quantum mechanics and number theory are tantalizing.
The phenomena of quantum chaology lie in the largely unexplored border country between quantum and classical mechanics; they are part of semiclassical mechanics. This is an area where rigorous mathematical development, as employed elsewhere in mechanics, is difficult. Most discoveries have been made by computer experiments with the quantum equations, guided by intuition and analogy. As the subject matures we can expect, on the one hand, more experiments on real physical systems, and, on the other, the precise formulation and proof of mathematical theorems.

New Scientist  28 Oct 1989 File Info: Created 16/7/2013 Updated 10/9/2017 Page Address: http://leebor2.100webspace.net/Zymic/edgechaos.html