 |
Duncan Graham-Rowe
Astronomers are taking the search for somewhere quiet to work
to new extremes with a plan to put a radio telescope on the far side of the
Moon. The advantage of this unusual location is that the
Moon would act as a massive shield, protecting the telescope against
radio emissions from Earth. Astronomers could also listen to low radio
frequencies that don't penetrate the Earth's atmosphere. Claudio Maccone,
an astronomer at the Centre for Astrodynamics in Turin, Italy, is assessing
the concept for the International Academy of Astronautics. He even has his
eye on a plot of lunar real estate. A 100-kilometre-wide crater called
Daedalus should provide enough space, he says. The crater's
3-kilometre-high rim should also help block any stray radio signals that
creep around the Moon to the far side. "I do believe this will be built,"
says Maccone, although he admits it will probably take at least 15 years.
Even if robots were used to build the observatory remotely, it would cost
billions of dollars and need the backing of a large space agency like NASA
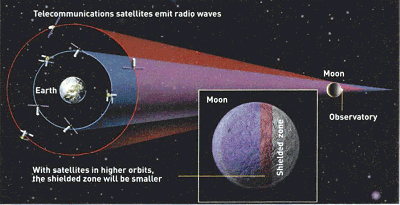
or the European Space Agency. By the time the telescope could be built, the
area of the Moon that's protected from radio waves is likely to be shrinking
fast. This is because as orbit space for telecommunications satellites gets
used up, they will have to be placed in higher orbits, so their radio emissions
will reach more and more of the Moon's surface (see Graphic). So Maccone
also wants to give the region around the Daedalus crater some form of protection
status, to create a permanent quiet zone that would be safe no matter what
technology is developed in the future. "The far side is in my opinion a unique
treasure that should be preserved for the sake of humankind," he says. Setting
up such a zone would probably be the responsibility of the International
Telecommunications Union, which allocates the rights to use different radio
frequencies. But it's far from clear whose permission would be needed to
build a permanent structure on
the Moon. Maccone is
due to present the results of his study to the International Astronautical
Congress next October. If the plans are approved, the first step will be
to design a satellite probe to orbit the Moon and check there really is a
quiet zone.
Jupiter's giant light show |
 SOMETHING
strange is happening on Jupiter. Its magnetic field extends hundreds of times
further out into space than previously thought, creating auroras that make
the Earth's northern lights seem feeble in comparison. Jupiter is the giant
of the Solar System, more than a thousand times as massive as Earth. In January
2001, the combined power of the Cassini and Galileo space probes, the Chandra
X-ray telescope and the Hubble Space Telescope were all trained on the Jovian
magnetosphere - the region controlled by the planet's magnetic field. Magnetic
field lines fan out from a planet like the lines of iron filings from the
poles of a bar magnet. Auroras are caused by ions zipping along these lines,
so researchers can use the location of auroras to track how far out into
space the planet's magnetic field lines can trap ions from the solar wind. SOMETHING
strange is happening on Jupiter. Its magnetic field extends hundreds of times
further out into space than previously thought, creating auroras that make
the Earth's northern lights seem feeble in comparison. Jupiter is the giant
of the Solar System, more than a thousand times as massive as Earth. In January
2001, the combined power of the Cassini and Galileo space probes, the Chandra
X-ray telescope and the Hubble Space Telescope were all trained on the Jovian
magnetosphere - the region controlled by the planet's magnetic field. Magnetic
field lines fan out from a planet like the lines of iron filings from the
poles of a bar magnet. Auroras are caused by ions zipping along these lines,
so researchers can use the location of auroras to track how far out into
space the planet's magnetic field lines can trap ions from the solar wind.
Randy Gladstone and his colleagues at the Southwest Research Institute in San Antonio, Texas, used Chandra to map the Jovian auroras. Earth's northern lights shine only with visible light, but the more violent Jovian auroras emit X-rays. The X-ray auroras on Jupiter extend surprisingly far from the planet's poles, showing that field lines reach far out into space. Gladstone also found that the auroras pulsated regularly every 45 minutes in certain places he's calling "hot spots", unlike anything seen on Earth. "Those field lines go way further out than expected," says Gladstone. "Something weird is happening." Theorists have trouble explaining why Jupiter's magnetosphere is so much more powerful than Earth's, even allowing for the planet's greater size. "Jupiter's magnetosphere is like Earth's on steroids," says Thomas Hill, who works on the theory of magnetospheres at Rice University in Houston, Texas. Eugenie Samuel, Boston More at. Nature (vol 415, p 1000) [New Scientist 2 March 2002]
|
Mercury and the mystery of a "planet" that disappeared |
| Experience has taught me that predictions
of spectacular astronomical events are tantamount to long-range
forecasts of bad
weather: the grand alignment of five planets scheduled
to take place over the western horizon tomorrow evening therefore means that
gardeners should put any house plants needing a watering outside at about
8pm. The various planets, fortunately, will be dancing around each other in the same part of the sky for a few weeks, so I still hope for a glimpse of Mercury, the one planet visible to the naked eye that I have yet to see. Tomorrow's planetary alignment will form a vast celestial finger pointing to its location at the bottom of a line that baa Jupiter at its top, followed by Saturn, Mars and Venus, with the Moon just below the Red Planet. One consequence of Mercury's elusiveness is that astronomers know little about this planet. Data sent back by the only space probe to visit it, Mariner 10 in 1974, raised as many mysteries as it solved. The mass of the planet turned out to be extraordinarily high: despite being not much larger than the Moon, Mercury proved to be five times more massive - suggesting that its rocky, cratered surface covers a colossal nickel-iron ball more than 2,000 miles across. The planet also has a relatively strong magnetic field, thus cocking a snook at scientists who claim to know how such fields are generated. Standard theories link them to the spin of the planets, which creates a kind of dynamo effect within electrically conducting liquid cores. Mercury's metal core is certainly conducting, but it isn't liquid and the planet takes a leisurely 58 days to spin once on its axis (which, mysteriously, is precisely two thirds the time Mercury takes to orbit the Sun). The answers to such puzzles almost certainly lie in the proximity of Mercury to the Sun. There is no object' however, similar to Mercury hy which astronomers can test their theories. Not that this has prevented some of the more imaginative from suggesting that Mercury may not be the only object to inhabit the searing inner reaches of our solar system. During the 1840s, astronomers were struggling to understand Mercury's slow pirouettes around the Sun. Most of the rotation could be explained by known effects, but a tiny discrepancy remained. The mystery was tackled by Urbain Leverrier, the brilliant French theoretician who had in 1846 explained discrepancies in the orbit of Uranus as being due to an undiscovered planet, subsequently confirmed as Neptune. In 1859 Leverrier proposed that Mercury was being pulled off course by another undiscovered planet, duly named Vulcan. Shortly afterwards, Leverrier received a letter from a French country doctor claiming to have seen Vulcan crossing the face of the Sun in March 1859. Calculating an orbit for the object, Laverrier found that it must lie just 13 million miles from the Sun. This neatly explained why no one had seen it: Vulcan was even smaller than Mercury and would normally be lost in the Sun's glare. Not unreasonably, Leverrier went to his grave believing he had predicted the existence of two new planets. He proved to be only half right. Vulcan was never seen again, and the real explanation for Mercury's anomalous orbit turned out to be general relativistic effects unimagined in Leverrier's time. Vulcan may now reside in the wastebin of scientific history, but it is odd that the early claims to have seen it should have been so consistent. That said, readers who think they see Vulcan over the weeks ahead should probably take it as a reminder to have an eye test. [Sunday Telegraph April 14 2002] Robert Matthews invites you to send. in your questions on science, the answer's to which will soon form a regular part of his column whether you're stumped by celestial mechanics or just want to know why the sea is salty, please write to Robert Matthews at The Sunday Telegraph, 1 Canada Square, London, E14 5DT, or e-mail: robert.matthews@telegraph.co.uk |
| The zodiac
can at times appear predominantly masculine as most of the planets have
historically been associated with male mythological figures. Until the discovery
of the asteroid belt in the 19th century, the only planetary bodies which
women could easily identify themselves with were
Venus, the Moon and Lilith (which is considered to be Earth's ante-diluvian
satellite). While women have always made significant contributions to society, it must be stressed that they traditionally played the roles of wife and mother as illustrated by Venus and the Moon respectively. The discovery of the asteroid belt brought about a balance between masculine and feminine archetypes to bring more sexual equality in our Solar system. It was also around this time that women began to take on more diversified roles and therefore needed other astrological indicators in what was to become a rapidly changing world. It is also worth noting that those men who have chosen to pursue careers which have traditionally been assigned to women will be able to relate to these more intuitive planetary bodies. The Moon The Moon is the Earth's largest satellite which governs our emotional responses. It is no secret that the close proximity of the Moon to the Earth has a strong effect on our physical environment, as evidenced by the daily motion of oceanic tides and the fact that crime has a tendency to increase during the Full Moon. The Moon relates to our emotive impulses which push us to react and in many instances it can be such a dominant feature in some horoscopes that it is actually more prominent than the Sun. This may be, as many whose natal Moon is strongly aspected in their natal chart will find to be the case, the reason why some do not show a strong affinity to their natal Sun but instead relate more to Lunar impressions. The Moon represents the relationship we have with our mother and women in general and it denotes what type of mother or parent we are likely to become. While the father is quite often associated with Saturn, those men who are more in tune with the intuitive side of themselves can just as easily identify with the Moon in relation to their parenting style. In Greek mythology, the Moon is associated with Artemis, the virgin goddess. She was considered to be eternally young and active and was equal to any man. Artemis was the twin sister of Apollo who astrologically depicts the Sun and the pair were said to have been very close. With these mythological considerations in mind, it should come as no surprise to conclude that the astrological signs of Leo and Cancer, ruled by the Sun and Moon respectively, reign side by side in the zodiac while the remaining five planets in the ancient Solar system progress outwardly from the royal pair. The planetary alignment is as follows: Mercury, the first planet away from the Sun, rules Gemini and Virgo which are one sign away from the Cancer/Leo configuration respectively. Venus, the second planet away from the Sun, rules Taurus and Libra which are two signs away from the Cancer/Leo configuration respectively. Mars, the third planet from the Sun excluding Earth, rules Aries and Scorpio which are three signs away from the Cancer/Leo configuration respectively. Jupiter, the fourth planet from the Sun excluding Earth, rules Pisces and Sagittarius which are four signs away from the Cancer/Leo configuration respectively. Saturn, the fifth planet from the Sun excluding Earth, rules Capricorn and Aquarius which are five signs away from the Cancer/Leo configuration respectively. The placement of these signs and the rulerships they were given some 2,000 years ago does seem to suggest that the Summer months were regarded as significant in the astrological year.[Predictions magazine July 1997] |
 Question: What is a blue moon and what is once in a blue moon?
The three most popular reasons that are most often found in the literature
for this so called phenomena are 1) The appearance of the moon's color due
to smoke particles from forest fires, 2) The appearance of the moon's color
due to particles from volcanic eruptions, or 3) The appearance of a second
full moon within a calendar month. Apparently, both 1 and 2 have been known
to give the moon a blue appearance. The third is the source of the popular
statement "once in a blue moon" which means something happens quite rarely.
It is based on the strange occurrence of having two full moons in one month.
How can this happen? Since full moons actually occur every about 29.53 days,
they occur about 12.36 times a year, which translates into having a double
full moon month once every 2.77 years or so, quite infrequently, obviously.
With the event occurring approximately every 33 months, it is easy to see
how the statement "once in a blue moon" could have originated. It might also
just be the case that some specific second full moons in months past did,
in fact, occur right after a forest fire or volcanic eruption, providing
some credibility to all three. It is interesting to note that in a year where
a full moon does not occur in February, both January and March will have
two full moons, a rare event indeed. Question: What is a blue moon and what is once in a blue moon?
The three most popular reasons that are most often found in the literature
for this so called phenomena are 1) The appearance of the moon's color due
to smoke particles from forest fires, 2) The appearance of the moon's color
due to particles from volcanic eruptions, or 3) The appearance of a second
full moon within a calendar month. Apparently, both 1 and 2 have been known
to give the moon a blue appearance. The third is the source of the popular
statement "once in a blue moon" which means something happens quite rarely.
It is based on the strange occurrence of having two full moons in one month.
How can this happen? Since full moons actually occur every about 29.53 days,
they occur about 12.36 times a year, which translates into having a double
full moon month once every 2.77 years or so, quite infrequently, obviously.
With the event occurring approximately every 33 months, it is easy to see
how the statement "once in a blue moon" could have originated. It might also
just be the case that some specific second full moons in months past did,
in fact, occur right after a forest fire or volcanic eruption, providing
some credibility to all three. It is interesting to note that in a year where
a full moon does not occur in February, both January and March will have
two full moons, a rare event indeed. Prepared by AACTchWill and AACTutorNY, AAC Staff, Use of this material is protected under America Online and other copyright. Any use of this material must cite AOL's Academic Assistance Center and the authors as a source. (edited by AACDrAnne) |
The Golden age of Brum
John Adamson praises the elegant study of the friends who
meet once a month to change the world [The Lunar Men:The Friends who
made the future by Jenny Uglow Faber £25,518pp] |
| DEEP SPACE SECRETS Over 130 molecules have been identified
in interstellar space so far, including sugars and ethanol. Now Lewis Snyder
and Yi-Jehng Kuan of the National Taiwan University say they have spotted
the amino acid glycine. Amino acids in deep space are a particularly important
discovery because they link up to form proteins. If the finding stands up
to scrutiny it will add oomph to ideas that life exists on other planets,
and even that molecules from outer space kick-started life on Earth. FEEL THE FORCE Pioneer 10 was the first spacecraft to fly past Jupiter. Pioneer 11 went on to visit Saturn. Out at the darkest edge of the Solar System beyond Pluto, there should be nothing to slow the probes down except the feeble gravity of the receding Sun - yet a mysterious extra force seems to be tugging on them. "For the life of me, I can't think what it could be," says Michael Martin Nieto from Los Alamos National Laboratory in New Mexico. But "I admit I want it to be something profoundly important, some entirely new physics," he adds. And he just may be in luck... |
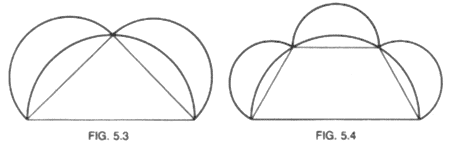
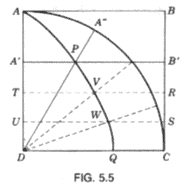
| QUADRATURE OF LUNES Somewhat younger than Anaxagoras, and coming originally from about the same part of the Greek world, was Hippocrates of Chios. He should not be confused with his still more celebrated contemporary, the physician Hippocrates of Cos. Both Cos and Chios are islands in the Dodecanese group; but Hippocrates of Chios in about 430 B.C. left his native land for Athens in his capacity as a merchant. Aristotle reports that Hippocrates was less shrewd than Thales and that he lost his money in Byzantium through fraud; others say that he was beset by pirates. In any case, the incident was never regretted by the victim, for he counted this his good fortune in that as a consequence he turned to the study of geometry, in which he achieved remarkable success-a story typical of the Heroic Age. Proclus wrote that Hippocrates composed an "Elements of Geometry," anticipating by more than a century the better-known Elements of Euclid. However, the textbook of Hippocrates-as well as another reported to have been written by Leon, a later associate of the Platonic school-has been lost, although it was known to Aristotle. In fact, no mathematical treatise from the fifth century has survived; but we do have a fragment concerning Hippocrates which Simplicius (fi.. ca. 520) claims to have copied literally from the History of Mathematics (now lost) by Eudemus. This brief statement, the nearest thing we have to an original source on the mathematics of the time, describes a portion of the work of Hippocrates dealing with the quadrature of lunes. A lune is a figure bounded by two circular arcs of unequal radii; the problem of the quadrature of lunes undoubtedly arose from that of squaring the circle. The Eudemian fragment attributes to Hippocrates the following theorem: Similar segments of circles are in the same ratio as the squares on their bases. The Eudemian account reports that Hippocrates demonstrated this by first showing that the areas of two circles are to each other as the squares on their diameters. Here Hippocrates adopted the language and concept of proportion which played so large a role in Pythagorean thought. In fact, it is thought by some that Hippocrates became a Pythagorean. The Pythagorean school in Croton had been suppressed (possibly because of its secrecy, perhaps because of its conservative political tendencies), but the scattering of its adherents throughout the Greek world served only to broaden the influence of the school. This influence undoubtedly was felt, directly or indirectly, by Hippocrates. The theorem of Hippocrates on the areas of circles seems to be the earliest precise statement on curvilinear mensuration in the Greek world. Eudemus believed that Hippocrates gave a proof of the theorem, but a rigorous demonstration at that time (say about 430 B.C.) would appear to be unlikely. The theory of proportions at that stage probably was established for commensurable magnitudes only. The proof as given in Euclid XII.2 comes from Eudoxus, a man who lived halfway between Hippocrates and Euclid. However, just as much of the material in the first two books of Euclid seems to stem from the Pythagoreans, so it would appear reasonable to assume that the formulations, at least, of much of Books III and IV of the Elements came from the work of Hippocrates. Moreover, if Hippocrates did give a demonstration of this theorem on the areas of circles, he may have been responsible for the introduction into mathematics of the indirect method of proof. That is, the ratio of the areas of two circles is equal to the ratio of the squares on the diameters or it is not. By a reductio ad absurdum from the second of the two possibilities, the proof of the only alternative is established. From this theorem on the areas of circles Hippocrates readily found the first rigorous quadrature of a curvilinear area in the history of mathematics. He began with a semicircle circumscribed about an isosceles right triangle, and on the base (hypotenuse) he constructed a segment similar to the circular segments on the sides of the right triangle. (Fig. 5.1). Because the segments are to each other as squares on their bases, and from the Pythagorean theorem as applied to the right triangle, the sum of the two small circular segments is equal to the larger circular segment. Hence, the difference between the semicircle on AC and the segment ADCE equals triangle ABC. Therefore, the lune ABCD is precisely equal to triangle ABC; and since triangle ABC is equal to the square on half of AC, the quadrature of the lune has been found. 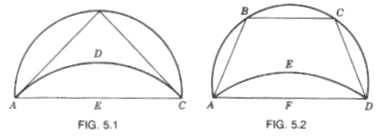 Eudemus describes also an Hippocratean lune quadrature based on an
isosceles trapezoid ABCD inscribed in a circle so that the square on the
longest side (base) AD is equal to the sum of the squares on the three equal
shorter sides AB and BC and CD (Fig. 5.2). Then, if on side AD one constructs
a circular segment AEDF similar to those en the three equal sides, lune ABCDE
is equal to trapezoid ABCDF. Eudemus describes also an Hippocratean lune quadrature based on an
isosceles trapezoid ABCD inscribed in a circle so that the square on the
longest side (base) AD is equal to the sum of the squares on the three equal
shorter sides AB and BC and CD (Fig. 5.2). Then, if on side AD one constructs
a circular segment AEDF similar to those en the three equal sides, lune ABCDE
is equal to trapezoid ABCDF.That we are on relatively firm ground historically in describing the quadrature of lunes by Hippocrates is indicated by the fact that scholars other than Simplicius also refer to this work. Simplicius lived in the sixth century, but he depended not only on Eudemus (fi. ca. 320 B.C.) but also on Alexander of Aphrodisias (fi. ca. A.D. 200), one of the chief commentators on Aristotle. Alexander describes two quadratures other than those given above. (1) If on the hypotenuse and sides of an isosceles right triangle one constructs semicirdes (Fig. 5.3),then the lunes created on the smaller sides together equal the triangle. (2) If on a diameter of a semicircle one constructs an isosceles trapezoid with three equal sides (Fig. 5.4), and if on the three equal sides semicircles are constructed, then the trapezoid is equal in area to the sum of four curvilinear areas: the three equal lunes and a semicircle on one of the equal sides of the trapezoid. From the second of these quadratures it would follow that if the lunes can be squared, the semicircle-hence the circle-can also be squared. This conclusion seems to have encouraged Hippocrates, as well as his contemporaries and early successors, to hope that ultimately the circle would be squared.
CONTINUED PROPORTIONS
HIPPIAS OF ELIS |

The Pink "pirate" who sailed the southern starsComet man Halley also blazed a trail on Earth in a search for Antarctica |
||||
| ONE day in l700 a fishing vessel was at
work off the Newfoundland coast when a ragged looking craft bore down
on it. Fearing piracy, the fisherman opened fire. The result was a torrent
of foul language from the "pirate's" commander, the astronomer Edmond Halley.
Halley was not only famous for predicting the appearance of his comet. He was also a bold explorer, travelling the world in search of scientific information, who nearly lost his life trying to find Antarctica a century before Captain Cook arrived. His extraordinary exploits are revealed in the latest issue of Astronomy Now by the scientific historian Dr Ian Seymour, who relates that Halley was not only a precursor of Cook but, in being faced with a mutiny that he himself partly provoked, of Captain Bligh too. In his second voyage, begun in 1698, he set out in a Royal Naval vessel called the Paramour Pink.  "Pinks", flat-bottomed ships 52 feet long and 18 feet broad,
-specially designed for sailing in shallow seas and almost unknown in the
Navy, were often mistaken for pirates sailing under false colours. "Pinks", flat-bottomed ships 52 feet long and 18 feet broad,
-specially designed for sailing in shallow seas and almost unknown in the
Navy, were often mistaken for pirates sailing under false colours.The crew numbered 20, making the vessel extremely cramped, and the first officer, a certain Harrison (no relation to the inventor of the marine chronometer) was a professional seaman who despised the "academic" Halley from whom, he complained with gross unfairness, "much is expected and little or nothing appears". During this voyage Halley did in fact make extensive observations of the Earth's magnetic fields which, Dr Seymour says, "remained indispensable shipboard companions for more than a century". But he was an appallingly bad commander. Despite his naval authority, he never had a man flogged and attempted to enforce discipline with sarcastic and foul-mouthed abuse. Harrison, openly insubordinate, countermanded orders and told the crew that Halley had only been given command because of his wealthy connections, since he was useless for any other occupation. One day Harrison told Halley in the presence of all the crew that he was "not only uncapable to take charge of a Pink, but even of a longboat". Halley had him confined to his cabin for the rest of the voyage. At the subsequent court martial the Admiralty appeared to recognise Halley's faults, for the mutinous officer escaped with only a reprimand. On a subsequent voyage in a Pink, this time with a more agreeable first officer, Halley put in at Recife, Brazil, where he fell foul of the English consul, a Mr Hardwicke; whom he afterwards alleged was an imposter. He told Hardwicke that the purpose of the voyage was to observe the stars in the southern skies. (Halley, in fact, had earlier won election to the Royal Society for identifying 341 southern stars from the murky skies of Saint Helena.)
Hardwicke said this story was too ridiculous to be believed.
Citing the suspicious appearance of Halley's ship, he ordered him to be arrested
as a pirate. Halley was released after a few hours at the intervention of
the city's governor but,incensed and refusing to accept apologies, he set
off into stormy seas.
|

The Sun | The Solar System | The Sky at Night | Moonshadow's Realm
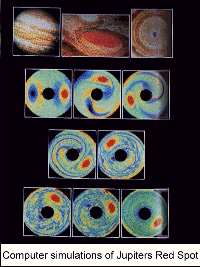 HOW JUPITER GOT
ITS STRIPES. A new study of turbulence in the atmosphere around a rotating
sphere is helping to explain the dramatic stripes on Jupiter, Saturn, and
the other giant planets. On Earth, turbulence caused by solar heating and
friction with the ground disrupts atmospheric flows and dissipates the energy
provided by the sun that might otherwise lead to the formation of circulating,
global cloud bands. In the thin atmospheres of gas giants, however, energy
dissipation is small, and some of the sun's energy is gradually collected
in stable, global jets that trap clouds and form planetary stripes. Researchers
at the University of South Florida and Ben-Gurion University of the Negev
(Israel) have now developed a model that shows how planetary rotation and
nearly two-dimensional atmospheric turbulence may combine to create large
scale structures. Scientists have long suspected that the interaction between
planetary rotation and large-scale turbulence governs the banded circulations
on giant planets. The new research has quantified the phenomenon, leading
to an equation that characterizes the distribution of energy among different
scales of motion, and to simple formulae that describe basic energetic features
of giant planets' circulations. The model helps explain the paradoxical
observation that the outer planets have stronger atmospheric flows, even
though the energy provided by the sun to maintain such flows decreases with
increasing distance from the sun. The researchers (B. Galperin,
bgalperin@marine.usf.edu, 727-553-1101) have found that the atmospheres of
distant planets dissipate even less energy than their warmer sisters. Although
the outer planets receive less energy from the sun, they keep more of the
energy they receive. As a result, the model shows why Neptune has the strongest
atmospheric circulation of all the gas giants even though it is the farthest
of the bunch from the sun. (S. Sukoriansky, B. Galperin, N. Dikovskaya, Physical
Review Letters, 16 September 2002)
HOW JUPITER GOT
ITS STRIPES. A new study of turbulence in the atmosphere around a rotating
sphere is helping to explain the dramatic stripes on Jupiter, Saturn, and
the other giant planets. On Earth, turbulence caused by solar heating and
friction with the ground disrupts atmospheric flows and dissipates the energy
provided by the sun that might otherwise lead to the formation of circulating,
global cloud bands. In the thin atmospheres of gas giants, however, energy
dissipation is small, and some of the sun's energy is gradually collected
in stable, global jets that trap clouds and form planetary stripes. Researchers
at the University of South Florida and Ben-Gurion University of the Negev
(Israel) have now developed a model that shows how planetary rotation and
nearly two-dimensional atmospheric turbulence may combine to create large
scale structures. Scientists have long suspected that the interaction between
planetary rotation and large-scale turbulence governs the banded circulations
on giant planets. The new research has quantified the phenomenon, leading
to an equation that characterizes the distribution of energy among different
scales of motion, and to simple formulae that describe basic energetic features
of giant planets' circulations. The model helps explain the paradoxical
observation that the outer planets have stronger atmospheric flows, even
though the energy provided by the sun to maintain such flows decreases with
increasing distance from the sun. The researchers (B. Galperin,
bgalperin@marine.usf.edu, 727-553-1101) have found that the atmospheres of
distant planets dissipate even less energy than their warmer sisters. Although
the outer planets receive less energy from the sun, they keep more of the
energy they receive. As a result, the model shows why Neptune has the strongest
atmospheric circulation of all the gas giants even though it is the farthest
of the bunch from the sun. (S. Sukoriansky, B. Galperin, N. Dikovskaya, Physical
Review Letters, 16 September 2002) 

 Surrounded
by these icebergs and by thick fog, the ship was soon in deadly peril. For
"between 11 and 12 days", Halley wrote in the log, "we were in imminent danger
of the inevitable loss of all of us in case we starved, being alone without
a consort". They were saved by the smallness of the ship, which made it
responsive to controls, and by its shallow draft.
Surrounded
by these icebergs and by thick fog, the ship was soon in deadly peril. For
"between 11 and 12 days", Halley wrote in the log, "we were in imminent danger
of the inevitable loss of all of us in case we starved, being alone without
a consort". They were saved by the smallness of the ship, which made it
responsive to controls, and by its shallow draft.
