

by Ian Stewart
Fibonacci Forgeries
"A toast,ladies and gentleman: To the queen!" We stood dutifully,raised
our glasses and murmured the sovreigns name.It should have been a poignant
moment,but it was spoiled by the person next to me,who flopped back into
his chair and muttered, "Thank God,now I can smoke!" (It is a quaint British
custom that at a formal dinner,no one may smoke before the party drinks to
the queen's health.)
"I'd rather you didn't," I said,"I'm a nonsmoker".
"You had the smoked salmon," he said and roared with laughter as he lit a
cigarette. I wrinkled my nose and glanced at his badge: Richard Byrd. He
had pencilled in "Call me Dicky".
"The salmon,by the way,was terrible," I told him., "In fact I think it was
really dogfish dyed orange".
He did not look surprised.The annual dinner of CAT-DOG (The Charitable
Association for the Tax-Deductible Offerings of Generosity) was always a
disaster.
"I wondered why the fish was wearing a flea collar," said the lady on my
left. I had met her at other gatherings: Amanda Bander-Gander,a leading light
of the local Animal Protection Society.
"No,dear,you just dropped your napkin ring on it," her husband yelled from
five places down on the opposite side of the table. Alexander Bander-Gander,a
lawyer,was sandwiched between Althanisius Fell,a doctor and Dennis Racket,an
old friend of mine from the tennis club. "So what business are you in?" Dicky
asked me. I leaned closer to him and whispered "I'm a mathematician".
As usual,though I had spoken below the threshold of aural perception,it was
a party stopper.The entire table went silent. "I
was never - " he began, "any good at maths at school," I finished, "That's
what they all say".
"Hated it then," Athanasius mumbled, "Still do". "I must be the exception!",a
voice boomed to my right. "Absolutely loved it!Name's Adam Smasher.I'm a
nuclear physicist. I have a little puzzle I'll
ask you.What's the next number in the sequence
1,1,2,3,5,8,13,21?"
"Nineteen," I grunted
automatically,while battling with a bread roll seemingly baked with cement.
"You're not supposed to answer," he said."Anyway,you're wrong - it's 34.What
made you think it was 19?" I drained my glass. "According to Carl E Linderholms
great classic "Mathematics Made Difficult",the next term is always 19,whatever
the sequence : 1,2,3,4,5 -19 and 1,2,4,8,16,32 - 19.Even 2,3,5,7,11,13,17
- 19."
"That's ridiculous. "No,it's simple and general and universally applicable
and thus superior to any other solution.The Laplace interpolation formula
can fit a polynomial to any sequence whatsoever,so you can choose whichever
number you want to come next,having a perfectly valid reason.For
simplicity,you always choose the same number."
"Why 19?",Dennis asked. "It's supposed to be one more than your favourite
number," I said,"To fool anyone present who likes to psychoanalyse people
based on their favourite number."
"Nonsense,I'll tell you the real answer,"Adam said.
"Each number is the sum of the previous two. So the
next is 13+21,or 34,then 55,then 89,then 144 and so on. It's the -"
"Fibonacci sequence," I interrupted. "God,I'm
so fed up with the blasted Fibonacci sequence! even the name's phoney! Leonardo
Fibonacci,son of Bonacci!" That's a nickname invented by Guillame Libri in
1838,long after Fibonacci died.
The famed Fibonacci was in fact named Leonardo Pisano Bigolo.Pisano means
that he lived in Pisano one knows what Bigollo means. At any rate,his sequence
ought to be called the Leonardo Pisano Bigollo sequence,except that's too
long."
"You mathematicians have a lot of attitude." Dicky remarked. "At least,an
attitude that differs from most other people's."
"Proof," Adam declared."Mathematicians always
want to prove things.That's certainly a strange attitude. Never understood
why myself. If you keep trying it,and it keeps working,it's got to be
right! So why waste time getting into all sorts of logical tangles proving
the silly thing?"
"Well,why don't you physicists bother doing experiments? If a theory
tells you what you want to hear,why not just assume
it's true?" "Because you can't just go around believing theories without
testing them!"
"And mathematicains don't think you can go around believing theorems without
proving them. Alexander why do lawyers insist
on cases being tried in court? Why not just let the judge look at the
evidence and decide whether the defendant has committed the crime?" "You
can't do that! There would be a miscarriage of justice!"
"Right.That's what mathematicians worry about when they insist on proofs.They
don't want to find out later that they were wrong.It might be
embarassing."
Adam shook his head sadly,"You know full well it's not like that.Mathematics
is basically simple.If you can see an obvious pattern
it can't be coincidence.Why bother to prove it?"
I thought for a few sceconds,"I'll give you an example.Here's a sequence,and
I want you to tell me the next number."
"I'll do my best." "1,1,2,3,5,8,13,21,34,55," I said. He looked puzzled.
"Don't be silly.I just asked you that one.It's the Fibonacci sequence."
"Is it? Then what's next?"
"89," Adam replied, "Wrong,it's 91."
"But it looks like the -"
"You're leaping to conclusions,Adam based on previous prejudices.Most
injudicious.Your sequence was the Fibonacci sequence,but the nth in my sequence
is the least integer not less than
Öen-2, where
e=2.71828,the base of the natural logarithms.I want the 11th term,which is
the least integer not less than,or 90.017.That's 91."
"Humph.Well that's an accident,a rare exception.I'll believe you if
you can show me some more examples of misleading sequences."
Alexander interjected,"Can you? Or have you exhausted your repetoire?"
[The matter should not rest by being shown a number of examples -
this is how people come to "believe" things - a weight in it's favour
- mathematicians require something more scrupulous - that whatever has been
shown is incontrovertibly true REGARDLESS of what anyone wishes to believe
- it is not a matter of personal opinion guided by number of examples
- but an in principle matter of reasoning that something MUST be the
case.Such matters are not for anyone to "believe"
- but to accept because they are true - no matter what one would
have believed - The Mutilated Chess Board is
such an example - LB]
"There are hundreds," I said, "It's easier than you think.Richard K.Cuvy,a mathematician at the University of Calgary,collects them.He refers to them as the Strong Law of Small Numbers.There aren't enough smal numbers to meet the many demands placed on them,so what look like patterns involving small numbers might just be coincidence.And often are."
I showed them 11 sequences that looked like the Fibonacci numbers,or the alternate Fibonacci numbers 1,2,5,13 and so on. I asked them to decide which were Fibonacci forgeries.
My companions began to argue about whose solution was
right when I proposed one last puzzle.
"What is the next term in the sequence 3,5,7,11,13,17,19.." - I carried
on for some time,listing the odd primes,"....331,337?"
"Those are odd primes," Adam said,"You can't generate that many primes by
accident.The next term must be 347."
"Are you sure?" I asked quietly.
[A lesson in assuming something by number of examples - a notion that
carries over into other areas of life - just because something has happened
N times - doesn't mean it will happen on the N+1st. One can use probability
theories to discern likelihoods - but even then what ACTUALLY happens may
not be due to the perceived pattern so far. Note that number sequences
are used in intelligence tests and often there is a presumed correct answer
and if you don't get that then you are said to be unintelligent - given that
interpolation techniques can generate any answer from a given sequence -
the intelligence test is really not a matter of
generating THE answer - but generating AN answer that is logically consistent
and follows a reasoned argument - the novelty of the argument is what
shows intelligence - not the generating of a solution provided
by the question setter- LB]
Fibonacci or Forgery?
1.) 2,3,5,8,13......an,where an equals 1 plus the sum of the first n terms of the Fibonacci sequence.eg a1=1+1, a2=1+(1+1)=3, a3=1+(1+1+2)=5 etc.
2.) 1,3,8,21,55....an,where an equals the sum of the first n terms of the sequence formed by removing every other Fibonacci number.So a1=1, a2=1+2=3, a3=1+2+5=8 etc.
3.) 1,1,2,3,5,8...where an is the number of ways in which you can arrange n coins in horizontal rows,such that all the coins in each row touch,and every coin above the bottom row touches two coins in the rows below it.
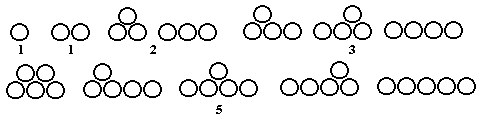
4.) 1,2,5,13...an.Same as 3.) except that now n is the number of coins in the bottom row.
5.) 1,2,5,13...an where an = (n-1)2n-2 +1.
6.) 1,2,5,13...an as defined by the number of disconnected graphs with n+1 vertices.
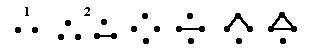
7.) 1,1,2,3,5,8...an where an equals the integer nearest ((1+Ö5)/2)n/Ö5.
8.) 1,2,5,13...an defined by the number of
connected graphs with n+2 vertices having just one cycle.
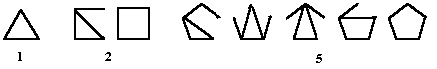
9.) 1,2,5,13...an where an is the coefficient of xn+2/(n+2)! in the power series solution to the differential equation y=exy,which starts y = 1 + x2/2! + x3/3! + 2x4/4! + 5x5/5! + 13x6/6!...
10.) 1,2,5,13...an where an equals an-1 + nan-2 when a-1 = a0 = 1/2.
11.) 2,3,5,8,13...an In this sequence apartment blocks of n floors are to be painted blue and yellow,with the rule that no two adjacent floors can be blue (but they can be yellow).Let an be the number of ways to paint n floors.
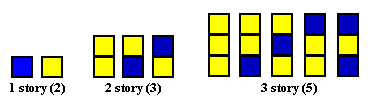
Solutions
1.) Fibonacci.Eg to form a6,you add 8,the sixth term in the Fibonacci sequence. The sum is 8+13,is a sum of consecutive Fibonacci numbers. By definition,then,the answer 21,is itself a Fibonacci number.This patterns continues.
2.) Fibonacci. Eg to go from a5 to a6,you add 89.The sum is 55+89,a sum of consecutive Fibonacci numbers. By definition,then,the answer,144,is itself a Fibonacci number.This pattern continues.
3.) Forgery.The sequence continues 12,18,26.
4.) Fibonacci. The proof depends on the identity f 2n-1 = f 2n-3 + 2f2n-5 + 3f2n-7 +.....+(n-1)f1+1 for Fibonacci numbers fn.
5.) Forgery.The sequence continues 33,81,193.
6.) Forgery. The sequence continues 44,191,1229,13588.
7.) Fibonacci.This pattern follows from Binet's formula fn = [((1+Ö5)/2)n+((1-Ö5)/2)n]/Ö5.
8.) Forgery. The sequence continues 33,89,240,657,1806.
9.) Forgery. The sequence continues 36,109,359,1226.
10.) Forgery. The sequence continues 38,116,382.
11.) Fibonacci. Consider eg. a five-floor building.The fifth floor can be either yellow or blue.If it is yellow,the rest of the building can be painted in any possible way for a four-four building.If it is blue,the fourth floor must be yellow and the rest of the building can be painted in any possible way for a three-floor building.So a5 = a4 + a3,as it is for Fibonacci. The pattern is general.
Odd Prime Sequence: Forgery. The sequence 3,5,7,....331,337 and so on consists of all the numbers n that divide 2n-1-1 exactly. The next term is 341,which is not prime (11 x 31 = 341) but divides 2340-1.
| MP3 759K |
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
SCIENTIFIC AMERICAN File Info: Created 9/3/2002 Updated 25/08/2012 Page Address: http://leebor2.100webspace.net/Zymic/forgeries.html