A theory of everything
 |
Is there a single deep idea that unify the apparent diversity of nature?
Are the beguiling patterns discovered in particle physics clues to a theory
of everything? Some physicists would answer yes to both questions.
Steve Adams
ALBERT EINSTEIN once said: "The most incomprehensible thing about the Universe is that it is comprehensible." The Universe is unbelievably large and contains an unthinkable number of things. Yet we can model much of its history, account for its structure, predict its future and understand the behaviour of a bewildering variety of the objects it contains. We can do this because we understand that everything is bound together by a web of relationships. We call them the laws of physics.
But why these laws, and not others? Einstein dedicated the final decades
of his life to a search for a single unified field theory that would govern
all the laws of physics as we know them. He was unsuccessful in this quest
for a theory of everything (TOE), and by the time
he died in 1955 he had become cut off from the mainstream of physics, which
had by then become preoccupied with the consequences of
quantum theory
and the discovery of new sub atomic
particles and forces. Nearly half a century later, physicists are again
talking about unification. And there are good reasons to believe that they
may succeed where Einstein failed.
Everything is one
The law of laws
THE job of a good physical law or theory is to summarise a range of behaviours in a simple way by pointing out the patterns that are common to all of them. For example, planets, comets, stars and galaxies follow many different trajectories through space, but these can all be derived from Newton's law of gravitation.
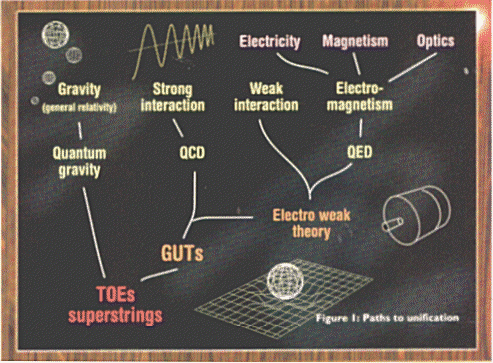
A TOE would do a similar job-except that it would cover not just the motions of astronomical bodies but all the basic properties of the Universe (Figure 1). It would predict what particles can exist, what their properties must be, and how they interact.
This article considers the quest for such a theory over the past two centuries.
By the 1820s it was clear that electric currents create magnetic fields, and in 1821 Michael Faraday devised a simple electric motor that exploited this fact. He, like Einstein, had a deep faith in the unity of nature, and assumed that if electric currents can induce magnetic forces, then magnetic effects should be able to induce electric currents. He discovered this effect, which we call electromagnetic induction, in the 1830s. It is the single most important principle involved in the generation and transmission of electrical energy.
Faraday made one other major discovery related to unification: he showed that magnetic fields can affect light by rotating its plane of polarisation. This discovery convinced him that light must be linked to electricity and magnetism, and confirmed his belief that all the forces of nature spring from a common origin. By the mid-1800s it was clear that electricity, magnetism and optics were linked, and the hunt was on for a unifying theory. The British physicist James Clerk Maxwell provided it. He was intrigued by Faraday's intuitive pictorial approach to electromagnetism and worked out four mathematical equations that lay behind Faraday's pictures of electric and magnetic fields. Maxwell's equations give a complete description of electric and magnetic fields.
But that's not all. The equations imply that a disturbance of the fields will travel outwards as a wave with a velocity equal to about 3 x 108 metres per second, the speed of light. This confirmed Faraday's belief that light itself is an electromagnetic wave and implied that there must be other electromagnetic waves invisible to us, and in 1888 the German physicist Heinrich Hertz demonstrated the generation and detection of radio waves.
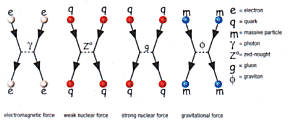 |
| Figure 2: Feynman's interpretation: quantum field theories explain all the forces of nature in a similar way-by an exchange of force-carrying particles |
So by the beginning of the 20th century electricity, magnetism and optics had been put on a unified footing. The only other force law known at the time was the Law of gravitation. Faraday had tried to detect a gravitational influence on light. Though he failed, he remained confident that gravity and electromagnetism must be linked. With Newton's laws of mechanics predicting how masses move under the influence of forces, and electromagnetism and gravitation providing those forces, it looked as though everything might be explained by mechanics and electromagnetism (see Inside Science No.15). But there was trouble ahead.
It was Einstein who realised that mechanics and electromagnetism were incompatible. He asked himself what a light beam would look like if one could move alongside it at the speed of light. Newton's mechanics predicted that it should look like a stationary disturbance of the electric and magnetic fields, but in Maxwell's theory this is impossible. This was disturbing to Einstein. He believed that the laws of physics should be the same for all observers, whatever their state of motion. Maxwell's equations predict that electromagnetic waves travel at a fixed speed of about 3 x 108 metres per second regardless of how fast an observer or the light source moves. Mechanics, however, predicts that the speed of light will change if an observer is moving relative to its source or to the hypothetical medium through which it moves. So there was a contradiction.
In 1905 Einstein took the bold step of asserting that the laws of physics really are the same for all observers moving at a uniform velocity. This is the principle of relativity. It means that the speed of light must be the same for all observers, so however fast you run light always moves away from you at the same speed. This means that the laws of mechanics have to change, as space and time must be different for different observers: moving clocks run slow, moving rods contract, mass increases with velocity, energy has mass and vice versa. Einstein worked out these consequences in great detail and, to the surprise of many of his contemporaries, they were confirmed by experiment (see Inside Science No.49).
Three years later, Einstein's old mathematics teacher, Hermann Minkowski, pointed out that the mathematics of special relativity is similar to the mathematics of rotation. If you rotate a shape on a piece of graph paper the coordinates of its corners all change, but the shape retains properties such as area, angles and lengths of sides. In a similar way, motion changes the space and time coordinates of events, but certain characteristics stay the same-in particular, a property called the "interval" which is like a four-dimensional distance between events.
If the world is regarded as a four- dimensional continuum in which time is treated on more or less the same footing as space, then relativity can be interpreted as a geometric theory. Minkowski called this four-dimensional world space-time. Einstein resisted the idea at first but soon realised its power. Without it he could not have formulated his masterpiece, the general theory of relativity-a geometric theory of gravity (see Inside Science No.31).
Einstein's first great theory is called special relativity because it describes physics from the point of view of a uniformly moving vehicle; the effects of gravitation are not automatically built in. But Einstein wanted a theory that worked for all observers, even if they are accelerating or in a gravitational field. The key to solving this problem came in a flash of inspiration when he realised that a freely falling observer does not experience gravity; this is the situation for astronauts in a space station. On the other hand, someone in an accelerating rocket is pressed against the floor as if they are in a gravitational field. Gravity and acceleration are in a sense equivalent. But how can they he represented in space-time?
The answer is that gravity distorts space-time geometry just as you distort a bed by sitting on it. The general theory of relativity treats gravitational fields as local distortions of space caused by the presence of matter. These distortions affect the trajectory of other particles. This was paraphrased by the American physicist John Wheeler: matter tells space how to curve, space tells matter how to move.
So far, so good. Having created geometrical mechanics and shown that gravity arises as a distortion of space-time geometry, Einstein tried to extend general relativity to include electromagnetism. His holy grail was a unified field theory that would explain mechanics, electromagnetism and gravitation in a single set of equations. He was so confident in this that he ignored the developments in nuclear physics leading to the strong force, responsible for binding protons and neutrons in the nucleus, and the weak force involved in some types of radioactive decay. While many scientists had come to believe that on the microscopic level quantum theory ruled physics, Einstein could not accept this. He felt that quantum theory, based on indeterminism and probability, could not be a true representation of any underlying reality (Figure 6).
In the 1920s and 1930s Einstein tried to join electromagnetism, mechanics and gravitation by adding a fifth dimension to the four of space-time. This had been suggested by a German mathematician, Theodor Kaluza in 1919, and it almost worked. But however much he played with the equations they never came out quite right. The only way that the fifth dimension could be made to behave was if it was curled up in a loop so small that it would have no observable consequences.
The killer blow, however, came from the unquestionable successes of quantum theory (see Inside Science No.25). Quantum theory's discontinuous jumps and probabilistic processes are at odds with the continuity of classical field theories, including general relativity. It seemed that the key to the Universe would turn out to be some thing quite different from Einstein's vision.
Quantum field ideas
Swapping particles
IN the 1930s the big question was how to write down the quantum mechanical equations describing the interaction of light and matter. The physicists Richard Feynman and Julian Schwinger from the US and Shin'ichiro Tomonaga from Japan solved the problem with quantum electrodynamics (QED) in the 1940s. In QED, the forces between charged particles arise from a continual exchange of other force- carrying particles, in this case photons. In this picture, electrons repel one another and attract protons by an exchange of photons (Figure 2). It is analogous to the way two people who play "catch" with a heavy ball are pushed apart, but QED explains attraction too. Physicists used QED to calculate the electron's magnetic moment- effectively its intrinsic magnetism-to 10 significant figures, and their results agreed with experimental measurements.
The amazing success of QED inspired theorists to try to construct similar exchange theories for the newly discovered strong and weak nuclear forces (see Inside Science No. 17). Abdus Salam, Steven Weinberg and Sheldon Glashow showed
that the mathematics could be extended to explain the weak interaction-but for this, three new force-carrying particles were required. This trio, the W+, W- and Z0 particles, were duly discovered at CERN, the European Laboratory for Particle Physics near Geneva, in the mid-1980s (see Inside Science No.63).
This electroweak theory, uniting electromagnetism and the weak force, picked up where Maxwell had left off. It then seemed logical to suppose that the strong force would soon be incorporated too, and to some extent this has been done. Discoveries in particle physics implied that the strong force comes from a more fundamental interaction between the quarks that make up all strongly interacting particles. This is the colour force. Quantum chromodynamics (QCD) accounts for the colour force by introducing a new set of force-carrying particles, the gluons, that are exchanged by quarks. Unfortunately calculations in QED are incredibly difficult and cannot be carried out to any thing like the precision of corresponding calculations in QED.
Nonetheless, physicists believe it may be possible to "bolt on" QED to electroweak theory to create a grand unified theory (GUT) of all particle interactions. QED, electroweak theory and QCD form a mathematical hierarchy based on the notion of symmetry (see Box). Two Americans, Chen Ning Yang and Bob Mills, developed the links which are now known as Yang-Mills theories.
If these ideas work out, physicists will have shown that electro magnetism, the weak force and the colour force all derive from a single superforce. The strengths of the three interactions are very different under normal experimental conditions, but at the high temperature and pressure that existed immediately after the big bang they would have been similar.
For the past century, a succession of new and ever more exotic particles has been predicted and discovered in a wide variety of detectors around the world. The neat picture of atoms made of protons, neutrons and electrons has given way to a menagerie of particles: hadrons (such as protons and neutrons), electron-like particles or "leptons", and force carriers (such as photons and gluons).
In the 1960s, physicists realised that the hadrons could be arranged according to their properties to form simple geometric patterns. The most famous of these hadronic patterns is called the eightfold way and was discovered by the American physicist Murray Gell Mann and his Israeli colleague Yuval Ne'eman in 1960. Just as the periodic table of the elements can be explained in terms of an underlying atomic structure, the hadron patterns were explained in terms of more fundamental particles which became known as quarks (the terms "ace" and "patton" were also used for a while). In the picture known as the Standard Model, three different "generations" of quarks and leptons are required. Each quark or lepton generation contains a pair of particles, making six quarks and six leptons in all (see tables in Inside Science No.63). The Standard Model also requires 12 force- carrying particles.
Beyond the standard
Fruits of symmetry
ONE troubling aspect of the Standard Model is that it includes about 20 parameters that have to be "accommodated" or adjusted to fit the experimental data, rather than derived from first principles. These include even such basic quantities as the mass of an electron. This arbitrariness is deeply unsatisfying to physicists. So they are on the look out for a more universal theory from which these fundamental values can be derived in the same way that Maxwell's equations gave a value for the speed of light. The symmetry embodied in the Yang Mills quantum field theories is the main clue theoretical physicists have in their hunt for a GUT. The higher the order of symmetry, the more particles there are: one photon, four electroweak force carriers, eight gluons and so on. Beyond this, at even higher orders of symmetry, new and as yet undiscovered particles are predicted.
To be successful, a GUT must have a symmetry of high enough order to include the symmetries of the component theories. It must also somehow account for the as yet unexplained symmetry between quarks and leptons, with each having three generations apparently mirroring one another. The as yet undiscovered particles predicted by the high-order symmetries will provide a way to test the theory. If such particles can be found experimentally, it will be evidence that the theory is valid.
One leading approach, called super-symmetry (SUSY), predicts the existence of a new supersymmetric particle for every known particle. But none of these super-symmetric particles, or sparticles, has yet been detected. Other proposed GUTs that link leptons and quarks include interactions that can interconvert the two kinds of particle. A consequence of such a theory would be that protons could decay when quarks within them turn to leptons. This would mean that all matter as we know it is ultimately unstable. Attempts to detect the decay of protons have so far failed, showing that if protons decay at all they must have a half-life of at least 1032 years.
 |
TO unify our experiences we need to recognise
similar patterns in different events and processes. It's something that most
of us are usually good at, and it is closely linked to ideas of symmetry.
In fact, we often regard symmetrical patterns as particularly beautiful and
incorporate them into music, art and architecture. Recognising symmetry
simplifies things, so that by knowing part of a pattern we can predict much
of the rest of it and find clues to underlying relationships. A good physical
theory should summarise a wide range of behaviour in a very simple way by
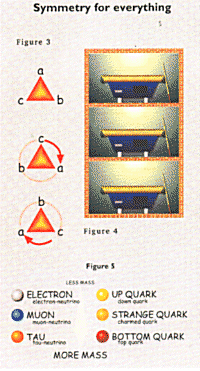
pointing out common patterns. With rotational symmetry, a structure will look the same when rotated through a range of angles. For example, it is what happens with an equilateral triangle (Figure 3) when rotated through any multiple of 600. A typical example of physical symmetry is shown by billiard balls (Figure 4) which will always behave in the same way on a similar table regardless of whatever floor of a building the table is on. This implies that the position in the gravitational field is irrelevant-moving up a floor is like rotating the triangle above. Thus it is OK to measure gravitational energies of billiard balls from any convenient level. Unexpected patterns among otherwise distinct particles hint at an underlying symmetry leading to new physical laws. This is the case with leptons and quarks (Figure 5). When the muon (a kind of heavy electron) was first discovered, it was a complete surprise. However, we now know that it is one of three generations of related particles, each of which has its own neutrino. More over, quarks also form three generations with a pair of particles in each. A TOE must be able explain this symmetry. |
The failure to detect the characteristic particles and interactions of SUSY and other proposed GUTs is not the only source of doubt about these theories. When they are used to calculate the out comes of particular events, the usual approach is to consider all possible ways in which the event can take place and then add the contributions one by one. But this often leads to seemingly impossible results, such as an infinite value for the energy of empty space. And there is still the difficulty of gravity. GUTs only deal with known particle interactions. They do not even attempt to embrace gravity as well.
How can Einstein's theory of general relativity, with its continuous space-time geometry, be combined with discontinuous quantum field theories? There is one approach that claims to solve these problems. It is called superstring theory.
The Standard Model treats leptons,quarks and force-carrying bosons as different point-like fundamental particles. In string theory, by contrast, they all derive from the same fundamental structure-an extended string. In this picture, the differences we see between, say, electrons and neutrinos or up and down quarks are due to different ways in which the strings can vibrate-just as the different harmonics present in the sounds emitted by a guitar string arise from different standing waves on the string. There are an infinite number of possible modes of vibration so there are, in principle, an infinite number of possible particles. Only a handful are observed because the rest involve very high energies.
We can draw another analogy with the guitar string. Just as musical harmonics form a regular mathematical pattern, with the frequencies increasing in a regular way, so particles also form patterns, albeit rather more complicated ones. The pattern of harmonics derives from the one-dimensional nature of the string and its fixed ends. In string theory, the complex symmetries between particles and their interactions require more dimensions, and in this respect string theory harks back to Kaluza's ideas. If the Universe has 10 dimensions, rather than the four of space-time or the five derived from Kaluza's old theory, then the symmetries of all the Yang-Mills field theories can be incorporated in a single self-consistent GUT And it does not stop there. One of the features of string theory is that it actually predicts the equations of general relativity.
Another hopeful sign is that at low energies, string theory behaves like the supersymmetry of previous GUTs (hence the name superstring), and so predicts the existence of sparticles. This is important because most of the predictions of string theory involve energies so high that it is unlikely we shall ever be in a position to test them. However, sparticles are predicted to have masses around 100 to 1000 times that of a proton. This means we should be able to detect them in present accelerators or their successors, such as the Large Hadron Collider that should come into operation at CERN around 2005.
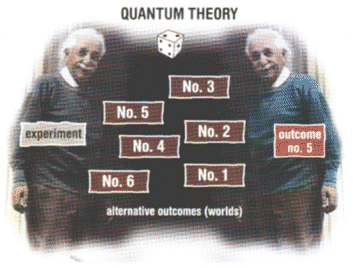 |
| Figure 6: In quantum theory the same experimental conditions can lead to different final outcomes. The theory predicts the probability of each outcome but doesn't say which will actually occur. Einstein objected to this, saying "God does not play dice". But experimental results support quantum theory |
A leap of faith?
Untestable theories
IF superstring theory is correct, it raises awkward questions about the nature of physics. Six of the 10 dimensions of the Universe inhabited by strings are curled up in little circles (the technical term is compactified), not much larger than the Planck length, which is 1020 times smaller than the diameter of a nucleus. This is why we see just three spatial dimensions and one of time. But this poses a problem for experimental physics. We can never expect to carry out experiments to probe these compactified dimensions, because doing so would involve unimaginably high energies.
So why is such an exotic and mainly untestable theory making such an impact in theoretical physics? It is the only theory that avoids all the infinities of GUTs. It is the only theory that constrains the number of dimensions (it only works in 10 or 26 dimensions). It is the only theory in which gravity is not left out in the cold. And it is the only theory that can cope with the effects of quantum theory on space-time, which requires that on the smallest scale the geometry of space-time must be intrinsically uncertain-a prediction at odds with the smooth, continuous nature of general relativity. Perhaps most appealing, superstring theory is full of deep symmetries capable of generating all the patterns and relationships we see in particle physics and on which the macroscopic world depends. The downside is that the mathematics is formidable, and no one has managed yet to use the theory to derive any fundamental property, such as the mass of the electron, from first principles.
We are approaching a period when the most powerful theory in physics may have to be taken on the merit of its internal beauty and consistency, rather than its detailed correspondence with experiment. Of course, this is nothing new. It was a faith in the internal symmetries and simplicity of nature that inspired Faraday, Einstein, Feynman and others on the path toward unification in the first place.
If today's high hopes are realised, and string theory or a competing theory, emerges as the real TOE what then? Will it gives us the means to predict anything and everything, from particle interactions to the evolution of the Universe? Probably it will help us with both these extremes of the physical Universe, because they depend in large part on the interplay between the fundamental forces. But it will be of little help in the middle ground, such as chemistry and biology. It is here that we find the things that have the most direct hearing on our daily lives.
© Reed Business Information 1999. Educational copying
of Inside Science is permitted under licence of Copyright Licensing Agency
Limited, 33 - 34 Alfred Place, London WC1 7DP
Back numbers of Inside Science are available
from New Scientist, P.O. Box 666, London ElS 1DW. Inquiries 0181
5030589.