The Mathematical Experience

by Philip J Davis & Reuben Hersh

8.Four Dimensional Intuition (p400)

A LINE IS one-dimensional. A flat surface is two- dimensional. Solid objects are three-dimensional. But what is the fourth dimension?

Sometimes people say that time is a fourth dimension. In the physics of Einstein's relativity, a four-dimensional geometry is used in which a three-dimensional space and a one-dimensional time coordinate are merged into a single four-dimensional continuum. But we don't want to talk about relativity and space-time. We only want to know if it makes sense to take one more step in the list of geometrical dimensions.

For instance, in two dimensions, we have the familiar figures of the circle and the square. Their three-dimensional analogs are the sphere and the cube. Can we talk about a four-dimensional hypersphere or hypercube, and make sense?

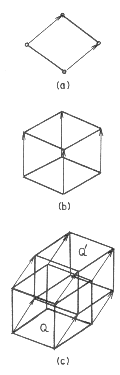
We can go from a single point up to a cube in three steps. In the first step, we take two points, 1 inch apart, and join them. We get a line interval, a one-dimensional figure. Next, we take two 1-inch line intervals, parallel to each other, 1 inch apart. Connect each pair of end-points, and we get a 1-inch square, a two-dimensional figure. Next. take two 1-inch squares, parallel to each other. Say the first square is directly above the second, 1 inch away. Connect corresponding corners, and we get a 1-inch cube.

So, to get a 1-inch hypercube, we must take two 1-inch cubes, parallel to each other, 1 inch apart, and connect vertices. In this way, we should get a 1-inch hypercube, a figure dimensional figure.

The trouble is that we have to move in a new direction at each stage. The new direction has to he perpendicular to all the old directions. After we have moved back and forth. then right and left, and finally up and down, we have used up all the directions we have accessible to us. We are three- dimensional creatures, unable to escape from three-dimensional space into the fourth dimension. In fact, the idea of a fourth physical dimension may be a mere fantasy, a device for science fiction. The only argument for it is that we can conceive it; there is nothing illogical or inconsistent about our conception.

We can figure out many of the properties that a four-dimensional hypercube would have, if one existed. We can count the number of edges, vertices, and faces it would have. Since it would be constructed by joining two cubes, each of which has 8 vertices, the hypercube must have 16 vertices. It will have all the edges the two cubes have; it will also have new edges, one for each pair of vertices that have to be connected. This gives 12 + 12 + 8 = 32 edges. With a little more work, one can see that it will have 24 square faces, and 8 cubical hyperfaces.

The table below shows the number of "parts" of the interval, square, cube, and hypercube. It is a startling discovery that the sum of the parts is always a power of three!

Dimension	OBJECT	0-Faces (Vertices)	1-Faces (Edges)	2-Faces (Faces)	3-Faces	4-Faces
0	Point	1
1	Interval	2	1
2	Square	4	4	1
3	Cube	8	12	6	1
4	Hypercube	16	32	24	8	1

In a course on problem-solving for high-school teachers and education students, the gradual discovery of these facts about hypercubes takes a week or two. The fact that we can find out this much definite information about the hypercube seems to mean that it must exist in some sense.

Of course, the hypercube is just a fiction in the sense of physical existence. When we ask how many vertices a hypercube has, we are asking, how many could it have, if there were such a thing. It's like the punch line of the old joke- "If you had a brother, would he like herring?" The difference is that the question about a nonexistent brother is a foolish question; the question about the vertices of a non- existent cube is not so foolish, since it does have a definite answer.

In fact, by using algebraic methods, defining a hypercube by means of coordinates, we can answer (at least in principle) any question about the hypercube. At least, we can reduce it to algebra,just as ordinary analytic geometry reduces questions about two- or three-dimensional figures to algebra. Then, since algebra in four variables is not essentially more difficult than in two or three, we can answer questions about hypercubes as easily as questions about squares or cubes. In this way, the hypercube serves as a good example of what we mean by mathematical existence. It is a fictitious or imaginary object, but there is no doubt about how many vertices, edges, faces, and hyperfaces it has! (or would have, if one prefers the conditional mode of speaking about it.)

The objects of ordinary three- or two-dimensional geometry are also mathematical objects, which is to say, imaginary or fictitious; yet they are closer to physical reality, unlike the hypercube which we cannot construct.

The mathematical three-cube is an ideal object [This is why they are not "ghosts" as R.Pirsig say in "Zen and the Art of Motorcycle Maintenance" -LB] , but we can look at a wooden cube and use it to determine properties of the three-cube. The number of edges of the three- cube is 12; so is the number of edges of a sugar cube 12. We can get a lot of information about two- and three-dimensional geometry by drawing pictures or building models and then inspecting our pictures or models. While it is possible to go wrong by misusing a picture or model, it is rather difficult to do so. It takes ingenuity to invent a situation where one could go wrong in this way. As a general rule, the use of pictures and models is helpful, even essential in understanding two- or three-dimensional geometry.

Reasoning based on models and figures, either actual ones or mental images of them, would be called intuitive reasoning, as opposed to formal or rigorous reasoning.
When it comes to four-dimensional geometry, it might seem that since we ourselves are mere three-dimensional creatures, we are excluded by nature from the possibility of reasoning intuitively about four-dimensional objects. And yet, it is not so. Intuitive grasp of four-dimensional figures is not impossible.

At Brown University Thomas Banchoff, a mathematician, and Charles Strauss, a computer scientist, have made computer-generated motion pictures of a hypercube moving in and out of our three-dimensional space.[The same thing has ben done with 4D Julia sets -LB] To understand what they have done, imagine a flat, two-dimensional creature who lived at the surface of a pond and could see only other objects on the surface (not above or below). This flat fellow would be limited to two physical dimensions, just as we are limited to three. He could become aware of three dimensional objects only by way of their two-dimensional intersections with his flat world.

If a solid cube passes from the air into the water, he sees the cross sections that the cube makes with the surface as it enters the surface, passes through it, and finally leaves it.
If the cube passed through repeatedly, at many different angles and directions, he would eventually have enough information about the cube to "understand" it even if he couldn't escape from his two-dimensional world.[In other words,your eyes aren't good enough -LB]

The Strauss-Banchoff movies show what we would see if a hypercube passed through our three-space, at one angle or another. We would see various more or less complex configurations of vertices and edges. It is one thing to describe what we would see by a mathematical formula. It is quite another to see a picture of it; and still better to see it in motion. When I saw the film presented by Banchoff and Strauss, I was impressed by their achievement,* and by the sheer visual pleasure of watching it. But I felt a bit disappointed; I didn't gain any intuitive feeling for the hypercube.
[ * This film, incidentally, won Le Prix de la Recherche Fondamentale au Festival de Bruxelles, 1979. ]

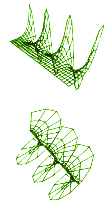The complex exponential function (a four-dimensional object) looked at from several points of view. Courtesy:Banchoff  & Strauss productions

A few days later, at the Brown University Computing Center, Strauss gave me a demonstration of the interactive graphic system which made it possible to produce such a film. The user sits at a control panel in front of a TV screen. Three knobs permit him to rotate a four dimensional figure on any pair of axes in four-space. As he does so, he sees on the screen the different three-dimensional figures which would meet our three-dimensional space as the four-dimensional figure rotates through it.

Another manual control permits one to take this three- dimensional slice and to turn it around at will in three- space. Still another button permits one to enlarge or shrink the image; the effect is that the viewer seems to be flying away from the image, or else flying toward and actually into the image on the screen. (Some of the effects in Star Wars of flying through the battle-star were created in just this way, by computer graphics.)

At the computing center, Strauss showed me how all these controls could be used to get various views of three-dimensional projections of a hypercube. I watched, and tried my best to grasp what I was looking at. Then he stood up, and offered me the chair at the control.
I tried turning the hypercube around, moving it away, bringing it up close, turning it around another way. Suddenly I could feel it! The hypercube had leaped into palpable reality, as I learned how to manipulate it, feeling in my fingertips the power to change what I saw and change it back again. The active control at the computer console created a union of kinesthetics and visual thinking which brought the hypercube up to the level of intuitive understanding.

In this example, we can start with abstract or algebraic understanding alone. This can be used to design a computer system which can simulate for the hypercube the kinds of experiences of handling, moving and seeing real cubes that give us our three-dimensional intuition. So four- dimensional intuition is available, for those who want it or need it.

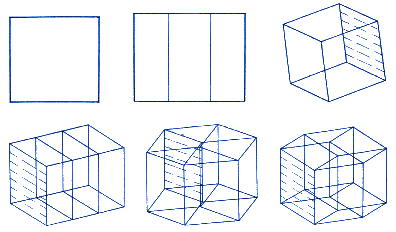Six views of a hypercube extracted from a general computer graphics system for the real time display of four dimensional "wire frame" objects. Courtesy: Banchoff and Strauss Productions.

The existence of this possibility opens up new prospects for research on mathematical intuition. Instead of working with children or with ethnographic or historical material, as we must do to study the genesis of elementary geometric intuition (the school of Piaget), one could work with adults, either trained mathematically or naive, and attempt to document by objective psychological tests the development of four-dimensional intuition, possibly sorting out the roles played by the visual (passive observation) and the kinesthetic (active manipulation.) With such study, our understanding of mathematical intuition should increase. There would be less of an excuse to use intuition as a catchall term to explain anything mysterious or problematical.

Looking back at the epistemological question, one wonders whether there really ever was a difference in principle between four-dimensional and three-dimensional. We can develop the intuition to go with the four-dimensional imaginary object. Once that is done, it does not seem that much more imaginary than "real" things like plane curves and surfaces in space. These are all ideal objects which we are able to grasp both visually (intuitively) and logically.

Further Readings. See Bibliography H. Freudenthal [1978]; J. Piaget, [1970, 71]; T. Banchoff and C. M. Strauss