

Fractals obtained from repeated reflections in circular mirrors produce
breathtaking kaleidoscopic images. Understanding these pictures may give
us new insights into the geometry of chaos
Caroline Series
Most people have become familiar in recent years with pictures
of fractals - those elusive shapes that, no matter how you magnify them,
still look infinitely crinkled. The pictures you saw were probably drawn
by computer, but examples abound in nature - the edge of a leaf, the outline
of a tree, or the course of a river. Fractal curves differ from those studied
in normal geometry. The curve of a circle, for instance, if magnified
sufficiently, just about - becomes a straight line. A fractal curve, on the
other hand, when viewed on many different scales, from
macroscopic to microscopic, reveals
the same intricate pattern of convolutions. How do you construct a fractal
curve? A simple example is the famous Koch snowflake, invented by Helge von
Koch in 1904. It is an example of a "nowhere smooth" curve.
To draw the snowflake, start with the triangle shown in Figure
la. Then replace each of the sides of this triangle by a bent line as shown
in Figure 1b. At the next stage, Figure 1c, each of these sides in turn is
replaced by the same pattern but on a smaller scale, and so on, ad infinitum,
to obtain finally the snowflake shown in Figure 1d.
|
| Figure 1 The Koch snowflake is a fractal evolving from a simple triangle. |
In recent years, there has been a revolution of interest in
fractals. Previously, only a few people had appreciated the significance
and beauty of these strange shapes. Benoit Mandelbrot (see
Mandelbrot's article last week) drew much attention
to their potential use in describing the natural world. At the same time,
the development of high speed computing and computer graphics has made them
easily accessible and this has drawn many people to study them more closely.
|
| Figure 2 Reflections on a complex plane produce what are called limit sets. Here is a stunning example. |
Another reason for the interest in fractals is that they are
connected with chaos. In mathematics,chaos has a specialised meaning (see
the previous articles in this series). The easiest way to understand chaos
is by some examples.
Suppose a particle is moving in a confined region of space according to a
definite deterministic law. Following the path traced out by the particle,
we are likely to observe that it settles down to one of three possible behaviours
-the geometrical description of which is called an
attractor. The particle may be
attracted to a final resting position (like, for example, the bob on pendulum
as it gradually settles down to rest). In this case, the attractor is just
a point -the final resting position of the bob. Or the particle may settle
down in a periodic cycle (like the
planets in their orbits around the Sun). Here
the attractor is an ellipse and the future motion can be predicted with
astonishingly high accuracy as far ahead as we want. The last possibility
is that the particle may continue to move wildly and erratically while,
nevertheless, remaining in some bounded region of space. The motion of some
of the asteroids, for example, appears to exhibit exactly this phenomenon.
Tiny inaccuracies in measuring the position and speed of the asteroid quickly
lead to enormous errors in predicting its future path. This phenomenon is
the signal of chaotic motion. The regions of space traced out by such motions
are called strange attractors.
Once a particle is attracted to a strange attractor there is
no escaping. Almost anywhere you start inside the attractor, the point moves,
on the average, in the same way, just as no matter how you start off a pendulum,
it always eventually comes to rest at the same point. Although the motion
is specified by precise laws, for all practical purposes, the particle
behaves as if it were moving randomly. The interesting point here is
that strange attractors are very frequently fractals.
You might think that to generate such complicated behaviour,
the equations governing the motion would have to be very complicated. An
important insight of recent years has been that, on the contrary, chaotic
motion frequently follows simple deterministic laws.
Mathematicians like to study idealisations of this kind of phenomenon. They
have found a fertile ground of investigation in what is called the iteration
of polynomials. Polynomials are equations containing one or more variables
raised to some power, such as w = z2 + 1 . Iteration is a process
whereby you take an equation, feed in a particular value for the variable,
z , calculate the answer, w which then becomes the new value of z.
1:Practical uses for imaginary numbers COMPLEX numbers are numbers of the form z = x + Ö-1y. The number y is called the imaginary part of z. No ordinary number can be the square root of -1, because the square of any ordinary number is always greater than zero. Complex numbers can be added, subtracted and multiplied in the ordinary way; provided only that we remember to substitute -1 for Ö-12 whenever it occurs. The complex number x + Ö-1y is frequently represented as the point in the plane with coordinates x,y. This is the representation used in drawing pictures of the Julia set. Complex analysis, the calculus of functions of a complex variable, is used daily in the design of aeroplane wings and electronic circuits, in complicated statistical analyses, in quantum theory and in the making and breaking of top secret military codes. |
The operation is repeated over and over again. Iteration models
deterministic behaviour- each new position of a moving particle, as represented
by the point z, depends on its previous position. In the simplest example
of iterating polynomials, you take a point z and let it evolve over a series
of steps so that the new value of z is the square of the previous value of
z plus a constant. This is expressed as z
Þ z2
+ c where c is a constant. If z and c are complex numbers, we obtain some
interesting results. A complex number contains two variables x and y, where
y is multiplied by an imaginary
number, the square root of minus one (see Box 1). So z is written
as x + Ö-ly. The
plane defined by the coordinates x and y , in which z moves over time, is
called the complex number plane.
Computer modelling can be used to follow the movement of z.
This generates pictures of intricate complexity like those shown in Figures
2 and 3. These are the strange attractors for this model. They are called
Julia sets, after the French mathematician
Gaston Julia who, together with his
contemporary Pierre Fatou, first studied them in 1918. Despite many beautiful
and striking results, this work remained relatively unknown until mathematicians
could draw pictures of Julia sets on a computer.
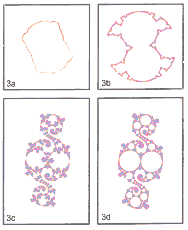 |
| Figures 3a to 3d show further examples of the remarkable patterns produced by non-Euclidean limit sets. |
Towards the end of the 19th century, the German
mathematician Felix Klein
had already studied another kind of set that also merits the name of strange
attractor. Klein was investigating non-Euclidean
geometry, which had been discovered about 50 years earlier. Klein's fractals
arose from iterating not one but several motions of the particle in the complex
number plane. These motions were all of a special kind called inversions,
which are a sort of reflection. The collection of all permitted inversions,
together with those produced by iterating the equations, form what mathematicians
call a group. The particular groups that Klein studied are called, despite
Klein's strong objections, Kleinian groups. In this case, the strange attractor
generated is called a
limit set. Start at any
point you like in the plane and look at the collection of all its images
or "iterates" under all members of the group. These iterates will
always appear to pile up in a certain region of the plane, and this region
is the limit set.
Figures 2,3a,b,c, and d illustrate some of the beautiful examples
of the limit sets obtained in this way. Figure 2 was drawn by the physicist
Roman Tomaschitz, from the University of Brussels, who is interested in these
limit sets because they are related to a possible model for what is
called quantum chaos.
Figures 3a to d were drawn at Harvard University by Curt McMullen, David
Mumford and David Wright.
2: Reflections of a globe on a flat map
|
FIGURE 5 How to project a beachball onto a flat surface. |
FIGURE 5 will remind you of how stereographic projection works.
Think of the globe as a sphere E with the north pole N at the top.
The sphere rests on a horizontal plane
p , touching
p at the south pole
S. Stereographic projection transfers figures on the globe onto figures on
the plane below. To find the image of a point P' on E, join P'
to N by a line. Extend this line beyond P' to where it cuts
p in Q. The point Q
is the protection of P'.
Now reflect E in the equatorial plane l, and try to transfer
the result to the plane
p . The southern hemisphere
projects onto the inside of the circle, centred on S, marked k in Figure
5. As a result of reflection in 1, points inside k are transformed
into points outside k and vice-versa, while points on k remain fixed.
The diagrams opposite illustrate what happens to a point Q inside k under
this transformation. Let P be the point corresponding to Q on E, and
let P' be the image of P under reflection in l. Let Q' = T(P') be
the image of P' under stereographic protection T. In the figure on the far
right, you see the circles T(l) = k and T(c) on
p . These are the images
on p of l and
of the circle c through P and P' which is perpendicular to l.
Both 1 and c, being circles on the horizontal plane
p , project to circles
on p , and furthermore,
since l and c cut at right angles, so do T(l) and T(c). Using
some ordinary geometry about circles which cut at right angles, we get the
formula SQ.SQ'=r2 , where r is the radius of T(l). This
is the general formula for inversion in a circle of radius r.
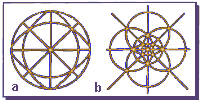
In order to understand inversion, think for a moment about
reflecting in great circles on a sphere. Such reflections produce the beach
ball patterns shown in Figure 4a. Figure 4b shows the beach ball pattern
projected onto a flat surface. Inversion is nothing other than the effect,
as seen on the plane, of reflection in great circles on the sphere. Box 2
explains it in more detail.
Inversion shares with reflection the property that there is
always a "mirror". Instead of being a straight line as in the case of an
ordinary reflection, the "mirror" used for inversions are circles. Inversion
interchanges all the points on one side (inside) of this circular mirror
with all the points on the other side (outside). Points on the circle itself
are left fixed. You can think of ordinary reflection as a special kind of
inversion, in which the circular mirrors have infinite radius.The possibilities
you can get from successive inversions in two circles are rather limited.
In these cases, the limit set - the region where all the images of any particular
point eventually bunch up - consists of either one or two points.
Things begin to get interesting when you start to invert in
three or more circles. Figure 6 is an example of this. We start with a base
circle and draw four other circles. Each of these circles cuts the base circle
at right angles and each touches its two neighbours at the points where they
meet the base circle. We then pick any one of these four circles as the "mirror"
for an inversion. The result is that the three other circles invert into
three touching circles inside the chosen circle. This is because all four
circles meet the base circle at right angles, and because inversion has the
property that it transforms circles into circles and leaves the angle of
intersection between two circles unchanged.
We do the same thing for the other three circles. At the next stage, we invert in each of these 12 new smaller circles in turn, producing in each one a chain of 11 yet smaller touching circles. And so we continue. It is rather like the chain of reflections you see when the hairdresser holds up a mirror behind you so that you can inspect her or his work. The picture called "Les parapluies de Verone" has been obtained in a similar way, but now there are seven initial circles which intersect near the centre of the picture forming the edge of the central blue umbrella.
 |
| Reflecting in great circles on a sphere as in Figure 4a. onto a flat surface produces the inversion shown in Figure 4b. |
Where are the fractals that Klein was studying? So far, fractal
curves do not seem to have entered the scene. In fact, the diagrams we have
looked at so far are analogous to the iteration of our example z
Þz2
+ c when c = 0. In this case, the strange attractor, or Julia set, is nothing
other than the circle of unit radius in the plane.
The reason for this is as follows. When c=0, the sequence of
iterates of a point z is nothing other than the sequence of powers z,
z2, z4, z8 and so on. If a point starts
inside the circle of radius one, after a few iterations, these powers rapidly
approach zero. On the other hand, if we start with a point outside this circle,
the higher powers of z rapidly get larger and the point goes off to infinity.
It is only when we start with a point on the unit circle that its iterates
remain always at a distance one from the origin, moving round and round the
circle forever.
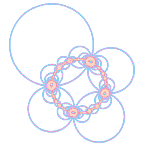 |
| Figure 6 shows how inverting circles produces a chain of reflections. |
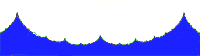
The amazing fact is that we have only to introduce the smallest
possible non-zero value of c and the Julia set gets distorted, not into a
smooth curve roughly circular in shape, but into a fractal like that shown
in Figure 7a.
We can introduce a similar kind of distortion into our inversion example
in Figure 6 by altering the position of the initial circles slightly in such
a way that they no longer cut the fundamental circle at right angles. The
result is that the fundamental circle becomes distorted into a curve that
is a fractal. If we do this in the example of four touching circles, the
overall arrangement of small reflected circles remains the same, but the
circle no longer passes through their meeting points. Instead, at each level,
the small circles form a kind of pearl necklace in which the pearls, instead
of lying smoothly alongside each other in a round chain, get more and more
jostled out of their original positions. Eventually, the individual beads
disappear completely and we are left with the limit set of the distorted
group. It is this process that is illustrated in Figure 3. The picture shown
in Figure 2 is a slightly different example in which some of the initial
circles intersect.
What happens as we gradually distort further and further away
from the initial configuration? Some examples of Julia sets obtained in this
way are shown in Figures 7b and 7c. As we distort in the inversion pictures,
we begin to get the beautiful Paisley patterns appearing in Figure 3.
 |
| Figure 7 shows what happens when we gradually distort the Julia set from a circle. The initial fractal curve in a becomes the "Douady rabbit" in b, and then splits into "islands" in c. |
What happens as we go on distorting? Where does the realm of
distortion end? Sooner or later, it seems, the complication of the curves
must become so great that things break down in some way. This is so, and
what happens in the two cases is not quite the same.
In the case of z Þ
z2 + c , the first thing that happens is that certain
points of the Julia set come together. This is what happened in Figure 7b,
which is often known as a Douady rabbit, after the French mathematician Adrien
Douady whose work includes some of the most important results in this field.
Some time later the poor rabbit's head, ears, nose, legs and tail are all
split off from her body to give the picture in Figure 7c. The Julia set has
broken apart into a lot of "islands". These islands still retain the fractal
property: if you look closely, each island is in fact broken up into many
smaller islands, and so on ad infinitum. In fact, there is no piece of dry
land with any spatial extension at all. A set of this kind is called
a
Cantor set.
We know that strange attractors often take this form.
For inversion groups, the situation is rather different. Total
breakdown happens as soon as any points on the "circular" limit set come
together. Last year, Curt McMullen proved that the points where breakdown
occurs in this way are spread thickly on the boundary of the distortion region
in a manner analogous to that in which recurring decimals are spread thickly
among all numbers. Exactly what happens at the remaining points remains a
mystery . Beyond this point, things get so bad that the whole plane is filled
in by the limit set, so that no interesting pictures can be drawn at
all.
 |
| The picture "Les parapluies de Verone" results from inverting several circles to produce a chain of smaller circles. |
Can we describe those parameter values at which the breakdown
occurs? By parameter values, we mean the c values, or, in the inversion case,
the numbers that describe the initial configuration of circles. It turns
out that in the case of four initial circles, we can describe the initial
configuration entirely by means of one complex number. Once again, we are
in for a surprise. We might legitimately expect the boundary of "nice" parameter
values to be described by a "reasonable" curve. But not so. Let us look at
the situation for z Þ
z2 + c. What we get is the famous
Mandelbrot set
illustrated in many places.
The Mandelbrot set is a plot of the
set of c values at which the Julia set breaks up into islands to form
a Cantor set. It is very important to understand that the Mandelbrot set
is not the Julia set of any particular iteration procedure, but the set of
points in parameter space where a certain type of behaviour breaks down.
The Mandelbrot
set has an amazingly intricate structure. The more you magnify the Mandelbrot
set near a particular c value the more you see what looks like the Julia
set for that same value of c. Extending out of the main body of the Mandelbrot
set are a multitude of hairs.
Along each of these hairs, arranged, in the words of Douady,
"like an infinity of droplets on a spider's web in the morning dew", are
tiny copies of the Mandelbrot set itself. What is the analogy of the Mandelbrot
set for Kleinian groups? Such a set is called a Teichmüller space. Although
mathematicians know a lot about Teichmüller spaces, their actual shapes
have not been much studied. A computer-drawn picture for a case similar to
the inversion example I have described is shown in Figure 8. This picture
was drawn by David Wright. Although it is not so complicated as the Mandelbrot
set, there are still many unanswered questions about its shape. Careful study
is leading to new insights about the way in which the limit-set pictures
vary as they are distorted.
 |
| Figure 8 The limit set of a Teichmüller space which is the equivalent of a Mandelbrot set for Kleinian groups. |
Mathematicians will often tell you that they work on their subject
because it is beautiful. It is sometimes frustrating not to be able to explain
what this means. Over the past few years, computer graphics have come to
our aid. The kind of pictures I have been discussing are surely beautiful
by any standard - there is debate as to whether they should be counted as
a new art form. The mathematical ideas and relations that govern the pictures,
telling us what to draw and what features to study are, to the mathematician,
every bit as beautiful as the pictures themselves. Understanding the pictures
may well give us new insights into the geometry and mechanisms of chaos:
experience shows that the mathematical beauty of today usually translates
into the useful tools of tomorrow.
Caroline Series is a reader in mathematics at the University of Warwick.
| Chaos | Quantum | Logic | Cosmos | Conscious | Belief | Elect. | Art | Chem. | Maths |
New Scientist
Sep1990 File Info: Created Updated
21/3/2016 Page Address:
http://leebor2.100webspace.net/Zymic/reflect.html