The chaotic rhythms of life

In the 1970s, population biologists helped to launch the theory of chaos. Now it seems that many aspects of life are probably chaotic. But the problem is that they are also difficult to study .

Robert May

ONE of the most memorable museum exhibits I have ever seen is in the Smithsonian Museum of Natural History in Washington DC, where the floor, cupboards and ceiling of a kitchen are covered with the thousands of cockroaches that would be produced by an average female cockroach if all her offspring survived. The exhibit vividly illustrates one of the basic tenets of Darwinian evolution: all animals have the capacity to do more than replace themselves. But most of the time, a variety of factors-predators, limited food supplies, disease and a myriad others-hold the populations in check.

The result is that most populations of plants and animals usually fluctuate. They tend to increase after dropping to unusually low densities (at which point, the conditions become most suitable for maximum growth) and, after reaching unusually high densities, they tend to decrease again. One of the main aims of ecologists is to discover just what the "density-dependent" effects regulating populations are. Such understanding is not only fundamentally important, but it also has practical applications in trying to predict the likely effects of natural or man-made changes such as occur when a population is harvested or when climate patterns alter.

Limits to growth: what stops cockroaches from taking over the Universe?

Until recently, most ecologists assumed that the effects regulating density would, in the absence of other factors, keep a population at some constant level, and that the irregular fluctuations actually seen in so many natural populations resulted from unpredictable ups and downs in various environmental influences. So ecologists studying population dynamics saw their task as trying to extract a steady signal from the masking overlay of environmental noise.

But in the early 1970s, George Oster at the University of California in Berkeley, Jim Yorke at the University of Maryland, I and others began to look more closely at the equations that fish biologists and entomologists had proposed to describe fluctuations in populations. We found that these equations show an extraordinary variety of dynamical behaviour, surprisingly richer than biologists had previously assumed.

Take the equation

x_t+l =lx_t(1 -x_t)

which can describe how a population behaves, and whose rich mathematical character Franco Vivaldi has already discussed in this series ("An experiment with mathematics", 28 October). Here x_t may represent the population of an insect with the subscript t labelling each successive, discrete generation. Suppose that each adult in. generation t would produce l offspring if there is no overcrowding. Then the population of the next generation, x_t be l x_t. The additional factor (1 - x_t ) in the equation represents the feedback from effects due to density or crowding. The population density is scaled such that beyond a crowding level x = 1, it goes to zero (that is, negative values of x correspond to extinction).

Beginning in the early 1970s, these ecological studies have brought this important equation to centre stage in many scientific disciplines. When l is less than 1, the population decreases to zero (for the obvious reason that its reproductive rate is below unity). When l is greater than 1, but less than 3, the population settles to the constant value that intuition would suggest. Further increases in l result in an increasing propensity for the population to "boom" when its density is low, and "bust" when it is high.

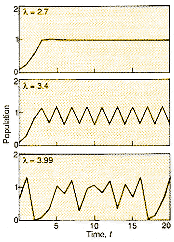Figure 1 Different values of l in our simple equation produce widely differing patterns. In a, the population settles to a constant level; in b, the population alternates between high and low in successive populations; and in c, the population behaves chaotically.

This increasing tendency to "boom and bust" shows up as positive feedback (akin to the shrieks from a microphone when the increase in power level is turned too high) and the population oscillates in a cycle with a period of two generations, alternating between a high and a low value. As l continues to increase beyond 3, these cycles become more complex, with the period lengthening, under successive doublings, to four generations, then eight, then 16, and soon. The population continues, however, to alternate between high and low in successive generations. Finally, when l is bigger than about 3.57, a domain of apparently random fluctuations appears. This is chaos. The simple iterative rule now generates population values that look for all the world like samples from some random process. Figure 1 shows the spectrum of possibilities.

For population biologists, the first message from all this is that the signals from the purely deterministic processes controlling the population density can look like random noise. Even more disconcerting is that, as previous articles in this series have described, in a chaotic system, although the starting values of x might be quite close together, they diverge fairly rapidly, eventually leading to quite different trajectories (see Figure 2). This sensitivity to initial conditions means that long-term prediction is impossible.

Why didn't people recognise earlier these properties of what is a very simple equation? Several mathematicians had unravelled its mathematical characteristics, but failed to realise what they implied for the real world. On the other hand, several ecologists, such as William Ricker who worked on fisheries at the University of British Columbia and P. A. P. Moran who worked on insect populations at the Australian National University in Canberra, had actually studied the equation. They were seeking steady solutions, however, and having found them they conveniently forgot the chaotic behaviour that they had also noticed. What happened in the early 1970s is that ecologists with sufficient mathematical know-how to understand the equations looked at them in practical settings, so grasping their wider implications.

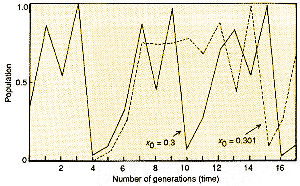Figure 2 shows how sensitive the growth of a population is to the initial conditions when the dynamics are chaotic. Although the initial values for two populations differ only by 0.3 per cent, their trajectories rapidly diverge.

To study the dynamics of a population in the light of such deterministic equations, we must bring our sample species into the laboratory. Here, we can control the environment and eliminate the complicating effects of interactions with other populations. The result is a kind of living computer-useful, but not giving a reliable picture of how the population really behaves in nature, where other species or environmental changes may strongly affect the dynamics.

There have been a few such laboratory studies, using quite small creatures, such as rotifers, Daphnia and blowflies, which have the advantage that they do not take up too much space and their generations tick over fairly fast. By raising the temperature, for instance, the experimenter can speed up metabolic processes so that the fluctuations in population become more pronouncedly "booming and busty". Such studies have, indeed, behaved as expected from the equation. But they do not produce the beautifully crisp period doublings and other phenomena that make the corresponding experiments on physical systems so compelling.

In the natural world, the job of filtering the information that we want-the density-dependent signals-from superimposed environmental noise is hard enough if the underlying dynamics are steady. But if the signal itself is chaotic, the situation is even more complicated. One powerful method for exploring this problem is to create a computer model, which generates sets of artificial "pseudo-data" representing the size of a population, generation by generation.

In this imaginary world, the investigator can specify all the factors governing the population's size. The researchers can then analyse these pseudo-data using the methods normally applied to real data from the field. In this way, they can judge whether the methods do indeed lay bare the mechanisms controlling a population's density that were built into the imaginary world.

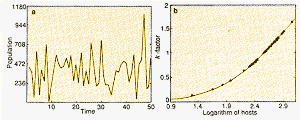Figure 3a The size of an imaginary insect population, year by year, as given by a computer model. The variations are due to a mixture of chaotic dynamics and real noise. Figure 3b: Here, the curve through the points indicates that conventional k-factor analysis can unscramble the signal from the noise, and so detect the effects of insect- population density on the dynamics.

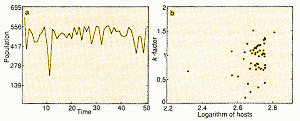Figure 4a is the same as 3a but includes a random factor in the number of eggs laid by an adult insect. Again, there is a mixture of chaotic and genuinely random effects. Figure 4b This time, k-factor analysis just gives a cloud of points. That is, the standard methods of analysis fail to expose the rules governing this imaginary world.

Michael Hassell of Imperial College, London, for example, employs rules that encapsulate his ideas about the factors influencing certain insect populations. In his computer models, adult insects are distributed, according to rules with some random elements, in many patches, say, on leaves, twigs or bushes. These adults lay eggs. The probability of ensuing larvae surviving depends on how crowded they are in each patch; this is the essential density-dependent factor. Surviving larvae mature into the next generation of adults, who then spread out into other patches and begin the whole process anew.

Figure 3a shows one set of such pseudo-data for the overall population, generation by generation. The fluctuations come partly from random elements in the process of dispersal (mimicking a natural situation), and partly as a result of deterministic chaos from density-dependent effects in crowded patches. Figure 3b shows that analysing the data, with a conventional procedure called "k-factor" analysis (which aims to reconstruct the underlying map relating the sizes of populations in successive generations), gives a simple curve that uncovers how the survival of the larvae does depend on their density in each patch.

Now, Figure 4a repeats this exercise, but, here, we introduce environmental randomness into the model by varying the number of eggs laid by each adult(again,the size of these fluctuations accords with real examples . As before, the fluctuations in population sizes from generation to generation come partly from these random factors and partly from deterministic chaos. But applying the same conventional methods to these pseudo-data reveals no discernible signal, as shown in Figure 4b. So, although Hassell knows exactly what governs his world (because he constructed it), the standard techniques fail to show what is really going on. The basic problem is that once patchiness in distribution, environmental noise, and chaotic dynamics all interweave, it can be difficult to disentangle the chaotic, density-dependent signals from additive noise.

Michael Hassell uses computer models to mimic the population dynamics of real insects, such as C. chinensis

There is, unfortunately, no punch line to this part of the story. In the field, chaotic dynamics can create difficulties that we do not fully understand, and which may require more detailed studies than have been usual in the past. Another complication, which Oster and I pointed out in 1976, is that the population we are studying usually interacts with other species,which in turn interact with others, creating a sort of biological many-body problem. Such webs of interactions make chaotic dynamics much more likely. It means that we have to add an extra variable for each species included in the study, resulting in a multi-dimensional system of equations of the kind described in previous articles in this series. So understanding population dynamics then becomes a formidable task.

In these circumstances, William Schaffer at the University of Arizona, Mark Kot at the University of Tennessee, George Sugihara at the Scripps Institution of Oceanography in San Diego, and others, have explored ways of analysing data to see whether the dynamics are truly chaotic. One approach is to look for mathematical indicators of chaos underlying the dynamics, such as a "strange attractor" in multidimensional phase space, as described in Ian Stewart's article two weeks ago ("Portraits of chaos", 4 November). We can then try to construct the attractor-without any understanding of the fundamental biological mechanisms generating it-and set it in the appropriate dimensions to make it "come into focus".

Taking this approach, Schaffer and Kot looked at cases of measles in New York City over a 40-year period. They found that, for example, the string of monthly data, or time series, for the numbers of measles cases from 1928 to 1968 when vaccination began to alter the dynamics of the system-revealed a three-dimensional attractor. So-called "Poincare' cross-sections", or planes slicing across the attractor, suggest that the dynamics correspond to deterministic chaos generated by an approximately one-dimensional map, or an equation of the kind we have already described.

Researchers have analysed these, and other measles data from Copenhagen, using other methods of detecting chaos. In all cases, the conclusion is that deterministic chaos best explains the data, although the length of the time series (at best some 500 monthly points for the New York data) is too short for a truly reliable analysis by these data-hungry techniques.
This approach of distinguishing between chaos and random noise in population biology is in its infancy. Even when successful, such methods tell us only that there are some nonlinear, density-dependent mechanisms operating, but do not tell us what the mechanisms are. To some ecologists this has an air of black magic. But I think the approach is useful. It can show us when it may be profitable to search for such mechanisms and to attempt to make short-term predictions from apparently noisy data.

You might suspect that you could apply similar kinds of mathematical analysis to other areas of biology where feedback might lead to chaotic changes. You would be right. Chaos may be important for understanding some aspects of how genetic variability is maintained in natural populations. You only have to look around you in the street to see that human beings differ a great deal, for example, in height, weight and facial appearance. How is this variability, or polymorphism, generated and maintained in a species? One way is through natural selection that depends on the relative or absolute abundance of individuals with the same genetic makeup, or genotype, in such a way as to favour rarer genotypes. There are many ecological effects that result in a rarer genotype enjoying a selective advantage. As J. B. S. Haldane first emphasised in 1949, the effects of infectious diseases are particularly important because diseases spread more effectively among more crowded populations. If different genotypes of hosts have differing degrees of resistance to different strains of a pathogen, then the rarest genotypes will enjoy a selective advantage. The reason is that the pathogens afflicting them will spread less effectively, or not at all, because the hosts are more spread out.

This is not an oriental emblem but a "map" of a certain kind of predator-prey system. The horizontal axis is the prey population and the vertical axis is the predator population, as they vary together over time. The fluctuating populations are mainly found in the golden region, with occasional oscillations into the larger crimson domain.

Until recently, conventional analyses of population genetics showed that such selective effects could maintain variability within a species, but these static analyses tended to assume that the proportions of the different genotypes remained constant overtime. William Hamilton at Oxford, Simon Levin and David Pimentel at Cornell, Roy Anderson at Imperial College, London, and I have more recently studied the dynamic properties of the interactions among hosts and pathogens. The studies show that the proportions of any one genotype are likely to fluctuate chaotically from generation to generation. Such chaotically fluctuating polymorphisms are likely to be the rule rather than the exception.

So far, few biologists have investigated changes in the proportion of different genotypes present over time in real populations. Karen Forsythe of the Walter and Eliza Hall Institute of Medical Research in Melbourne has shown that the predominant strain of malaria in people in New Guinea differs from village to village, or in the same village over time, in ways that look chaotic. Studies of patchily distributed populations of plants in the Snowy Mountains by Jeremy Burdon of CSIRO in Canberra also give enigmatic hints of chaotic changes in gene frequency.

What is clear is that the selective mechanisms that maintain genetic diversity within populations can do so at chaotically fluctuating levels. There is currently much excitement about sequencing what is called the human genome. Evolutionary biologists have long recognised, however, that understanding variability within human genomes will be just as exciting. Chaos could add an extra dimension to this enterprise.
Given the number of biological and environmental factors likely to influence the dynamics and genetics of natural populations, we might expect to find more unequivocal examples of chaotic dynamics at the sub-organismal level, in physiological or neurobiological processes.

Leon Glass and Michael Mackey at McGill University in Montreal were among the first to explore the possibility that many medical problems may be what they call "dynamical diseases", produced by changes in physiological factors that cause normally rhythmic processes to show erratic or chaotic fluctuations. For instance, in some blood diseases the numbers of blood cells show large oscillations that are not normally present. Glass and Mackey showed that simple, but realistic, mathematical models for controlling blood cell production display the same periodic and chaotic oscillations as seen clinically when some parameter is varied. Such changes in the parameters of the model have a physiological interpretation. Clifford Gurney of the University of Chicago has performed experiments, based on Mackey and Glass's models, which produce oscillations in numbers of blood cells in mice.

Breakdowns in cardiac rhythms are obvious candidates for "dynamical diseases". The best studies of the dynamics of heartbeats, however, come from Petri dishes, not humans. Glass and his colleagues, Michael Guevara and Alvin Shrier, showed that a cluster of heart cells from chick embryos will beat spontaneously with an innate and regular rhythm. Applying a strong electric field to this cell aggregate resets the phase of the heartbeat; that is, the next beat will be earlier or later than normal. Introducing a periodic series of such electrical impulses means that the heart is pushed by two forces with different periods: one with the heart cells' intrinsic rhythm and the other with the rhythm of the electrical shocks. The ensuing heartbeat depends on the relation between these two periods.

In some cases, the heart cells resonate with some harmonic of the stimulus, beating once for each jolt, or twice, or perhaps three times for each two jolts, and so on. In other instances, the cells fire apparently at random, giving irregular or chaotic patterns. Glass and his colleagues interpret the dynamics of these periodic or chaotic patterns in terms of the complex bifurcations that result from the interplay between the innate physiological rhythms of heart cells and the frequency of the forcing electrical stimuli. These experiments show that you can induce and study chaos in an artificial system that is a metaphor for cardiac processes. Applying these to cardiac arrhythmias, or to electrocardiograms before and after heart attacks, is, however, still at an early stage.

Neurophysiology also offers a wide range of phenomena that are candidates for "dynamical diseases", or abnormal oscillations and complex rhythms posing therapeutic problems. Sometimes, there is a marked oscillation in a neurological control system that does not normally have a rhythm. Examples are ankle tremor in patients with corticospinal tract disease, various movement disorders (Parkinson's tremors, for instance), and the abnormal paroxysmal oscillations in the discharge of neurons that occur in many seizures.

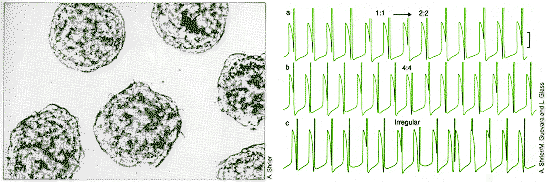Periodic electrical shocks applied to spontaneously beating heart cells from chick embryos (left) can cause the heartbeat to undergo period doubling, as in traces a and b. In trace c, the electrical stimulus produces a chaotic heartbeat.

Alternatively, there can be qualitative changes in the oscillations within an already rhythmic process, as in abnormalities in walking, altered sleep-wake cycles, or rapidly cycling manic depression. Yet again, clinical events may recur in seemingly random fashion, as in seizures in adult epileptics. Neural processes are, however, so complex that it is not easy to see how models for these dynamical diseases-if, indeed, they exist,can be developed, tested and understood.

One approach, taken by Paul Rapp at the College of Medicine of the State University of Pennsylvania, rests on analysing the dynamical complexity of electroencephalograms (EEGs) which recorded the patterns of brain activity of human subjects as they performed various tasks. Rapp found that the complexity of the patterns changed in response to changes in intellectual effort. One study, for example, asked subjects to count backwards from 700 by sevens. Rapp characterised the changing complexity of the resulting EEG patterns using what is becoming a standard method for analysing chaotic rhythmic processes; he computed the fractal dimension of the jagged time series, and found the dimension rose from its background value of around 2.3 to around 2.9 during the tests. He infers that the higher-dimensional, more complicated EEG patterns correspond to a more alert state.

If we want to understand the dynamics of neurophysiological processes more clearly, we need a simpler system that we can control, such as the light reflex of the pupil of the eye. This reflex is a neural control mechanism with a delayed negative feedback, which regulates the amount of light reaching the retina by changing the area of the pupil. You can see the phenomenon informally by playing with a torch in front of a mirror. If you want to publish in a scientific journal, however, you would do better to control the observations by "clamping" the pupil light reflex; the feedback loop is first "opened" by focusing a light beam onto the centre of the pupil; the loop is then "closed" by an electronically constructed circuit, or "clamping box", which relates measured changes in pupil area to changes in the light shed on the retina. The time delay in the pupil's response, or "pupil latency", is around 0.3 seconds. As the gain and/or delay in the feedback loop increases, the pupil light-reflex becomes unstable and starts to oscillate periodically. In another experiment, where Andre Longtin, John Milton and colleagues (also at McGill), designed the clamping box to mimic mixed" feedback, the pupil reflex became unstable and produced aperiodic oscillations. This is due to the interaction of complex, possibly chaotic, dynamics and neural noise.

These physiological and neurological studies are reminiscent of those on single populations of animals, in that it is hard to apply theory to the real situation. Theory and experiment do agree, with varying degrees of precision, in the laboratory, but these simple, artificial demonstrations are always open to the cavil that they are no more than animated computer experiments. Many evolutionary biologists think that chaotic dynamics do not exist among real populations, because the accompanying fluctuations carry the risk that subpopulations will wink out, patch by patch, rendering long-term persistence unlikely. By the same token, earlier work tends to see chaos as a villain in physiology, manifesting itself in "dynamically diseased" arrhythmias or seizures.

Ary Goldberger at Harvard Medical School has argued, to the contrary, that chaos gives the human body the flexibility to respond to different kinds of stimuli, and in particular that the rhythms of a healthy heart are chaotic. Goldberger bases his claims on analyses of electrocardiograms of normal individuals and heart-attack patients. He argues that healthy people have ECGs with complex irregularities, which vary systematically on timescales from seconds to days, whereas people about to experience a heart attack have much simpler heart rhythms. Critics correctly observe, however, that the broad patterns do not necessarily imply chaos, and that more emphasis should be put on studying the dynamics of heartbeats and the physical performance of the heart.

On an even more speculative note, Alisdair Houston at Oxford has pointed out that there is one context where chaotic unpredictability certainly could be useful. Organisms seeking to evade a pursuing predator would benefit from unpredictable patterns of flight behaviour. I believe it likely that many organisms have evolved simple behavioural rules that generate chaotically unpredictable patterns of evading predators.

One thing is certain. Biological systems, from communities and populations to physiological processes, are governed by nonlinear mechanisms. This means that we must expect to see chaos as often as we see cycles or steadiness. The message that I urged more than 10 years ago is even more true today: "not only in [biological] research, but also in the everyday world of politics and economics, we would all be better off if more people realised that simple nonlinear systems do not necessarily possess simple dynamical properties."

Robert May is a Royal Society Research Professor in the zoology department at the University of Oxford and at Imperial College London. Moving from theoretical physics, he is now interested in the dynamics of biological populations, ranging from the structure and diversity of communities of interacting species to the behaviour of insect populations and the epidemiology of HIV-AIDS.

MAIN INDEX
REFERENCE GUIDE			TRANSCRIPTS				GLOSSARY
Chaos	Quantum	Logic	Cosmos	Conscious	Belief	Elect.	Art	Chem.	Maths